2.6 非Transformer架构

Transformer结构是当前大语言模型的主流模型架构，其具备构建灵活、易并行、易扩展等优势。但是，Transformer也并非完美。其并行输入的机制会导致模型规模随输入序列长度平方增长，导致其在处理长序列时面临计算瓶颈。为了提高计算效率和性能，解决Transformer在长序列处理中的瓶颈问题，可以选择基于RNN的语言模型。RNN在生成输出时，只考虑之前的隐藏状态和当前输入，理论上可以处理无限长的序列。然而，传统的RNN模型（如GRU、LSTM等）在处理长序列时可能难以捕捉到长期依赖关系，且面临着梯度消失或爆炸问题。为了克服这些问题，近年来，研究者提出了两类现代RNN变体，分别为状态空间模型（State Space Model，SSM）和测试时训练（Test-Time Training，TTT）。这两种范式都可

以实现关于序列长度的线性时间复杂度，且避免了传统 RNN 中存在的问题。本节将对这两种范式及对应的代表性模型进行简要介绍。

2.6.1 状态空间模型SSM

状态空间模型（State Space Model，SSM）[13]范式可以有效处理长文本中存在的长程依赖性（Long-Range Dependencies, LRDs）问题，并且可以有效降低语言模型的计算和内存开销。本小节将首先介绍SSM范式，再分别介绍两种基于SSM范式的代表性模型：RWKV和Mamba。

1. SSM

SSM 的思想源自于控制理论中的动力系统。其通过利用一组状态变量来捕捉系统状态随时间的连续变化，这种连续时间的表示方法天然地适用于描述长时间范围内的依赖关系。此外，SSM 还具有递归和卷积的离散化表示形式，既能在推理时通过递归更新高效处理序列数据，又能在训练时通过卷积操作捕捉全局依赖关系。

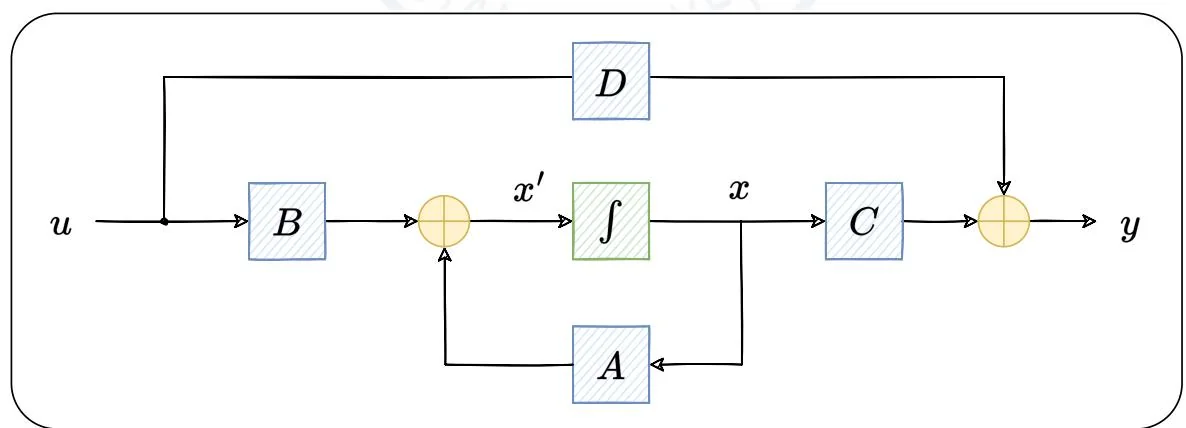
图2.17：SSM范式。

如图2.17，SSM在三个随时间 $t$ 变化的变量和四个可学习的矩阵的基础上构造而成。三个变量分别为： $x(t)\in \mathbb{C}^n$ 表示 $n$ 个状态变量， $u(t)\in \mathbb{C}^{m}$ 表示 $m$ 个状

态输入, $y(t) \in \mathbb{C}^{p}$ 表示 $p$ 个输出。四个矩阵分别为: 状态矩阵 $\mathbf{A} \in \mathbb{C}^{n \times n}$ , 控制矩阵 $\mathbf{B} \in \mathbb{C}^{n \times m}$ , 输出矩阵 $\mathbf{C} \in \mathbb{C}^{p \times n}$ 和命令矩阵 $\mathbf{D} \in \mathbb{C}^{p \times m}$ 。SSM 的系统方程为:

x ^ {\prime} (t) = \mathbf {A} x (t) + \mathbf {B} u (t) \tag {2.5}

y (t) = \mathbf {C} x (t) + \mathbf {D} u (t),

其中， $x'(t) = \mathbf{A}x(t) + \mathbf{B}u(t)$ 为状态方程，描述了系统状态如何基于输入和前一个状态变化，其计算出的是状态关于时间的导数 $x'(t)$ ，为了得到状态 $x(t)$ ，还需对其进行积分操作。 $y(t) = \mathbf{C}x(t) + \mathbf{D}u(t)$ 为输出方程，描述了系统状态如何转化为输出，其中的 $x(t)$ 是通过状态方程更新且积分后的值。在深度学习中， $\mathbf{D}u(t)$ 项表示残差连接，可被忽略。

该方程可视作SSM系统方程的连续形式，适用于对连续数据（例如音频信号、时间序列）的处理，但是在训练和推理都非常慢。为了提高对SSM的处理效率，需要对该方程进行离散化操作。离散化（Discretization）是SSM中最为关键的步骤，能够将系统方程从连续形式转换为递归形式和卷积形式，从而提升整个SSM架构的效率。将连续形式的SSM系统方程离散化时，可以使用梯形法代替连续形式中的积分操作，其原理是将定义在特定区间上的函数曲线下的区域视为梯形，并利用梯形面积公式计算其面积。由此，可以得出离散化后递归形式下的系统方程：

x _ {k} = \bar {\mathbf {A}} x _ {k - 1} + \bar {\mathbf {B}} u _ {k} \tag {2.6}

y _ {k} = \bar {\mathbf {C}} x _ {k} 。

在该方程中，状态方程由前一步的状态和当前输入计算当前状态，体现了递归的思想。其中， $\bar{\mathbf{A}}, \bar{\mathbf{B}}, \bar{\mathbf{C}}$ 为离散形式下的矩阵，其与连续形式下矩阵 $\mathbf{A}, \mathbf{B}, \mathbf{C}$ 的关系分别表示为： $\bar{\mathbf{A}} = \left(\mathbf{I} - \frac{\Delta}{2}\mathbf{A}\right)^{-1}\left(\mathbf{I} + \frac{\Delta}{2}\mathbf{A}\right)$ ， $\bar{\mathbf{B}} = \left(\mathbf{I} - \frac{\Delta}{2}\mathbf{A}\right)^{-1}\Delta \mathbf{B}$ ， $\bar{\mathbf{C}} = \mathbf{C}$ ，其中 $\Delta = t_{n+1} - t_n$ 。

递归形式的SSM类似于RNN，具有RNN的优缺点。其适用于顺序数据的处理，能够实现与序列长度呈线性复杂度的高效推理，但是无法并行训练，当面临长

序列时存在梯度消失或爆炸问题。将系统方程的递归形式进行迭代，可以得到卷积形式。这里省略了推导过程，直接给出迭代后 $x_{k}$ 和 $y_{k}$ 的结果：

x _ {k} = \bar {\mathbf {A}} ^ {k} \bar {\mathbf {B}} u _ {0} + \bar {\mathbf {A}} ^ {k - 1} \bar {\mathbf {B}} u _ {1} + \dots + \bar {\mathbf {B}} u _ {k} \tag {2.7}

y _ {k} = \bar {\mathbf {C}} x _ {k} = \bar {\mathbf {C}} \bar {\mathbf {A}} ^ {k} \bar {\mathbf {B}} u _ {0} + \bar {\mathbf {C}} \bar {\mathbf {A}} ^ {k - 1} \bar {\mathbf {B}} u _ {1} + \dots + \bar {\mathbf {C}} \bar {\mathbf {B}} u _ {k} \circ

可以观察到，将系统方程的递归形式迭代展开后，输出 $y_{k}$ 是状态输入 $u_{k}$ 的卷积结果，其卷积核为：

\bar {\mathbf {K}} _ {k} = \left(\bar {\mathbf {C}} \bar {\mathbf {B}}, \bar {\mathbf {C}} \bar {\mathbf {A}} \bar {\mathbf {B}}, \dots , \bar {\mathbf {C}} \bar {\mathbf {A}} ^ {k} \bar {\mathbf {B}}\right) 。 \tag {2.8}

因此，SSM系统方程的卷积形式为：

y _ {k} = \bar {\mathbf {K}} _ {k} * u _ {k}, \tag {2.9}

其中，卷积核是由SSM中的矩阵参数决定的，由于这些参数在整个序列的处理过程中是固定的，被称为时不变性。时不变性使得SSM能够一致地处理不同时间步长的数据，进行高效的并行化训练。但由于上下文长度固定，卷积形式的SSM在进行自回归任务时延迟长且计算消耗大。结合离散化后SSM的递归形式和卷积形式的优缺点，可以选择在训练时使用卷积形式，推理时使用递归形式。

综上，SSM架构的系统方程具有三种形式，分别为连续形式、离散化的递归形式以及离散化的卷积形式，可应用于文本、视觉、音频和时间序列等任务，在应用时，需要根据具体情况选择合适的表示形式。SSM的优势在于能够处理非常长的序列，虽然比其它模型参数更少，但在处理长序列时仍然可以保持较快的速度。

当前，各种现有SSM架构之间的主要区别在于基本SSM方程的离散化方式或A矩阵的定义。例如，S4[14]（Structured State Space Model）是一种SSM变体，其关键创新是使用HiPPO矩阵来初始化A矩阵，在处理长序列数据时表现优异。此外，RWKV和Mamba是两种基于SSM范式的经典架构，下面将分别介绍这两种架构。

2. RWKV

RWKV（Receptance Weighted Key Value）[26]是基于SSM范式的创新架构，其核心机制WKV的计算可以看作是两个SSM的比。RWKV的设计结合了RNNs和Transformers的优点，既保留了推理阶段的高效性，又实现了训练阶段的并行化。（注：这里讨论的是RWKV-v4)

RWKV 模型的核心模块有两个：时间混合模块和通道混合模块。时间混合模块主要处理序列中不同时间步之间的关系，通道混合模块则关注同一时间步内不同特征通道30之间的交互。时间混合模块和通道混合模块的设计基于四个基本元素：接收向量 R、键向量 K、值向量 V 和权重 W，下面将根据图 2.18，介绍这些元素在两个模块中的计算流程和作用。

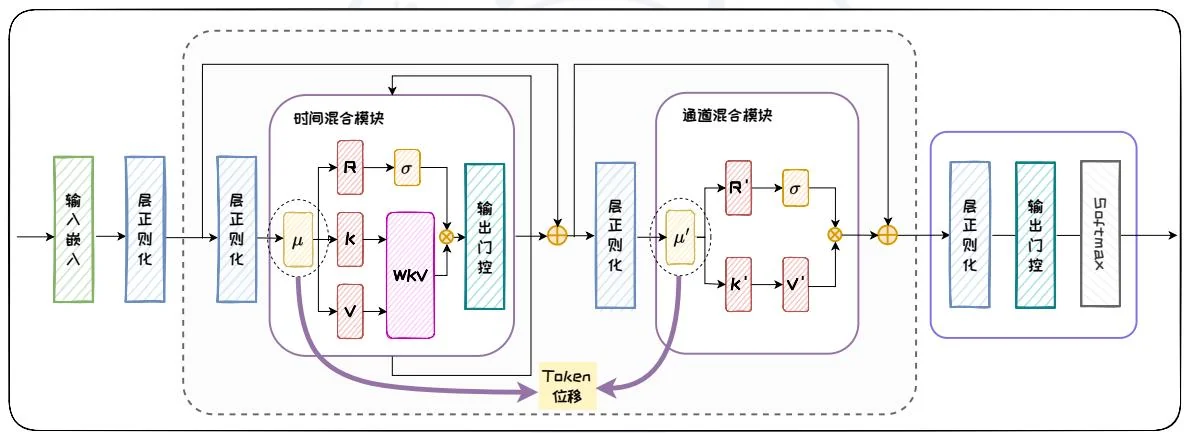
图2.18: RWKV架构。

时间混合模块和通道混合模块中共有的操作是 Token 位移，该步通过对当前时间步和前一时间步的输入进行线性插值来实现，从而确保了模型对序列中时间变化的敏感性。在时间混合模块中，接受向量 R 负责接收并整合来自序列历史的信息，权重 W 表示位置权重衰减，键向量 K 和值向量 V 类似传统注意力机制中的键和值，分别用于匹配和携带信息。时间混合模块首先将当前步长和前一步长的

输入进行线性组合，通过线性投影得到 R、K、V 向量；随后，通过 WKV 机制来确保每个通道的权重随时间推移逐步衰减；最后，将表示过去信息的 $\sigma(\mathbf{R})$ 和表示当前信息的 WKV 向量通过输出门控进行整合，传递给通道混合模块。

时间混合模块中的WKV机制是RWKV的核心部分。在RWKV中，权重W是一个与通道相关的时间衰减向量，该向量可以表示为： $w_{t,i} = -(t - i)w$ ， $i$ 表示从当前时间步长 $t$ 向后追溯的某个时间步长， $w$ 是一个非负向量，其长度为通道数。通过这种方式，模型能够捕捉时间序列中不同时间步长之间的依赖关系，实现每个通道权重随时间向后逐步衰减的效果。WKV机制的关键在于利用线性时不变递归来更新隐藏状态，这可以看作是两个SSM之比。具体公式为：

w k v _ {t} = \frac {\sum_ {i = 1} ^ {t - 1} e ^ {- (t - 1 - i) w + k _ {i}} \odot v _ {i} + e ^ {u + k _ {t}} \odot v _ {t}}{\sum_ {i = 1} ^ {t - 1} e ^ {- (t - 1 - i) w + k _ {i}} + e ^ {u + k _ {t}}}, \tag {2.10}

其中， $u$ 是一个单独关注当前 Token 的向量。由于分子和分母都表现出状态更新和输出的过程，与 SSM 思想类似，因此该公式可以看作是两个 SSM 之比。通过权重 W 和 WKV 机制，模块能够有效地处理长时间序列数据，并减少梯度消失问题。

在通道混合模块中， $\mathbf{R}^{\prime}$ 、 $\mathbf{K}^{\prime}$ 、 $\mathbf{V}^{\prime}$ 的作用与时间混合模块类似， $\mathbf{R}^{\prime}$ 和 $\mathbf{K}^{\prime}$ 同样由输入的线性投影得到， $\mathbf{V}^{\prime}$ 的更新则额外依赖于 $\mathbf{K}^{\prime}$ 。之后，将 $\sigma(\mathbf{R}^{\prime})$ 和 $\mathbf{V}^{\prime}$ 整合，以实现不同通道之间的信息交互和融合。

此外，RWKV架构还采用了时间依赖的Softmax操作，提高数值稳定性和梯度传播效率，以及采用层归一化来稳定梯度，防止梯度消失和爆炸。为了进一步提升性能，RWKV还采用了自定义CUDA内核、小值初始化嵌入以及自定义初始化等优化措施。

RWKV在模型规模、计算效率和模型性能方面都表现可观。在模型规模方面，RWKV模型参数扩展到了14B，是第一个可扩展到数百亿参数的非Transformer架构。在计算效率方面，RWKV允许模型被表示为Transformer或RNN，从而使得模型在训练时可以并行化计算，在推理时保持恒定的计算和内存复杂度。在模型性

能方面，RWKV在NLP任务上的性能与类似规模的Transformer相当，在长上下文基准测试中的性能仅次于S4。

RWKV 通过创新的线性注意力机制，成功结合了 Transformer 和 RNN 的优势，在模型规模和性能方面取得了显著进展。然而，在处理长距离依赖关系和复杂任务时，RWKV 仍面临一些局限性。为了解决这些问题并进一步提升长序列建模能力，研究者们提出了 Mamba 架构。

3. Mamba

时不变性使得SSM能够一致地处理不同时间步长的数据，进行高效的并行化训练，但是同时也导致其处理信息密集的数据（如文本）的能力较弱。为了弥补这一不足，Mamba[12]基于SSM架构，提出了选择机制（Selection Mechanism）和硬件感知算法（Hardware-aware Algorithm），前者使模型执行基于内容的推理，后者实现了在GPU上的高效计算，从而同时保证了快速训练和推理、高质量数据生成以及长序列处理能力。

Mamba的选择机制通过动态调整模型参数来选择需要关注的信息，使模型参数能够根据输入数据动态变化。具体来说，Mamba将离散化SSM中的参数B,C, $\Delta$ 分别转变成以下函数： $s_{\mathbf{B}}(x) = \mathrm{Linear}_N(x)$ 、 $s_{\mathbf{C}}(x) = \mathrm{Linear}_N(x)$ 、 $s_{\Delta}(x) =$ BroadcastD(Linear1(x))，并采用非线性激活函数 $\tau_{\Delta} =$ softplus来调节参数 $\Delta$ 。其中Lineard是对特征维数 $d$ 的参数化投影， $s_\Delta$ 和 $\tau_{\Delta}$ 函数的选择与RNN的门控机制相关联[38]。此外，Mamba还对张量形状进行相应调整，使模型参数具有时间维度，这意味着模型参数矩阵在每个时间步都有不同的值，从时间不变转变为时间变化的。

选择机制使模型参数变成了输入的函数，且具有时间维度，因此模型不再具备卷积操作的平移不变性和线性时不变性，从而影响其效率。为了实现选择性SSM模型在GPU上的高效计算，Mamba提出一种硬件感知算法，主要包括内核融合、

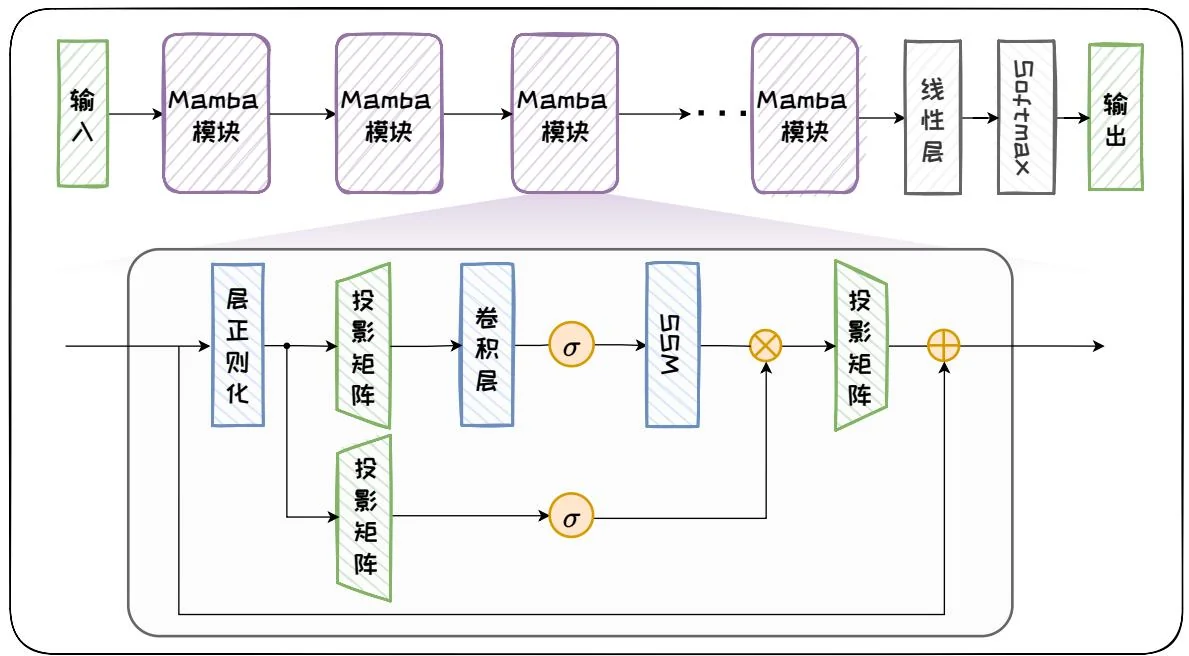
图2.19:Mamba架构。

并行扫描和重计算三方面内容。内核融合通过减少内存 I/O 操作来提高速度。并行扫描利用并行化算法提高效率。重计算则在反向传播时重新计算中间状态，以减少内存需求。

具体实现中，将SSM参数从较慢的高带宽内存（HBM）加载到更快的静态随机存取存储器（SRAM）中进行计算，然后将最终输出写回HBM。这样可以在保持高效计算的同时，减少内存使用，使模型内存需求与优化的Transformer实现（如FlashAttention）相同。

Mamba 通过将带有选择机制的 SSM 模块与 Transformer 的前馈层相结合, 形成了一个简单且同质的架构设计。如图 2.19 所示, Mamba 架构是由完全相同的 Mamba 模块组成的递归模型, 每个 Mamba 模块都在前馈层中插入了卷积层和带有选择机制的 SSM 模块, 其中激活函数 $\sigma$ 选用 SiLU/Swish 激活。

通过引入选择机制和硬件感知算法，Mamba在实际应用中展示了卓越的性能和效率，包括：（1）快速训练和推理：训练时，计算和内存需求随着序列长度线性增长，而推理时，每一步只需常数时间，不需要保存之前的所有信息。通过硬件

感知算法，Mamba 不仅在理论上实现了序列长度的线性扩展，而且在 A100 GPU 上，其推理吞吐量比类似规模的 Transformer 提高了 5 倍。（2）高质量数据生成：在语言建模、基因组学、音频、合成任务等多个模态和设置上，Mamba 均表现出色。在语言建模方面，Mamba-3B 模型在预训练和后续评估中性能超过了两倍参数量的 Transformer 模型性能。（3）长序列处理能力：Mamba 能够处理长达百万级别的序列长度，展示了处理长上下文时的优越性。

虽然 Mamba 在硬件依赖性和模型复杂度上存在一定的局限性，但是它通过引入选择机制和硬件感知算法显著提高了处理长序列和信息密集数据的效率，展示了在多个领域应用的巨大潜力。Mamba 在多种应用上的出色表现，使其成为一种理想的通用基础模型。

2.6.2 训练时更新 TTT

在处理长上下文序列时，上述基于SSM范式的架构（例如RWKV和Mamba）通过将上下文信息压缩到固定长度的隐藏状态中，成功将计算复杂度降低至线性级别，有效扩展了模型处理长上下文的能力。然而，随着上下文长度的持续增长，基于SSM范式的模型可能会过早出现性能饱和。例如，Mamba在上下文长度超过16k时，困惑度基本不再下降[37]。出现这一现象的原因可能是固定长度的隐藏状态限制了模型的表达能力，同时在压缩过程中可能会导致关键信息的遗忘。

为了解决这一限制，测试时训练（Test-Time Training，TTT）[37]范式提供了一种有效的解决方案。TTT利用模型本身的参数来存储隐藏状态、记忆上文；并在每一步推理中，对模型参数进行梯度更新，已实现上文的不断循环流入，如图2.20所示。这个过程不同于传统的机器学习范式中模型在完成训练后的推理阶段通常保持静态的方式，TTT在推理阶段会针对每一条测试数据一边循环训练一边推理。为了实现这种测试时训练的机制，TTT在预训练和推理阶段均进行了独特的设计。

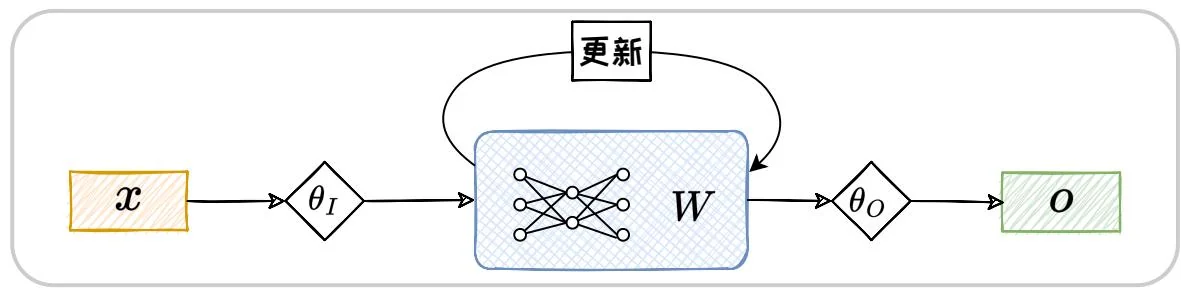
图2.20：TTT范式下的推理流程。

在 TTT 范式的预训练阶段，训练过程包含内部循环以及外部循环两个部分。其中外部循环遵循传统的下词预测任务，通过自回归方式优化模型全局权重参数。内部循环则是基于自监督的方式来优化隐藏状态。具体来说，模型需要在每个时间步动态地更新隐藏状态，使其能够不断适应新的输入数据。这种动态更新的机制类似于一个独立的机器学习模型在每个时间步对输入进行训练和优化。给定当前时间步输入 $x_{t}$ 以及先前历史上下文 $x_{1}, x_{2}, \ldots, x_{t-1}$ 对应的隐藏状态 $W_{t-1}$ ，模型计算当前时间步的重构损失：

\ell \left(W _ {t - 1}; x _ {t}\right) = \left\| f \left(\theta_ {K} x _ {t}; W _ {t - 1}\right) - \theta_ {V} x _ {t} \right\| ^ {2}, \tag {2.11}

其中 $\theta_{K}$ 和 $\theta_{V}$ 是通过外部循环学习到的参数。接着, 模型以学习率 $\eta$ 利用该损失进行梯度下降, 更新隐藏状态:

W _ {t} = W _ {t - 1} - \eta \nabla \ell \left(W _ {t - 1}; x _ {t}\right) 。 \tag {2.12}

最终，模型基于更新后的隐藏状态和当前输入生成输出：

z _ {t} = f \left(x _ {t}; W _ {t}\right) 。 \tag {2.13}

在推理阶段，无需执行外部循环任务。因此，模型只进行内部循环来对隐藏状态进行更新，使模型更好地适应新的数据分布，从而提升预测性能。

与Transformer相比，基于TTT范式的模型具有线性时间复杂度，这对于处理长序列数据至关重要。相较于基于SSM的RWKV和Mamba架构，TTT通过模型

参数来保存上下文信息，能够更有效地捕捉超长上下文中的语义联系和结构信息。因此，TTT在长上下文建模任务中展现出卓越的性能，特别是在需要处理超长上下文的应用场景中。未来，TTT范式有望在超长序列处理任务中发挥重要作用。

参考文献

[1] Joshua Ainslie et al. “Gqa: Training generalized multi-query transformer models from multi-head checkpoints”. In: arXiv preprint arXiv:2305.13245 (2023).
[2] Rohan Anil et al. “Palm 2 technical report”. In: arXiv preprint arXiv:2305.10403 (2023).
[3] Tim Bayne and Iwan Williams. “The Turing test is not a good benchmark for thought in LLMs”. In: Nature Human Behaviour 7.11 (2023), pp. 1806–1807.
[4] Sid Black et al. “Gpt-neox-20b: An open-source autoregressive language model”. In: arXiv preprint arXiv:2204.06745 (2022).
[5] Tom Brown et al. "Language models are few-shot learners". In: NeurIPS. 2020.
[6] Mark Chen et al. “Evaluating large language models trained on code”. In: arXiv preprint arXiv:2107.03374 (2021).
[7] Aakanksha Chowdhery et al. “Palm: Scaling language modeling with pathways”. In: Journal of Machine Learning Research 24.240 (2023), pp. 1-113.
[8] Hyung Won Chung et al. “Scaling instruction-finetuned language models”. In: Journal of Machine Learning Research 25.70 (2024), pp. 1-53.
[9] Kevin Clark et al. "Electra: Pre-training text encoders as discriminators rather than generators". In: arXiv preprint arXiv:2003.10555 (2020).
[10] Tim Dettmers et al. “Qlora: Efficient finetuning of quantized llms”. In: NeurIPS. 2024.
[11] Jacob Devlin et al. “BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding”. In: NAACL. 2019.
[12] Albert Gu and Tri Dao. “Mamba: Linear-Time Sequence Modeling with Selective State Spaces”. In: arXiv preprint arXiv:2312.00752 (2023).
[13] Albert Gu, Karan Goel, and Christopher Ré. "Efficiently modeling long sequences with structured state spaces". In: arXiv preprint arXiv:2111.00396 (2021).

[14] Albert Gu et al. "On the Parameterization and Initialization of Diagonal State Space Models". In: NeurIPS. 2022.
[15] Jordan Hoffmann et al. “Training compute-optimal large language models”. In: arXiv preprint arXiv:2203.15556 (2022).
[16] Jared Kaplan et al. "Scaling laws for neural language models". In: arXiv preprint arXiv:2001.08361 (2020).
[17] Zhenzhong Lan et al. “Albert: A lite bert for self-supervised learning of language representations”. In: arXiv preprint arXiv:1909.11942 (2019).
[18] Mike Lewis et al. “Bart: Denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension”. In: ACL. 2020.
[19] Haotian Liu et al. "Visual instruction tuning". In: NeurIPS. 2024.
[20] Qi Liu, Matt J Kusner, and Phil Blunsom. “A survey on contextual embeddings”. In: arXiv preprint arXiv:2003.07278 (2020).
[21] Tiedong Liu and Bryan Kian Hsiang Low. “Goat: Fine-tuned llama outperforms gpt-4 on arithmetic tasks”. In: arXiv preprint arXiv:2305.14201 (2023).
[22] Yinhan Liu et al. “Multilingual denoising pre-training for neural machine translation”. In: Transactions of the Association for Computational Linguistics 8 (2020), pp. 726–742.
[23] Yinhan Liu et al. "Roberta: A robustly optimized bert pretraining approach". In: arXiv preprint arXiv:1907.11692 (2019).
[24] Ha-Thanh Nguyen. “A brief report on lawgpt 1.0: A virtual legal assistant based on gpt-3”. In: arXiv preprint arXiv:2302.05729 (2023).
[25] Long Ouyang et al. "Training language models to follow instructions with human feedback". In: NeurIPS. 2022.
[26] Bo Peng et al. “RWKV: Reinventing RNNs for the Transformer Era”. In: EMNLP. 2023.
[27] Alec Radford et al. "Improving language understanding by generative pre-training". In: (2018).
[28] Rafael Rafailov et al. “Direct preference optimization: Your language model is secretly a reward model”. In: NeurIPS. 2024.

[29] Colin Raffel et al. “Exploring the limits of transfer learning with a unified text-to-text transformer”. In: Journal of machine learning research 21.140 (2020), pp. 1–67.
[30] Baptiste Roziere et al. "Code llama: Open foundation models for code". In: arXiv preprint arXiv:2308.12950 (2023).
[31] Victor Sanh et al. "Multitask prompted training enables zero-shot task generalization". In: arXiv preprint arXiv:2110.08207 (2021).
[32] Ryan Schaeffer, Brando Miranda, and Sanmi Koyejo. "Are emergent abilities of large language models a mirage?" In: NeurIPS. 2024.
[33] John Schulman et al. "Proximal policy optimization algorithms". In: arXiv preprint arXiv:1707.06347 (2017).
[34] Noam Shazeer. “Glu variants improve transformer”. In: arXiv preprint arXiv:2002.05202 (2020).
[35] Shaden Smith et al. "Using deepspeed and megatron to train megatron-turing nlg 530b, a large-scale generative language model". In: arXiv preprint arXiv:2201.11990 (2022).
[36] Jianlin Su et al. “Roformer: Enhanced transformer with rotary position embedding”. In: arXiv preprint arXiv:2104.09864 (2021).
[37] Yu Sun et al. "Learning to (Learn at Test Time): RNNs with Expressive Hidden States". In: arXiv preprint arXiv:2407.04620 (2024).
[38] Corentin Tallec and Yann Ollivier. “Can recurrent neural networks warp time?” In: ICLR. 2018.
[39] Hugo Touvron et al. “Llama 2: Open foundation and fine-tuned chat models”. In: arXiv preprint arXiv:2307.09288 (2023).
[40] Hugo Touvron et al. “Llama: Open and efficient foundation language models”. In: arXiv preprint arXiv:2302.13971 (2023).
[41] Trieu H Trinh and Quoc V Le. “A simple method for commonsense reasoning”. In: arXiv preprint arXiv:1806.02847 (2018).
[42] Ashish Vaswani et al. "Attention is all you need". In: NeurIPS. 2017.
[43] Linting Xue et al. "mT5: A massively multilingual pre-trained text-to-text transformer". In: NAACL. 2021.

[44] Aiyuan Yang et al. “Baichuan 2: Open large-scale language models”. In: arXiv preprint arXiv:2309.10305 (2023).
[45] Deyao Zhu et al. “Minigpt-4: Enhancing vision-language understanding with advanced large language models”. In: arXiv preprint arXiv:2304.10592 (2023).
[46] Yukun Zhu et al. "Aligning books and movies: Towards story-like visual explanations by watching movies and reading books". In: ICCV. 2015.

3 Prompt 工程

随着模型训练数据规模和参数数量的持续增长，大语言模型突破了泛化瓶颈，并涌现出了强大的指令跟随能力。泛化能力的增强使得模型能够处理和理解多种未知任务，而指令跟随能力的提升则确保了模型能够准确响应人类的指令。两种能力的结合，使得我们能够通过精心编写的指令输入，即 Prompt，来引导模型适应各种下游任务，从而避免了传统微调方法所带来的高昂计算成本。Prompt 工程，作为一门专注于如何编写这些有效指令的技术，成为了连接模型与任务需求之间的桥梁。它不仅要求对模型有深入的理解，还需要对任务目标有精准的把握。通过 Prompt 工程，我们能够最大化地发挥大语言模型的潜力，使其在多样化的应用场景中发挥出卓越的性能。本章将深入探讨 Prompt 工程的概念、方法及作用，并介绍上下文学习、思维链等技术，以及 Prompt 工程的相关应用。

2.6_非Transformer架构