5.3 附加参数法：T-Patcher

附加参数法在模型中引入额外的参数，并对这部分参数进行训练以实现特定知识的编辑。其在准确性、泛化性、可迁移性等方面均取得良好的表现。T-Patcher是附加参数法中的代表性方法，其在模型最后一个Transformer层的全连接前馈层中添加额外参数（称为“补丁”），然后对补丁进行训练来完成特定知识的编辑，如图5.9。T-Patcher可以在不改变原始模型整体架构的情况下，对模型进行编辑。本节将从补丁的位置、补丁的形式以及补丁的实现三个方面对T-Patcher展开介绍。

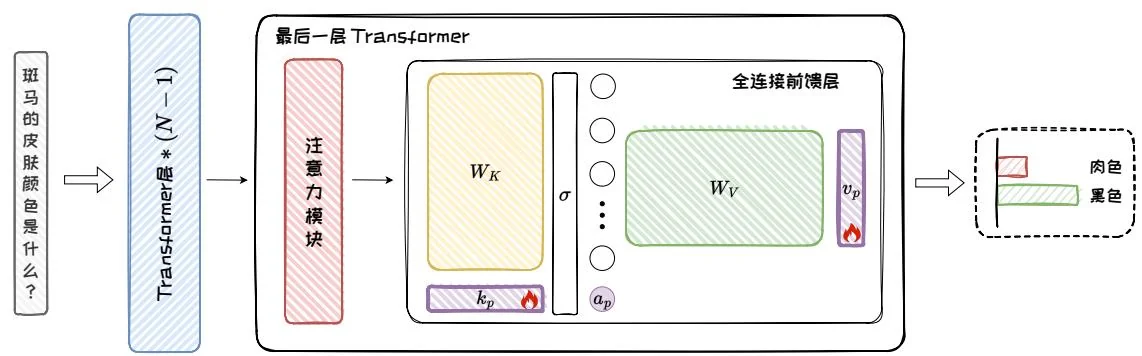
图5.9：T-Patcher方法(图中紫色图块为补丁)。

5.3.1 补丁的位置

将补丁添加在模型中的不同位置会影响模型编辑的效果。T-Patcher 将全连接前馈层视为键值存储体，并选择在最后一个 Transformer 层的全连接前馈层中添加补丁参数。在这种设计中，添加补丁相当于向键值存储体中增加新的记忆单元，通过精确控制补丁的激活，T-Patcher 能够针对特定输入进行修正，并减少对无关输入的影响。此外，由于全连接前馈层结构简单，因此只需要添加少量参数即可实现有效编辑。

图5.10：键值存储体(省略激活函数)。

具体而言，T-Patcher将全连接前馈层视为如图5.10所示的键值存储体，键值存储体包含键向量矩阵 $W_{fc} = [k_1, k_2, \ldots, k_n]$ 及其偏置向量 $b_k$ 、激活函数 $\sigma$ 和值向量矩阵 $W_{proj} = [v_1, v_2, \ldots, v_n]$ 及其偏置向量 $b_v$ 。其中，每个键向量对应着输入文本中的特定模式，如 n-gram 或语义主题，而每个值向量则关联着模型输出的概率分布。

在查询存储体中找到相应知识的过程如下：对于某个输入的 Token，其查询向量为 $\mathbf{q}$ 。当 $\mathbf{q}$ 输入全连接前馈层时，首先与矩阵 $W_{fc}$ 相乘，计算出激活值向量 $\mathbf{a}$ ，其中每个分量代表 $\mathbf{q}$ 与对应键向量 $k$ 的关联程度。随后， $\mathbf{a}$ 与矩阵 $W_{proj}$ 相乘，得

到全连接前馈层的输出结果。该过程可以视为使用激活值对矩阵 $W_{proj}$ 中的所有值向量进行加权求和：

基于上述键值存储体的观点，全连接前馈层的隐藏层维度可被理解为其“记忆”的文本模式的数量，如果能够向全连接前馈层中添加更多与不同文本模式相关联的键值对，就可以向模型中插入新的事实信息，从而实现模型编辑。因此，T-Patcher在全连接前馈层中增加额外参数，即添加补丁。而且，T-Patcher仅在模型的最后一层添加补丁，以确保补丁能够充分修改模型的输出，而不被其他模型结构干扰。在下一节中，我们将详细介绍应该添加什么样的补丁。

5.3.2 补丁的形式

基于键值存储体的观点，T-Patcher将补丁的形式设计为键值对。具体地，T-Patcher在全连接前馈层中加入额外的键值对向量作为补丁，通过训练补丁参数从而实现模型编辑。补丁的形式如图5.11所示，它主要包括一个键向量 $\pmb{k}_p$ 、一个值向量 $\pmb{v}_p$ 和一个偏置项 $b_p$ 。

图5.11：补丁的形式。

在添加补丁后，全连接前馈层的输出被调整为：

其中， $a_{p}$ 为补丁的激活值，代表补丁对输入查询的响应程度。在添加补丁之后， $a_{p}$ 与值向量 $\mathbf{v}_{p}$ 之积会形成偏置项叠加到全连接前馈层的原始输出之上，以调整模型的输出。补丁就像是一个很小的修正器，只会被相关的输入查询激活。

5.3.3 补丁的实现

在确定了补丁的位置和形式之后，下一步便是训练补丁以实现模型编辑。本节将深入讨论如何训练这些补丁来有满足模型编辑的主要性质。T-Patcher冻结模型的原有参数，仅对新添加的补丁参数进行训练。此外，对于给定的编辑问题，T-Patcher为每个需要编辑的Token都添加一个补丁，从而可以精确地针对每个编辑需求进行调整。最后，T-Patcher从编辑的准确性和局部性两个角度出发对损失函数进行设计。接下来对其损失函数进行介绍。

1. 准确性

确保精确编辑是 T-Patcher 的核心目标之一。在训练过程中，为了强化补丁对模型的正确修改，首先需要针对准确性设计特定的损失函数。对于补丁的准确性，T-Patcher 主要关注两个方面：（1）确保补丁可以在目标输入下可以被激活；（2）一旦被激活，补丁应该能够准确地调整模型输出以符合预期的结果。为此，T-Patcher 设计了准确性损失 $L_{acc}$ ，它包括激活损失 $l_a$ 和编辑损失 $l_e$ ：

其中， $q_{e}$ 是编辑样本在全连接前馈层处的查询向量， $y_{e}$ 是该补丁对应的目标 Token， $p_{e}$ 是模型在补丁作用下的预测输出， $CE$ 是交叉熵损失函数， $\alpha$ 是激活损失 $l_{a}$ 的权重。

在准确性损失 $L_{Acc}$ 中，激活损失 $l_a$ 负责确保补丁在目标输入下可以被激活，它通过最大化编辑样本的查询向量 $\pmb{q}_e$ 对补丁的激活值，从而确保修补神经元对特定编辑需求的响应。另一方面，编辑损失 $l_e$ 主要确保补丁在被激活后能够有效地将模型输出调整为该补丁对应的目标 Token。具体而言，T-Patcher 使用交叉熵损失函数作为编辑损失，用于评估补丁调整后的输出 $p_e$ 与该补丁对应的目标 Token $y_e$ 之间的一致性，确保补丁的调整正确实现预期的修正效果。准确性损失是实现 T-Patcher 编辑目标的关键，它确保补丁在必要时被激活，并且激活后能够有效地达到预期的编辑效果。

2. 局部性

模型编辑不仅要确保精确的编辑，而且要求在对目标问题进行编辑时，不应影响模型在其他无关问题上的表现。为了保证编辑的局部性，T-Patcher设计了特定的损失函数来限制补丁的激活范围，确保其只在相关的输入上被激活。为了模拟无关数据的查询向量分布，以便在训练过程中控制激活范围，T-Patcher会随机保留一些先前已经处理过的查询向量，组成记忆数据集 $D_{M} = \{q_{i}\}_{i = 1}^{|D_{M}|}$ ，这些查询向量与当前的编辑目标无关。基于该数据集，T-Patcher定义了记忆损失 $L_{m}$ 来保证编辑的局部性，该损失包含 $l_{m1}$ 和 $l_{m2}$ 两项：

其中， $q_{i}$ 为无关问题的查询向量， $\beta$ 为指定的激活阈值， $\gamma$ 为指定的激活值差距的阈值。具体而言，第一项 $l_{m1}$ 负责确保补丁不会对无关的输入进行激活。这通过对每个无关输入的查询向量 $q_{i}$ 的激活值进行阈值限制实现，若激活值超过阈值 $\beta$ 则会产生惩罚。而第二项 $l_{m2}$ 旨在放大补丁对目标查询向量 $\mathbf{q}_{e}$ 和无关查询向量 $q_{i}$ 的激活值差距。这通过要求目标查询向量的激活值显著高于所有无关查询向量的激活值的最大值来实现。

将这些损失项整合，T-Patcher的总损失函数 $L_{p}$ 可以表达为：

其中， $\beta$ 是记忆损失项的权重。通过这种设计，T-Patcher不仅可以确保补丁正确地修改模型的输出，还能减少对其他问题的影响，从而实现准确且可靠的模型编辑。

尽管T-Patcher实现了模型的精确调整，在GPT-J模型上的准确性和泛化性较好，但是一些研究表明[27]，它也存在一些局限性。例如，在不同模型架构上，其性能会有所波动；在批量编辑时，对内存的需求较高，可能限制其在资源受限环境下的应用。相比之下，ROME方法表现得更加稳定。它将知识编辑视为一个带有线性等式约束的最小二乘问题，从而实现对模型特定知识的精确修改，在编辑的准确性、泛化性和局部性等方面都表现出色。该方法将在第5.4节介绍。