1.9 Q&A

Q: Can we set all the rewards as negative or positive?

A: In this chapter, we mentioned that a positive reward would encourage the agent to take an action and that a negative reward would discourage the agent from taking

the action. In fact, it is the relative reward values instead of the absolute values that determine encouragement or discouragement.

More specifically, we set $r_{\mathrm{boundary}} = -1$ , $r_{\mathrm{forbidden}} = -1$ , $r_{\mathrm{target}} = +1$ , and $r_{\mathrm{other}} = 0$ in this chapter. We can also add a common value to all these values without changing the resulting optimal policy. For example, we can add $-2$ to all the rewards to obtain $r_{\mathrm{boundary}} = -3$ , $r_{\mathrm{forbidden}} = -3$ , $r_{\mathrm{target}} = -1$ , and $r_{\mathrm{other}} = -2$ . Although the rewards are all negative, the resulting optimal policy is unchanged. That is because optimal policies are invariant to affine transformations of the rewards. Details will be given in Chapter 3.5.

Q: Is the reward a function of the next state?

A: We mentioned that the reward $r$ depends only on $s$ and $a$ but not the next state $s'$ . However, this may be counterintuitive since it is the next state that determines the reward in many cases. For example, the reward is positive when the next state is the target state. As a result, a question that naturally follows is whether a reward should depend on the next state. A mathematical rephrasing of this question is whether we should use $p(r|s,a,s')$ where $s'$ is the next state rather than $p(r|s,a)$ . The answer is that $r$ depends on $s$ , $a$ , and $s'$ . However, since $s'$ also depends on $s$ and $a$ , we can equivalently write $r$ as a function of $s$ and $a$ : $p(r|s,a) = \sum_{s'} p(r|s,a,s') p(s'|s,a)$ . In this way, the Bellman equation can be easily established as shown in Chapter 2.

Chapter 2

State Values and Bellman Equation

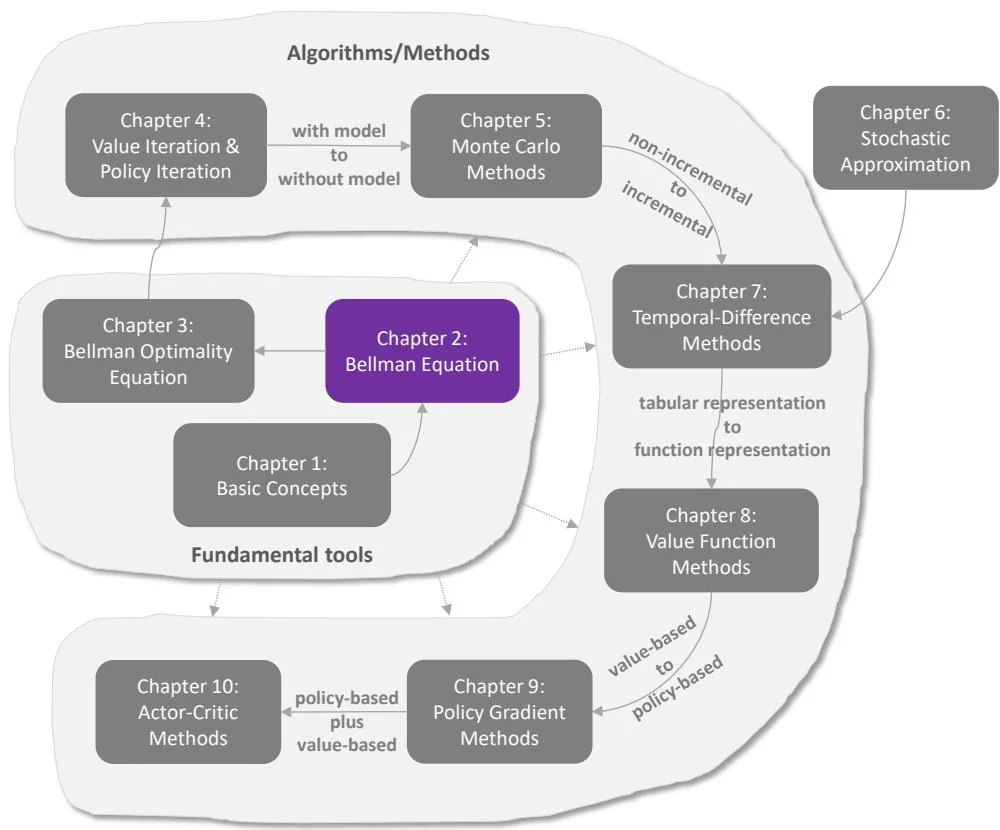
Figure 2.1: Where we are in this book.

This chapter introduces a core concept and an important tool. The core concept is the state value, which is defined as the average reward that an agent can obtain if it follows a given policy. The greater the state value is, the better the corresponding policy is. State values can be used as a metric to evaluate whether a policy is good or not. While state values are important, how can we analyze them? The answer is the Bellman equation, which is an important tool for analyzing state values. In a nutshell, the Bellman equation describes the relationships between the values of all states. By solving the Bellman equation, we can obtain the state values. This process is called policy evaluation, which is a fundamental concept in reinforcement learning. Finally, this

chapter introduces another important concept called the action value.