12.8 基于洗牌指令的线程束归约

SM 3.0中引入的“洗牌”（shuffle）指令，如8.6.1节中所述，可用于执行对一个线程束中32个线程的归约。通过使用洗牌指令的“蝴蝶”（butterfly）变形，最后5个步骤的对数步长的归约：

wsSum[tid] += wsSum[tid+16];  
wsSum[tid] += wsSum[tid+8];  
wsSum[tid] += wsSum[tid+4];  
wsSum[tid] += wsSum[tid+2];  
wsSum[tid] += wsSum[tid+1];

可改写为

int mySum = wsSum[tid];  
mySum += _shuf_xor(mySum, 16);  
mySum += _shuf_xor(mySum, 8);  
mySum += _shuf_xor(mySum, 4);  
mySum += _shuf_xor(mySum, 2);  
mySum += _shuf_xor(mySum, 1);

然后，线程束中的所有线程把得到的归约值保存于mySum。图12-2演示了这一线程束扫描原语操作。每个线程的和显示为 $4\mathrm{W} \times 8\mathrm{H}$ 矩形，用深色方形指示哪些线程对每个线程的部分和做出了贡献。（除去插图，最上面一行显示了对应于每个线程的贡献的方形。）对数步长归约每前进一步，贡献的数量加倍，直到每个线程都拥有一个完整的归约值。[1]

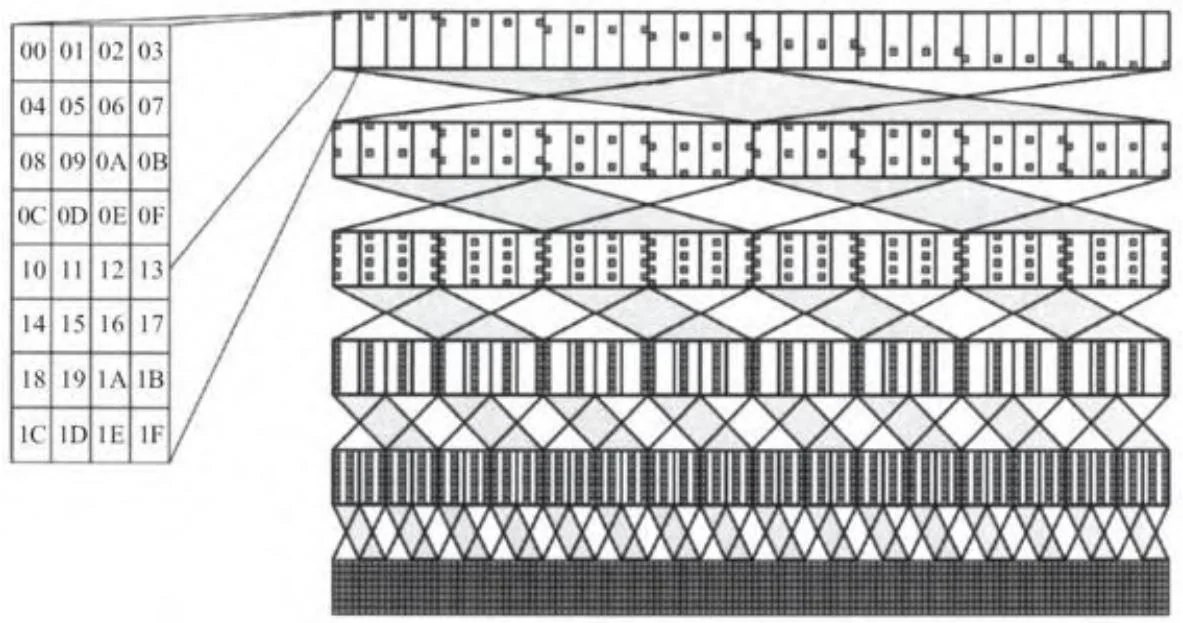
图12-2 使用洗牌指令的归约

[1] 向上洗牌（shuffle-up）或向下洗牌（shuffle-down）的变体可被用来实现归约，但它们需要的次数与蝴蝶（XOR）变体一样，并且最终的归约值仅保存在一个线程中。