12.8 Warp Reduction with Shuffle

SM 3.0 introduced the "shuffle" instruction, described in Section 8.6.1, that can be used to perform a reduction across the 32 threads in a warp. By using the "butterfly" variant of the shuffle instruction, the final 5 steps of the log-step reduction

wsSum [tid] += wsSum [tid + 16];

wsSum [tid] += wsSum [tid + 8];

wsSum [tid] += wsSum [tid + 4];

wsSum [tid] += wsSum [tid + 2];

wsSum [tid] += wsSum [tid + 1];

can be rewritten as

int mySum = wsSum[tid];

mySum $+ =$ shuf_xor (mySum, 16);

mySum $+ =$ shuf_xor(mySum,8）;

mySum $+ =$ shuf_xor（mySum，4）;

mySum $+ =$ shuf_xor (mySum, 2);

mySum $+ =$ shuf_xor ( mySum, 1 );

All threads in the warp then contain the reduction in mySum. Figure 12.2 illustrates the operation of this warp scan primitive. Each thread's sum is shown as a $4W \times 8H$ rectangle, with a dark square showing which threads have contributed to each thread's partial sum. (Besides the inset, the top row shows which squares correspond to each thread's contribution.) With each step in the log-step reduction, the number of contributions doubles until every thread has a full reduction.5

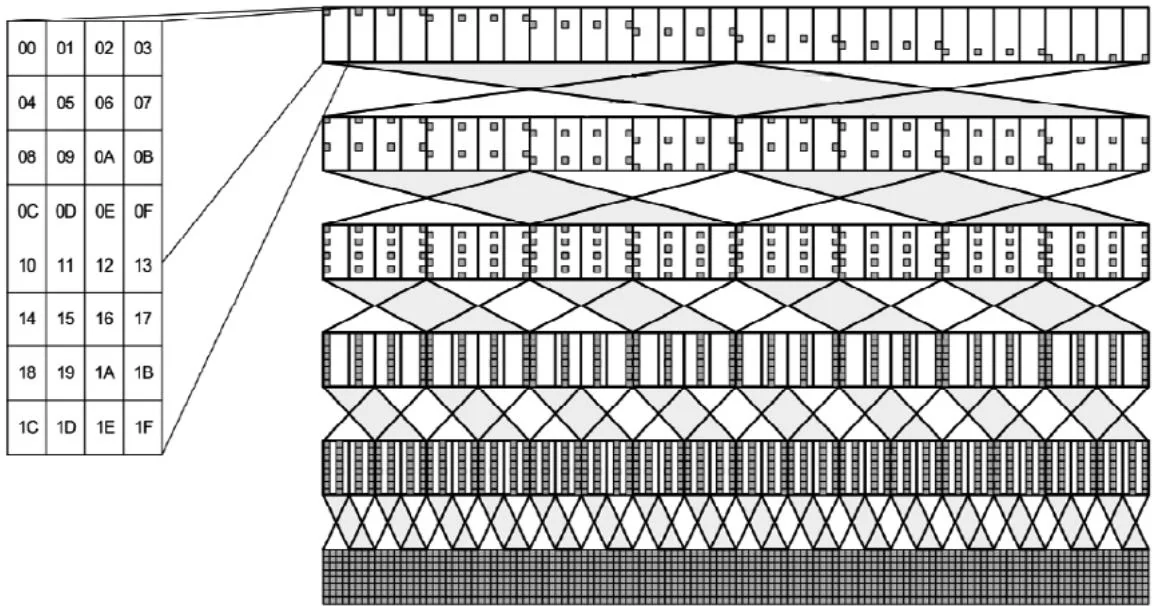
Figure 12.2 Reduction using shuffle instruction.

This page intentionally left blank

Scan

Scan, also known as prefix scan, prefix sum, or parallel prefix sum, is an important primitive in parallel programming and is used as a building block for many different algorithms, including but not limited to the following.

Radix sort

• Quicksort
  Stream compaction and stream splitting

• Sparse matrix-vector multiplication

• Minimum spanning tree construction

• Computation of summed area tables

This chapter starts with a description of the algorithm and a few variations, discusses an early implementation strategy and how Scan algorithms can be described in terms of circuit diagrams, and then provides detailed descriptions of Scan implementations for CUDA. The References section covers both the Scan algorithm and the parallel prefix sum circuit problem in hardware design.