13._卡方分布χ²-前世今生-Part4 - Probability Theory and Mathematical Statistics

卡方分布χ²-前世今生

χ的写法很像英文字母X，又像生物课本中的人的染色体符号，所以一开始我对这个希腊字母感觉非常陌生。

卡方分布是概率论与统计学中常用的一种概率分布。这个分布有些特别，因为它在不同的应用场景有不同的自由度。而且他也不用来建模的，在前面介绍过很多分布，比如二项分布，指数分布等，当在实际生活中遇到问题时，会尽可能把生活模型往这些分布模型上靠，但是卡方分布不是，他主要用来检验的，就是用来检验你网上靠的模型是不是准确。

如果做一个比喻，大家都去淘金，但是淘金要过一条河，前面介绍的各种分布（指数分布、正态分布、二项分布等）就是各种淘金者，而卡方分布就像一个摆渡者，他本身不去淘金，但是你要淘金，可以坐他的小船，他会渡你过岸。

卡方所以在不同的场景下使用不同的自由计算公式。如果是用χ²检验列联表的时候，自由度为：（行数-1）×（列数-1）；而如果用χ²检验进行拟合优度检验，那么自由度则为：k-1。

另外，卡方分布与正态分布变量相关，也就是说卡方分布其实源自于正态分布。

我们查了下互联网资料，特别是维基百科中的资料索引，一直查下去，发现有很多人都支持是德国的大地测量学家F.R.Helmert在1875 年关于正态总体样本方差分布的研究中，是他首次描述了这种分布。

因此在德语中这个分布被称为Helmert'sche或“Helmert 分布”，中文翻译为 赫尔默特分布。

后来，英国数学家卡尔·皮尔逊 (Karl Pearson,以下简称Pearson）又独立地在1900年在Philosophical杂志的一篇论文中正式提出这个概念，并且他还和助手一起计算出了卡方值检验表，使得卡方分布得以实用化。

那为啥Pearson为啥会引用希腊字母和阿拉伯数字的组合——χ²作为这个概率分布的名字呢？

主要是1895年Pearson在伦敦大学学院时，他在《对数学进化论的贡献》(Contributions to the Mathematical Theory of Evolution)论文集中发表过一篇关于回归、遗传及Panimixia（混合物？）的论文，他在论文中将多元正态密度函数中的指数部分写成 -½·χ²，这个习惯Pearson一直沿用到了刚才说到的1900年的那篇文章。如下图的考古

$图片$

考古如下 $图片$

在论文中Pearson 多处的推导用了正态分布的σ符号来表示标准差，这也就间接表示了卡方分布源自正态分布。

最后，又是R. A. Fisher 在1924年把卡方分布纳入了正态分布族。

从Pearson的案例切入对χ²理解

Pearson最早发表卡方分布的论文里，列举了日后在教科书里面经常见到的应用案例：样本的抽样比例分布，和理论的概率分布之间是否有显著差异。

就是文章开头里，统计量服从卡方分布的例子，我们在前面Part1和 Part2 里已经介绍过这个公式

\chi^2=\sum_{i=1}^k \frac{\left(O_i-E_i\right)^2}{E_i}

只不过他的第一个例子，是和Weldon教授一起搞的掷骰子场景。

这个例子比较长，我也打算从中慢慢的提取出卡方分布推导的切入点，而且可能切入点还不止一个。

频率已知，或假设先验已知：12个骰子的实验和轮盘实验

Pearson 和Weldon教授一起做了个实验：有12个骰子，连续扔26306次，Weldon教授提供了出现5点或6点的骰子数量的理论频数，以及他的学生们观测到的实际频数。

Pearson的论文并没有给出理论频数m的计算方法，而是直接给出了结果，所以第一次看的时候比较晦涩，我只好自己尝试补充了一下，如下表：

$图片$

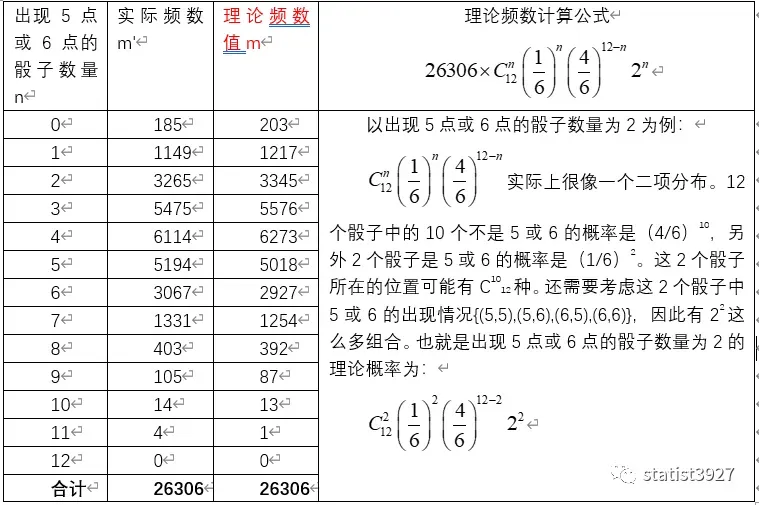
比较一下上表中的理论频数值m的分布，和实际频数值m’的分布还是有些差异的，特别的，出现5次，6次实际的频数要比理论频数高一些（m’-m 分别为176和140）。

这种偏差是否就否定了投骰子的实验结果和理论的概率分布不一致？或者说m’不服从m分布？

此时可以通过计算卡方值进行测算，如下表：

$图片$

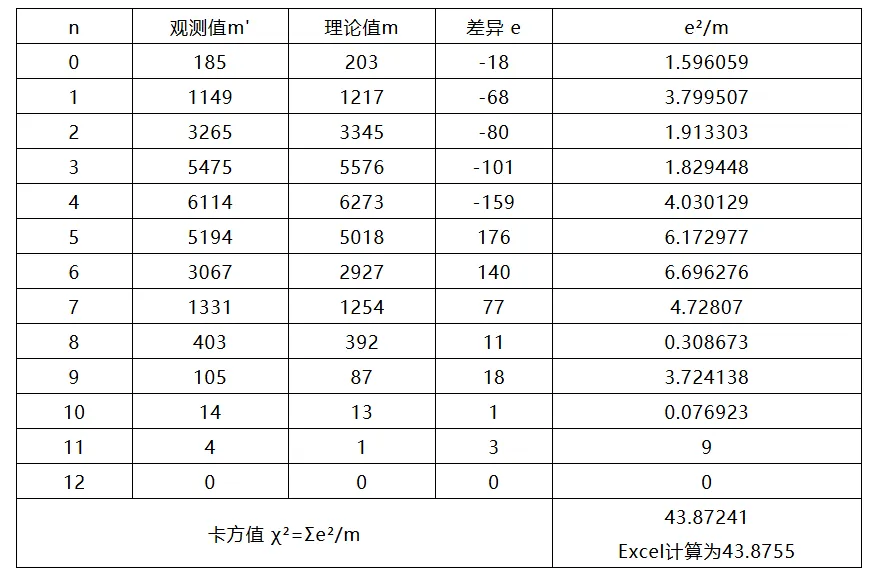
有13组数据，要代入一个P值的概率计算公式：

P=e^{-\frac{1}{2} \chi^2}\left(1+\frac{\chi^2}{2}+\frac{\chi^4}{2 \cdot 4}+\frac{\chi^6}{2 \cdot 4 \cdot 6}+\frac{\chi^8}{2 \cdot 4 \cdot 6 \cdot 8}+\frac{\chi^{10}}{2 \cdot 4 \cdot 6 \cdot 8 \cdot 10}\right) ...(1.1)

经过计算得到P=0.000016

这下第一个问题冒出来了，式1.1 是怎么来的？后面会说

从这P值如此之小，其实可以直接做出结论，观测值的频数分布和理论频数分布在统计上的差异是不显著的。

还有一个直观的感受它们之间差异不显著的指标是期望值对比。

如果把上面实验结果的理论期望，也就是 Σ（理论频率×出现5或6点骰子的个数），和观测值的期望做一个对比，会发现差异也是非常的小。

理论期望经过计算=4，也就是

\begin{aligned} E(n) & =\sum_{n=0}^{12} n \cdot C_{12}^n\left(\frac{1}{6}\right)^n\left(\frac{4}{6}\right)^{12-n} 2^n \\ & =4 \end{aligned}

而每一个观测的m’的频率，可以用m’/26306计算得到。

那么观测期望值经过计算=4.05238 （后面还有一堆小数）

\begin{aligned} E(n)^{\prime} & =\sum_{n=0}^{12} n \cdot \frac{m_n^{\prime}}{26306} \\ & =4.05238 \end{aligned}

直观的看着2个期望值已经差异很小了。 2个期望之间的差异如此之小，Pearson 认为可能就是理想中的骰子和实际中骰子有差异造成的。

1.1 公式是如何得来的

在实际应用中，搞清楚为什么要通过它来计算P值，是理解卡方分布的一个关键。

因为早期计算机还没普及之前，人们通过“查表”来估算P值，查的就是用这个式子计算出来的结果。

$图片$

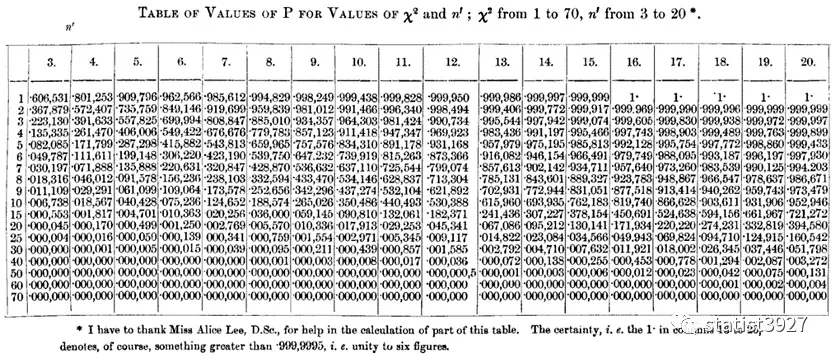
下面介绍 Pearson 是怎么推出卡方分布的。

1. χ2的定义，从标准正态分布的一般情况入手。

首先，令x1，x2，…xn为n维的误差系统，每一维变量的标准差为σ1，σ2…σn，误差变量之间的相关系数分别为r12，r13，r23，…rn-1,n。

并由下式构建成一个频率曲面：

$图片$

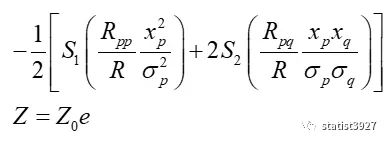
在上面的式子中，R是相关系数行列式

$图片$

Rpp是主对角线元素的余子式，

Rpq是非主对角线元素的余子式。

S1是求和SUM的意思, 它代表p为脚标的每个值的和；

S2是p和q为脚标的每对值的和（p≠q）。

S1和S2的表述，转换成我们现在熟悉的运算符号Σ，就是 $图片$

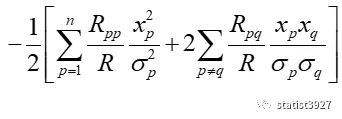
基于上面的信息，令 $图片$

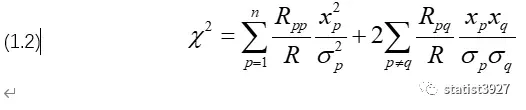
在这里，χ2被最初地定义出来。

χ2被定义出来后，目的是要为后续的数值计算服务的。

但（1.2）式的计算量太大，尤其是一堆的行列式要算。因此必须将（1.2）式进行简化，不然在没有计算机的年代，数值计算会是一个噩梦。

（简化过程会在下一篇文章介绍）

对（1.2）进行观察，Pearson虽然没有显性化地介绍χ2被是服从标准正态分布的，但还是有个细节能看出来

这个细节就是 “误差”两个字，把误差（Error）代入（1.2），就发现它本质就是标准正态分布的Z值变换过程：

$图片$

而标准正态分布的Z值变换，正是

$图片$

这也是为什么很多B站UP主在介绍卡方分布时，会强调“卡方分布来自于标准正态分布”。

Pearson称χ2的（1.2）表达式可以看成是一个“广义椭球”。

且χ≥0，可覆盖[0, +∞]的空间。

χ2是如何定义的搞明白了，那它P值的关系，又怎么说呢？

当这个“椭球”开始挤压最终变成了一个球体的时候，X1，X2，X3……Xn则成为了这个球体的坐标。

这个误差系统观测到的频率（样本的）和整个误差系统频率（理论上的），它们之间的比率，也就是P值的最初含义。

可能看文字看得有些晕乎，那么看式子吧。

P由下式给出：

$图片$

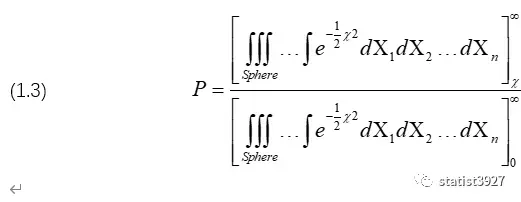
式中，分子是从χ→∞的n重积分，分母是0→∞的n重积分。

分子分母中正态分布的常数项2π-n/2，都被约掉了。

将这个n维球坐标系进行极坐标变换，由χ来表示极坐标系中的那个径向坐标r，那么整个式子就可以简化成如下：

$图片$

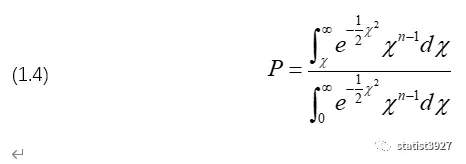
（1.3）→（1.4）的过程，Pearson没有展示出来，我在此补充一下

我去查了资料，（1.3）→（1.4）的过程，Pearson应该用的是超球坐标系下Jacobian（雅可比行列式）进行变换的。

设X1，X2，……Xn为笛卡尔坐标系下的n维球坐标

$图片$

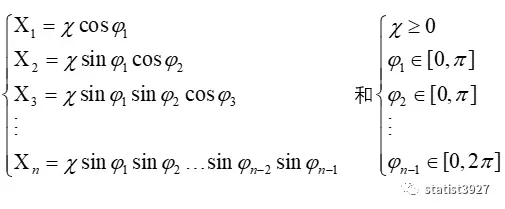
由Jacobian行列式 $图片$

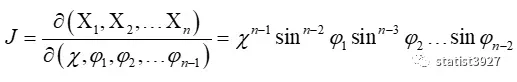
对体积元素（Volume element，dV）dX1dX2……dXn进行变换，得到 $图片$

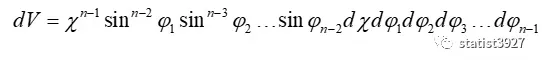
将变换结果代入（1.3）式分子的体积元素，得

$图片$

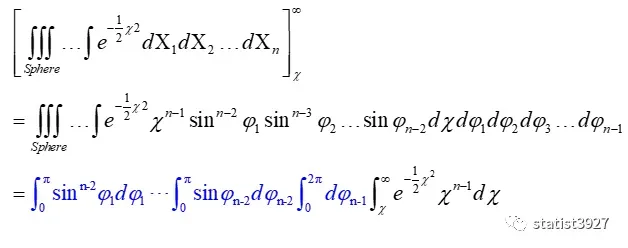
将变换结果代入（1.3）式的分母的体积元素，同理可得

$图片$

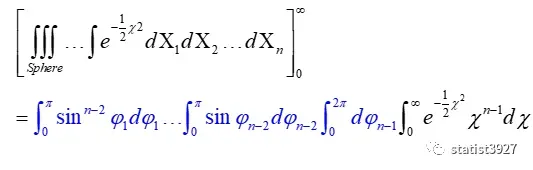
分子分母中的蓝色部分，是可以约掉的。

所以（1.3）式才会简化得到（1.4）式。

基于前面的设定，χ≥0，P的范围就在 0≤P≤1。

但是，带着积分符号还是不方便计算，于是还要对（1.4）进行变型或简化。

3、P值计算的进一步简化（可有限代数运算）

简化的目标：消除（1.4）式中的积分符号，或者最大限度的少用积分运算。

这里不得不佩服Pearson的分部积分法运算技巧。

Pearson没有把推导的关键步骤给显性化，只是将很长的推导过程写成了2步，并提示是采用“分部积分法”做出来的。我在此补充完整的过程，因为这个分部积分法用了不止一次。

设原函数为：vu

构建分部积分的式子，为

$图片$

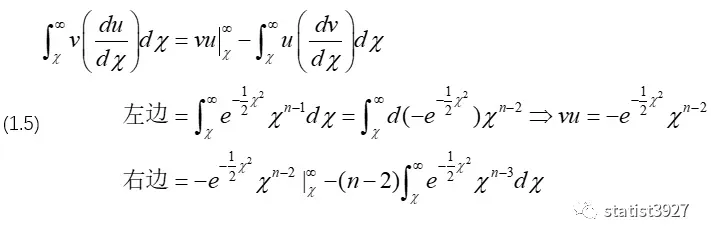
先研究（1.5）“右边”一个牛顿-莱布尼茨公式可以解决的部分

$图片$

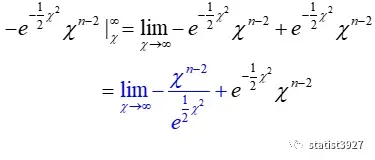
使用n-2次洛必达法则，上式的蓝色部分可以得到

$图片$

由此，（1.5）中“左边“和“右边”整理后，可以写成

$图片$

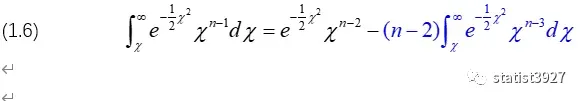
（1.6）中蓝色部分是可以按照上面的方法继续递推下去的，我在此仅展示递推一次：

$图片$

上式的最后一行，提取公因式(n-2)(n-4)(n-6)……(n-2r)，最终得到

$图片$

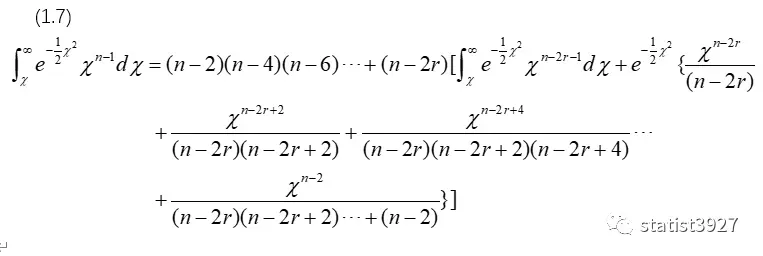
以上（1.7）就是（1.4）中分子的变形。

但说实话，算到这一步，我当时一点儿也不觉得这个叫“简化”，式子还越算越多了！

那接下来我们把（1.4）中P等式的分母简化试试？

这个过程要容易些，因为积分符号的上下限是确定的0和∞，因此代入后会得到分母的变型：

$图片$

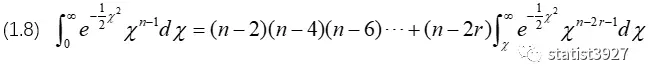
分子分母的变型都计算得到了，那直接（1.7）/(1.8)算一算？

别急，要分2种场景讨论分子和分母相除：

I: 当n是奇数的时候（提前告知，此时的n是考虑了自由度，下同）:

（1.7）和 (1.8) 元素的个数大约是n的一半，于是令r=(n-1)/2，

将r代入（1.7）/(1.8)，得到

$图片$

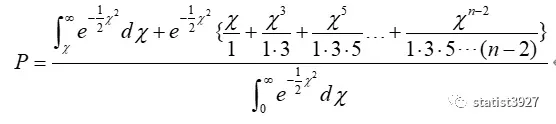
咦？这时候分母还是带积分符号啊？

说好的减少积分符号呢？

我在《为什么正态分布中有个π》的文章中，介绍了e-x2的积分是π1/2，因此知道了分母的这个特点后，上式可以直接变形为

$图片$

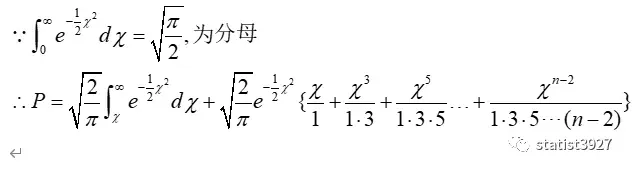
于是当n为奇数时，P的计算方法为如下：

$图片$

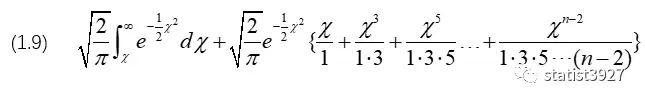
当n为偶数时，

令r=½n-1，将r代入（1.7）/(1.8)，得到

$图片$

由此，得到n为偶数时，P的结果为

$图片$

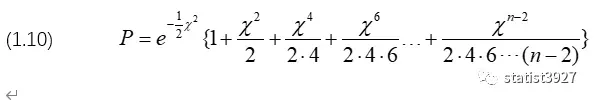
此时（1.10）就是回答了文章第一部分中，式子（1.1）是怎么来的。

我觉得这个公式的编号，一个是1.1，一个是1.10，刚好完成一个闭环啊。

插入花絮：

在上面的过程中我也发现了Pearson论文里的一个小小问题：

他的推导过程有一步，被出版社漏印了积分元素dχ

如果能回到123年前的伦敦，我告知Pearson他这个小纰漏，他会不会很高兴地请我喝下午茶呢，呵呵：）

$图片$

（花絮完）

之前的推导，其实还有一个小尾巴问题的：

回顾之前的那个（1.1）式子

$图片$

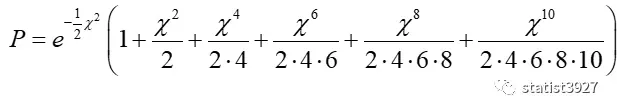
它就是在上一篇文章中的首个例子：掷12个骰子，点数为5或6的骰子个数，共有13种场景。

为什么Pearson只计算n到了12？

或者他不选择当n为13时的计算式（1.9）？

这里涉及到了自由度的问题。

论文里Pearson简单介绍了下为什么要考虑自由度，他指出，

假设有n+1个分组，有n+1个误差观测频数 m1’,m2’……mn+1’，同时也存在n+1个理论频数m1, m2……mn+1，因此就会有n+1个观测误差和理论误差的差异，e1,e2,……en+1。

如果e1+e2+……+en+1=0，那么只要其中n个e确定，那么第n+1个e值就确定了。

所以在这种理论状态下，自由度就是n。

13组观测值，最后计算时要考虑自由度为12。

后来，我也继续查阅了一些后人关于卡方检验自由度的资料，补充一下：把掷骰子的实验场景看成是拟合优度的检验，这种场景下，它的自由度为13-1，也就是12。

到此，总算是搞明白χ2值和P之间的关系原来还分两种场景的！

接下来，我们继续简化计算（1.2）中χ2值

本文摘自微信公众号：深入理解卡方分布（上）

深入理解卡方分布（中）