15._t分布

假设车间生产了一批螺丝，你想检验这些产品质量情况，你随机抽查了一些螺丝，此时就可以使用统计抽样的四大分布是：正态分布、卡方分布、t分布和F分布，他们分别对应 Z检验、卡方检验、t检验和F检验。如果你抽查的样本比较多(n>30)优先使用Z检验(对应正态分布)，如果抽查样本比较少(n<20)则使用t检验(对应t分布)，如果你想比较两个机床生产的螺丝质量差异则使用F检验(对应F分布)。如果想分析螺丝质量和原材料质量的关系则使用χ²卡方检验(对应卡方分布)

χ²分布、t分布、F分布的主要用途，其实不是拿来用于自然现象的建模，而是用于假设检验用的。只有正态分布既可以进行建模又可以进行检验

①：某地某年高考后随机抽得 15 名男生， 12 名女生的数学考试成绩如下：

男生： 49 48 47 53 51 43 39 57 56 46 42 44 55 44 40

女生： 46 40 47 51 43 36 43 38 48 54 48 34

这 27 名学生的成绩能说明这个地区男女生的数学考试成绩不相上下吗（显著性水平 $\alpha=0.05$ ）？

②：某厂铸造车间为提高缸体的耐磨性而试制了一种镍合金铸件以取代一种铜合金铸件，现从两种铸件中各抽一个样本进行硬度测试，其结果如下。

镍合金铸件 $(X): 72.0,69.5,74.0,70.5,71.8$ . 铜合金铸件 $(Y): 69.8,70.0,72.0,68.5,73.0,70.0$ 。根据以往经验知, 硬度 $X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right)$ , 且 $\sigma_1=\sigma_2=2$ , 试在显著性水平 $\alpha=0.05$ 下, 比较镍合金铸件硬度有无显著提高.

关于他们的解答请参考T检验

理解t分布

首先需要明白，不管是上一节介绍的卡方分布还是本节介绍的t分布，他们主要用于抽样检验的，他不是对数据进行建模。而是用于对数据模型进行进行检验，什么意思？

考虑如下一个情况: 你在白纸上写了一个“赢”字，然后让AI识别：此时AI可以使用两种数据模型：

模型1：采用正态模型。 AI判断这个字是“赢”字的可能性为90%，是“羸”字的可能性为80%

模型2：采用t模型。这个字是“赢”字的可能性为90%，是“羸”字的可能性为80%

可以看到，使用不同的模型，AI都“比较能”识别字的对错，这是横向对比，如果切换到竖向对边呢？即到底是正态模型更准确还是t模型更准确？此时就是大模型对比，而不是字的对比。

我们说，不管是正态模型还是t模型，他们本身没有对与错，只有好或者不好。下面的t分布的引入会进一步介绍这个意思。

t分布

定义

设随机变量 $X \sim N(0,1), Y \sim {\chi}^2(n)$ ，且 $X$ 与 $Y$ 相互独立, 则称

\boxed{ T = \dfrac{X}{\sqrt{Y / n}} }

所服从的分布为自由度为 $n$ 的 $t$ 分布，记为 $T \sim t(n)$ .

$t$ -分布的密度函数

f(x)=\dfrac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n \pi } \Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^2}{n}\right)^{-\frac{n+1}{2}},-\infty<x \wedge+\infty

性质: (1) $f(-x)=f(x)$ (2) $f^{\prime}(x)=-(n+3) x f(x) \quad \therefore f(x) \uparrow(x<0), f(x) \downarrow(x>0)$ (3) $\lim _{n \rightarrow+\infty} f(x)=\lim _{n \rightarrow+\infty} \frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n \pi} \Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^2}{n}\right)^{-\frac{n+1}{2}}=\frac{1}{\sqrt{2 \pi}} e ^{-\frac{x^2}{2}}$

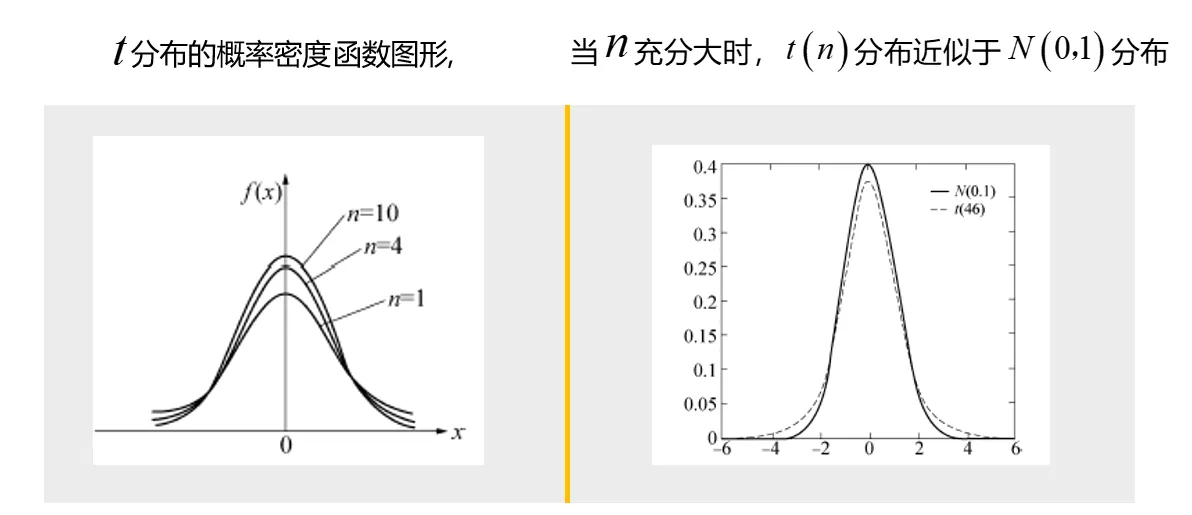
密度函数如下 {width=500px}

还是那句话，t分布的概率密度函数是不可能记住的，也不需要记住。但我们还是得分析一下定义。t分布是偶函数，关于y轴对称。可以看出，t变量是一个正态变量除以卡方变量比上自由度的开方得到的。分子是正态变量，分母源于正态变量，所以，t变量也源于正态变量。明白t变量的构造形式，后面你对各种各样的涉及t统计量的参数估计、假设检验，就不至于很懵了。反正所有的t统计量的样子都是一个正态变量除以卡方变量（实在不行，理解成方差也能应对大多数场景）比上n的开方。

可以证明当 $n>45$ 时，他可以看成正态分布。

分位数

设 $X \sim t(n)$ ，记它的 $\alpha$ 分位数为 $t_\alpha(n)$ ，即 $t_\alpha(n)$ 满足

P\left(X \leq t_\alpha(n)\right)=\alpha .

根据 $t$ 分布密度函数的对称性，有性质 $t_\alpha(n)=-t_{1-\alpha}(n)$ . 该性质类似于正态分布的分位数性质. 分位数值查表可得. 比如 $t_{0.95}(10)=-t_{0.05}(10)=1.812$ .

数学期望与方差

$t$ -分布 $t(n)$ 数学期望: $\mu=0$ ，方差: $\sigma^2=n /(n-2)(n>2)$

t分布的引入

$t$ 分布是统计学中的一类重要分布, 它与标准正态分布的微小差别是由英国统计学家戈塞特（Gosset）发现的。在 1908 年以前，统计学的主要用武之地先是社会统计，尤其是人口统计, 后来加入生物统计问题。这些问题的特点是, 数据一般都是大量的、自然采集的，所用的方法多以中心极限定理为依据，总是归结到正态，K．皮尔逊就是此时统计界的权威，他认为正态分布是上帝赐给人们唯一正确的分布。但到了 20 世纪，受人工控制的试验条件下所得数据的统计分析问题日渐引人注意。此时的数据量一般不大，故那种仅依赖于中心极限定理的传统方法开始受到质疑。这个方向的先驱就是戈塞特和费希尔.

戈塞特年轻时在牛津大学学习数学和化学, 1899 年开始在一家酿酒厂担任酿酒化学技师, 从事试验和数据分析工作. 由于戈塞特接触的样本容量都较小, 只有四五个,通过大量试验数据的积累，戈塞特发现 $t=\sqrt{n}(\bar{x}-\mu) / s$ 的分布与传统认为的 $N(0,1)$ 分布并不同, 特别是尾部概率相差较大。由此, 戈塞特怀疑是否有另一个分布族存在, 但他的统计学功底不足以解决他发现的问题, 于是, 戈塞特于1906年到1907年到 K. 皮尔逊那里学习统计学, 并着重研究少量数据的统计分析问题，1908年他在 Biometrics 杂志上以笔名 Student（工厂不允许其发表论文）发表了使他名垂统计史册的论文：均值的或然误差。在这篇文章中，他提出了如下结果: 设 $x_1, x_2, \cdots, x_n$ 是来自 $N\left(\mu, \sigma^2\right)$ 的独立同分布样本, $\mu, \sigma^2$ 均未知, 则 $\frac{\sqrt{n}(\bar{x}-\mu)}{s}$ 服从自由度为 $n-1$ 的 $t$ 分布. 可以说, $t$ 分布的发现在统计学史上具有划时代的意义，打破了正态分布一统天下的局面，开创了小样本统计推断的新纪元，小样本统计分析由此引起了广大统计科研工作者的重视。事实上，戈塞特的证明存在着漏洞，费希尔注意到这个问题并于 1922 年给出了此问题的完整证明, 并编制了 $t$ 分布的分位数表.

$图片$

Student，则是戈塞特的笔名。他当年在爱尔兰都柏林的一家酒厂工作，因为行业机密，酒厂不允许他的工作内容外泄，所以当他署了student的笔名，因此后来人知道student，知道t，却不知道是Gosset

这就是t分布又称为学生Student 分布的由来。

看懂 $t$ 分布和正态分布的区别

因为正态分布太常见了，以至于我们当拿到一组数据时，第一时间想到的是：这批数据服从正态分布，然后从正态分布的特点进行数据建模，对数据进行估算，但是 $t$ 分布告诉我们，在小样本的情况下，这种想法并不一定正确。

在研究一个分布的时候，我们很多时候可能会对极大值特别的敏感。比如说，我是一个小型公司的老板，收到了一份这样的风险分析， 0.1 的概率赔 10 万， 0.05 的概率赔 20 万，等等。这些数字我大概都是一扫而过，因为这些钱我完全赔的起。但假如说我看到了一个 0.01 的概率赔 1000 万，我估计眼睛就瞪圆了。虽然说 0.01 不算是一个大的概率，但是赔这么多钱我们公司可能就破产了。

因此，理解 $t$ 分布和正态分布最核心的区别是：那些细微的区别。

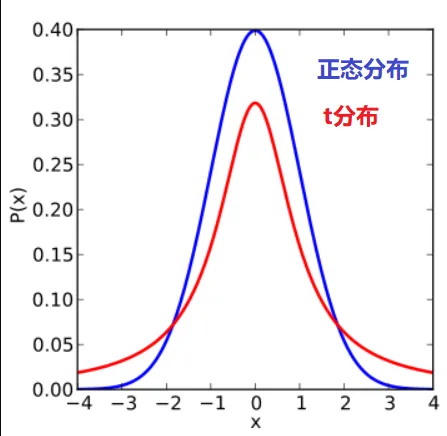
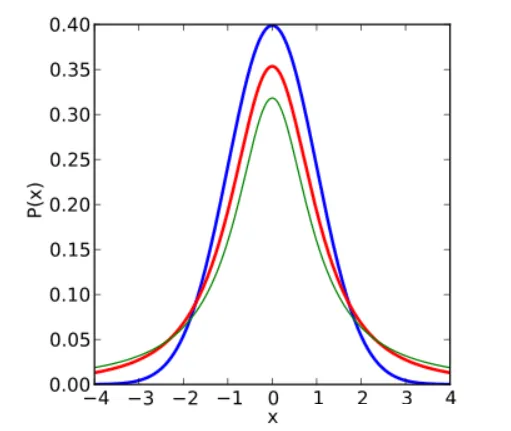
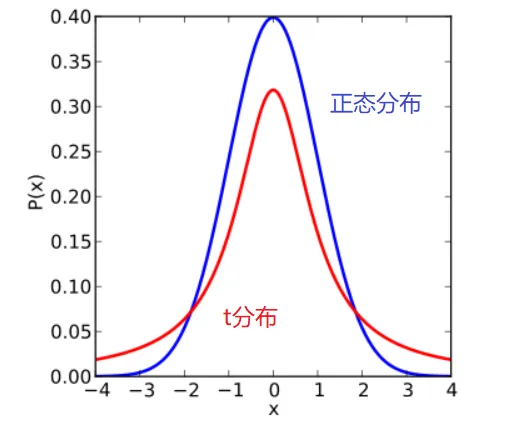
下图红色是t分布，蓝色是正态分布，自由度为1 $图片$

自由度为2 $图片$

自由度为10 $图片$

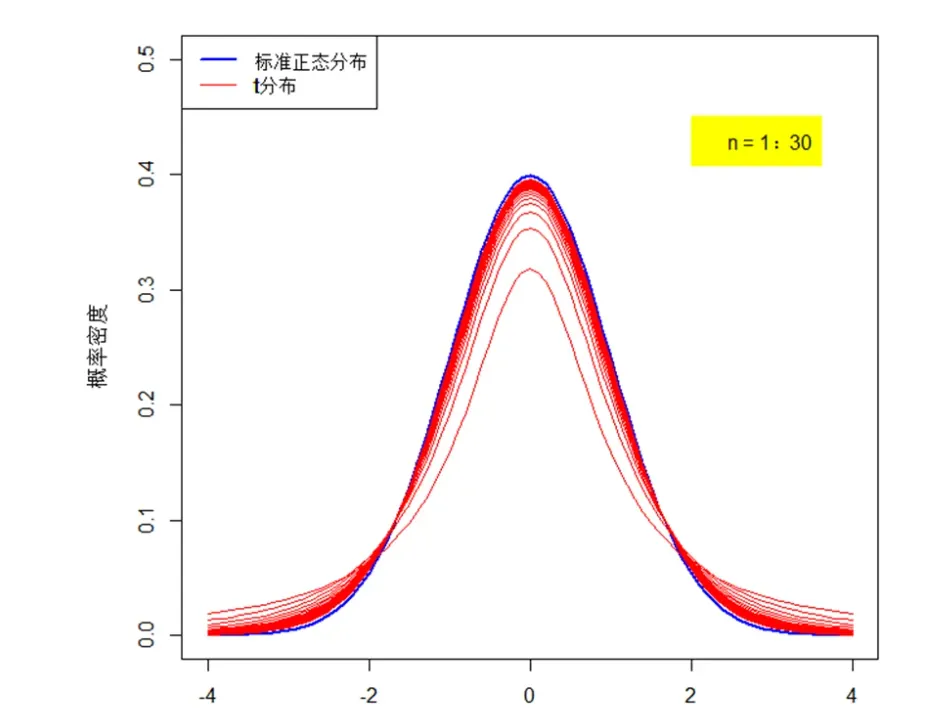
可见，随着样本量n / 自由度的增加，t分布越来越接近正态分布。正态分布，可以看做只是t分布的一个特例而已。

大家仔细比较一下下图。t分布（红色）虽然也是钟型曲线，但是中间较低、两侧尾巴却很高。这就是t分布的优势！这个特征相当重要，百年来，t分布就指着这个特征活着的！

尾部的高度，有十分重要的统计学意义

正态分布的曲线不具备“宽厚”的特征。它的尾部很低，尾部与横轴之间高度很“狭窄”。也就是说，正态分布不能够容忍它长长的尾部出现大概率的事件，所以正态分布就很无奈地，将这一点纳入它的胸膛而非留在尾部。于是乎，恶果就出现了：图中正态分布的均数，远远偏离了大多数点所在的位置，标准差也极大。总之，与我们所期待的很不一致。结合上面的简单引例，老板收到风险报告，当使用正态分布进行建模时，1000万的赔偿是不可能发生的，但是使用t分布进行数学建模时，这个事件仍可能发生。这是细微的区别，可见使用不同的分布进行数学建模，得出的结论，会对企业领导层的决策致关重要。 $图片$

在那种情况下你使用t分布？

假设您抽查了一批物件，得到一组数据，现在你将用一个函数来拟合遮住数据，这个拟合函数就是抽样的核心。

总体服从正态分布，但方差 $\left(\sigma^2\right)$ 未知
小样本 $(n<30)$

前提：在有了标准正态分布 $(X)$ 和卡方分布 $(Y)$ 的前提下， 2.做法: 用标准正态分布跟卡方分布的随机变量比。
数据处理: 卡方分布需要把自由度给除掉：如果不除，卡方分布加的随机变量越来越多，分母就会趋近于无穷。除掉自由度类似于一种归一化。

还得开根号：进行单位的统一，这样两个数字一比，就把单位给消了，变成了无量纲的数字。这样子得到的分布就和标准正态分布差不多。如果是两个随机变量相除，一般跟坋布或者F分布有关。 t分布要求分子的随机变量是正态分布，如果遇到一个正态随机变量，除以一个卡方随机变量开根号的那种就跟分布有关。

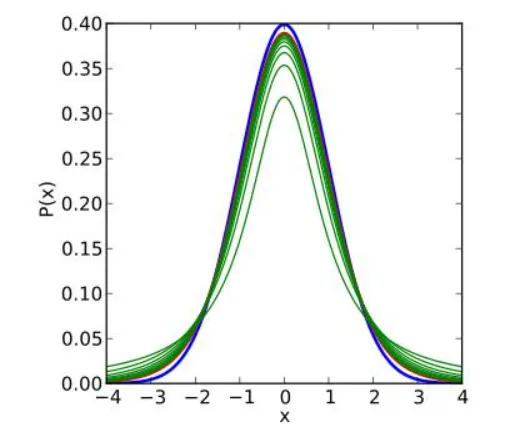
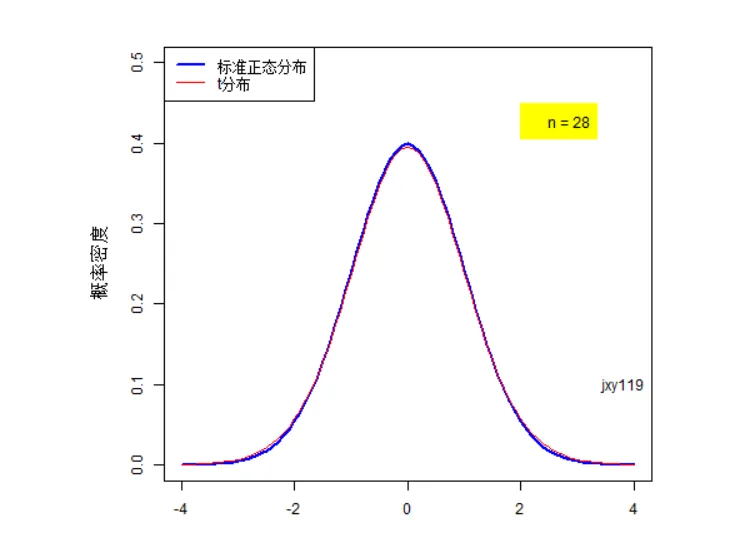
不同自由度下的t分布和正态分布比较 $图片$ {WIDTH=400PX}

$图片$ {WIDTH=400PX}

我们可以看到t分布的一些性质。第一，t 分布是类似正态分布的一种对称分布，它通常要比正态分布平坦和分散。我们经常说，小样本时，t检验的效果更好，就是由这条性质决定的。因为尾部厚啊，能够包含更多的极端情况啊。第二，它只依赖一个特定的分布依赖于称之为自由度的参数。随着自由度的增大，分布也逐渐趋于正态分布。你可能注意到了，当样本数量n大于30，t分布几乎与正态分布重合了。这也是统计学里面把30作为大样本和小样本分界线的一个原因。（怎么样？解开了你心中多年的谜团吧）。这个性质也直接给了很多软件偷懒的机会。不知道你注意到没有，你做回归分析之类的稍微复杂一点的数据分析，都会遇到对参数的检验。正常情况下，我们要遵守“大样本用正态检验，小样本用t检验”的原则。但是实际操作上，小样本时候t检验效果好，大样本时，t检验又跟正态检验差不多。那做软件的时候，干脆直接都用t检验好啦。谁知道用户的数据到底大样本还是小样本。所以，你可以看到，像R啊，Eview啊，这些软件干脆都直接给出t值和t检验结果。

例题

例 设 $T \sim t(10)$ ，求常数 $C$ 使 $P(T>c)=0.95$ ；解由 $P(T>c)=0.95$ 可知， $P(T \leq c)=0.05$ ，所以 $C=t_{0.05}(10)$ ，由 t 分布的密度函数图像对称性，所以 $c=t_{0.05}(10)=-t_{0.95}(10)$ ，查附录 6 得 $c=-1.8125$ .

例 设 $X_1, X_2, \cdots, X_5$ 为取自标准正态总体的一个样本，

试给出常数 $d$ ，使得

d \frac{X_1+X_2}{\sqrt{X_3^2+X_4^2+X_5^2}}

服从 $t$ 分布，并指出它的自由度.

解：因 $X_i \sim N(0,1), i=1,2, \cdots, 5$ ，且相互独立，故有

X_3^2+X_4^2+X_5^2 \sim \chi^2(3), X_1+X_2 \sim N(0,2)

且两者相互独立，由定义知

\frac{\frac{X_1+X_2}{\sqrt{2}}}{\sqrt{\frac{X_3^2+X_4^2+X_5^2}{3}}} \sim t(3) \Rightarrow \frac{\sqrt{3}}{\sqrt{2}} \frac{X_1+X_2}{\sqrt{X_3^2+X_4^2+X_5^2}} \sim t(3)

所以，取 $d=\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{6}}{2}$ 即可，且自由度为 3 .

要深刻理解t分布，就要理解他到底用在哪里，下面的这个例子更好的说明t分布的用途。

t假设检验

例子：假设你在自家花园里种植了西红柿．在过去的几年里，你做了一些观察并发现你种植的西红柿的重量几乎始终服从平均重量为 4 盎司的正态分布。但是，你最近看到了一种新型肥料的广告，它声称可以增加农产品的大小。你突发奇想，决定试一试这种肥料．在你种植的下一批西红柿中，有 2 个 3 盎司的西红柿， 4 个 4 盎司的西红柿，以及 6 个 5 盎司西红柿。据此，你能否断言该肥料会增加产量？

解答：因为我们对肥料能否增加产量感兴趣，所以原假设就是肥料没有影响．用 $\mu$ 表示施肥后西红柿的平均大小，我们有

H_0: \mu \leqslant 4, \quad H_1: \mu>4

与之前一样，假设原假设成立，并令 $\mu=4$ ．为了计算检验统计量，我们需要样本均值和样本方差．不难看出，样本均值为

\bar{x}=\frac{2 \cdot 3+4 \cdot 4+6 \cdot 5}{12}=4.33

样本方差是

s^2=\frac{1}{11}\left(2 \cdot(3-4.33)^2+4 \cdot(4-4.33)^2+6 \cdot(5-4.33)^2\right) \approx 0.61

因此，检验统计量为

\frac{\bar{x}-\mu}{\sqrt{s^2 / n}}=\frac{4.33-4}{0.225} \approx 1.48

这个检验统计量是如何分布的？由于我们使用的是样本方差，所以第一个猜想是 $t$ 分布。但是，要使用 $t$ 分布，我们需要一个基本的正态分布。现在是这样的情况吗？我们说过西红柿的重量几乎服从正态分布，所以由中心极限定理可知，从这个分布中抽取的一个容量为 12 的样本将非常接近于服从正态分布．当然，我们的样本容量比利用中心极限定理的一般情况要小一些，但正态分布的假设看起来是合理的．

因为 $\bar{x}$ 服从正态分布，所以

\frac{\bar{x}-\mu}{\sqrt{s^2 / n}} \sim t_{n-1}

因此，这个检验统计量应该服从一个自由度为 11 的 $t$ 分布．对于这个分布， 1.48 的 $t$ 值对应于一个 0.083 的 $p$ 值．虽然这不是肥料能增加西红柿大小的具体证据，但我可能会一直使用它，直到得出更加有决定性的数据．