4._预测与控制

预测与控制

在一元线性回归问题中, 若回归方程经检验效果显著, 则这时回归值与实际值拟合得较好，因而可以利用它对因变量 $y$ 的新观察值 $y_0$ 进行点预测或区间预测.

预测问题

由于 $x$ 与 $y$ 并非确定性关系，对于任意给定的 $x_0$ ，无法精确知道相应的 $y_0$ 值，但可由回归方程计算出一个回归值 $\hat{y}_0=\hat{\beta}_0+\hat{\beta}_1 x_0$, 以一定的置信度预测对应的 $y$ 的观察值的取值范围,也即对 $y_0$ 做区间估计，即在一定的显著性水平 $\alpha$ 下，寻找一个正数 $\delta$ ，使 $P\left(\left|y_0-\hat{y}_0\right| \leqslant \delta\right)=1-\alpha$, 称区间 $\left[\hat{y}_0-\delta, \hat{y}_0+\delta\right]$ 为 $y_0$ 的概率为 $1-\alpha$ 的预测区间 (Prediction Interval), 这就是所谓的预测问题.

由定理 10.1.1 可推出，

又因 $y_0-\hat{y}_0$ 与 $\hat{\sigma}^2$ 相互独立, 且

所以

故对给定的显著性水平 $\alpha$, 求得

故得 $y_0$ 的置信度为 $1-\alpha$ 的预测区间为

对于给定样本观察值, 可作出曲线

这两条曲线形成包含回归直线 $\hat{y}=\hat{\beta}_0+\hat{\beta}_1 x$ 的带形域, 如图 10.2.1 所示, 这一带形域在 $x=\bar{x}$ 处最窄, 说明越靠近 $\bar{x}$, 预测精度就越高. 而当 $x_0$ 离 $\bar{x}$ 较远时, 置信区域逐渐加宽, 此时精度逐渐下降。

在实际的回归问题中, 当样本容量 $n$ 很大, 并且 $x_0$ 较接近 $\bar{x}$ 时, 有

则 $y_0$ 的置信度为 $1-\alpha$ 的预测区间近似地等于

特别地, 若取 $1-\alpha=0.95$, 则 $y_0$ 的置信度为 0.95 的预测区间为

取 $1-\alpha=0.997$, 则 $y_0$ 的置信度为 0.997 的预测区间为

由此可以预料，在全部可能出现的 $y$ 值中，大约有 $99.7 \%$ 的观测点落在直线 $L_1: y=$ $\hat{\beta}_0-2.97 \hat{\sigma}+\hat{\beta}_1 x$ 与直线 $L_2: y=\hat{\beta}_0+2.97 \hat{\sigma}+\hat{\beta}_1 x$ 所夹的带形区域内, 如图 10.2.2 所示.

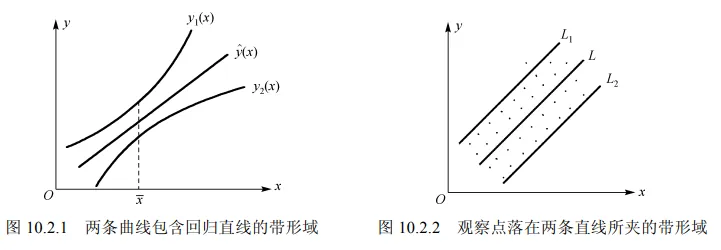
可见，预测区间意义与置信区间的意义相似，只是后者是对未知参数而言的，前者是对随机变量而言的．

例 某建材实验室做陶粒混凝土实验室中，考察每立方米混凝土的水泥用量（kg） 对混凝土抗压强度（kg/ 2 cm ）的影响，测得下列数据．

(1) 求经验回归方程 $\hat{y}=\hat{\beta}_0+\hat{\beta}_1 x$; （2）检验一元线性回归的显著性（ $\alpha=0.05$ ）; (3) 设 $x_0=225 kg$, 求 $y$ 的预测值及置信度为 0.95 的预测区间.

解 (1) $n=12, \bar{x}=205, L_{x x}=14300, \bar{y}=72.6$,

故 $\hat{\beta}_1=L_{x y} / L_{x x}=0.304, \hat{\beta}_0=\bar{y}-\hat{\beta}_1 \bar{x}=10.28$, 得经验回归方程 $\hat{y}=10.28+0.304 x$. (2) $Q_{\text {回 }}=\hat{\beta}_1 L_{x y}=1321.488, Q_{\text {利 }}=L_{y y}-\hat{\beta}_1 L_{x y}=2.332$,

在水平 $\alpha=0.05$ 下, $F_{0.05}(1,10)=4.96$, 因 $F_0>F_{0.05}(1,10)$, 故回归方程显著. (3) $\delta=t_{0.025}(10) \cdot \hat{\sigma} \sqrt{1+\frac{1}{12}+\frac{(225-205)^2}{14300}}=1.054 t_{0.025}(10) \hat{\sigma}$,

则 $\hat{\sigma}=\sqrt{\frac{Q_{\text {利 }}}{n-2}}=\sqrt{\frac{2.332}{10}}=0.4829, t_{0.025}(10)=2.2281$, 故 $\hat{y}_0=10.28+0.304 \times 225=78.68$, 所求预测区间为

控制问题

控制问题是预测问题的反问题，即考虑这样的问题，将观察值 $y$ 控制在一定范围内 $y_1<y<y_2$ 取值，问 $x$ 应控制在什么范围?

对于给定的置信度 $1-\alpha$, 求出相应的 $x_1 、 x_2$, 使 $x_1<x<x_2$ 时, $x$ 所对应的观察值 $y$ 落在 $\left(y_1, y_2\right)$ 之内的概率不小于 $1-\alpha$.

当 $n$ 很大时, 从方程

分别解出 $x$, 作为控制 $x$ 的上、下限:

当 $\hat{\beta}_1>0$ 时, 控制区间为 $\left(x_1, x_2\right)$; 当 $\hat{\beta}_1<0$ 时, 控制区间为 $\left(x_2, x_1\right)$, 如图 10.2.3 所示.

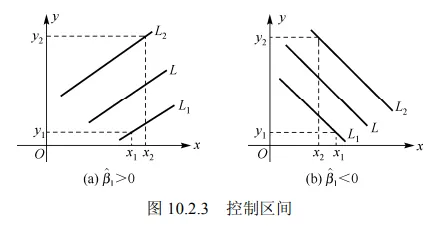
实际应用中, 由式 (10.2.1) 知, 要实现控制, 必须要求区间 $\left(y_1, y_2\right)$ 的长度大于 $2 \hat{\sigma} z_{\alpha / 2}$,否则控制区间不存在.

特别地, 当 $\alpha=0.05$ 时, $z_{\alpha / 2}=z_{0.025}=1.96 \approx 2$, 故式 (10.2.2) 近似为