置信区间定义
设 (X1,X2⋯,Xn) 是来自总体 f(x,θ) 的样本,其中参数 θ∈Θ 末知,对给定 的 0<α<1 ,若存在统计量 θ1(X1,⋯,Xn)≤θ2(X1,⋯,Xn), 使得
P(θ1(X1,⋯,Xn)≤θ≤θ2(X1,⋯,Xn))≥1−α 那么称随机区间 [θ1(X1,⋯,Xn),θ2(X1,⋯,Xn)] 为 θ 的双侧 1−α 置信区间; 称 1−α 为 置信水平;
称 θ1 为 θ 的双侧 1−α 置信区间的下限; 称 θ2 为 θ 的双侧 1−α 置信区间的上限, 简称双侧置信下限或者上限.
抽样以后就得到置信区间的观测值:
[θ1(x1,⋯,xn),θ2(x1,⋯,xn)] 置信区间
置信区间是参数估计的重要内容,下面给他进行简单解释。
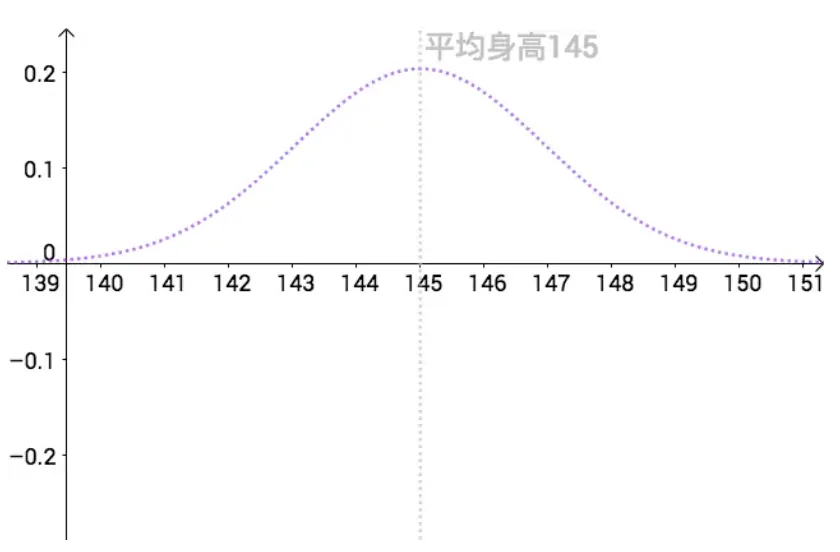
我们通常使用学生的身高来解释置信区间,假设某校学校初中生的身高分布服从如下正态分布 (μ=145,σ=1.4) :
X∼N(145,1.42) 也就是说全校所有同学的平均身高为 145 cm ,为了表示只有上帝可以看到,我把真实分布用虚线来表示:
 {width=450px}
{width=450px}
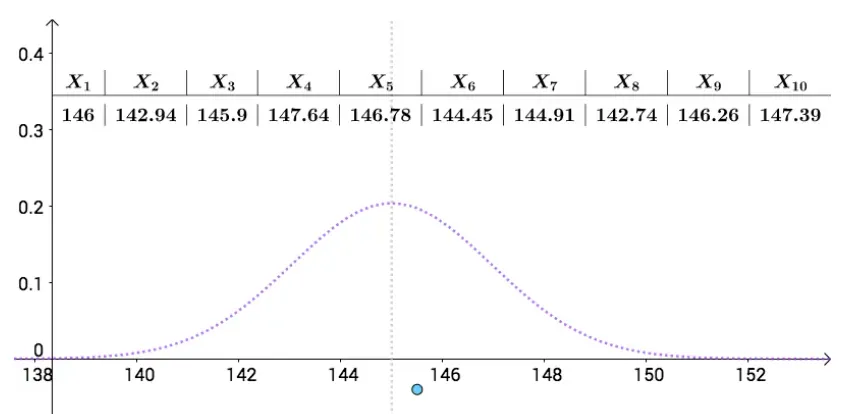
我们不可能把每个学生身高都测量出来,我们只能在人群中抽样统计,比如下面是一次抽样数据,我把算出来的样本均值(记作 μ^ ) 画在图上(蓝色的点):
 {width=450px}
{width=450px}
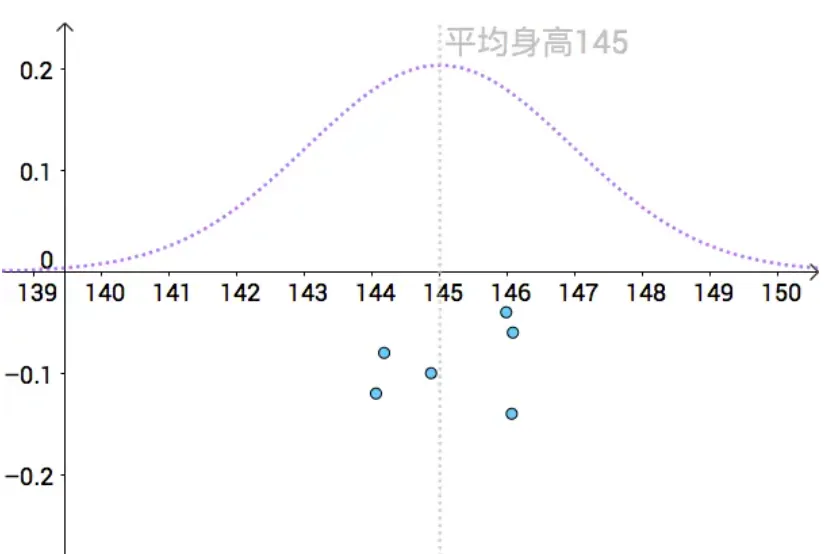
μ^ 就是对真实的 μ 的一次点估计。通过一次次的抽样,我们可以算出不同的身高均值的点估计:
 {width=450px}
{width=450px}
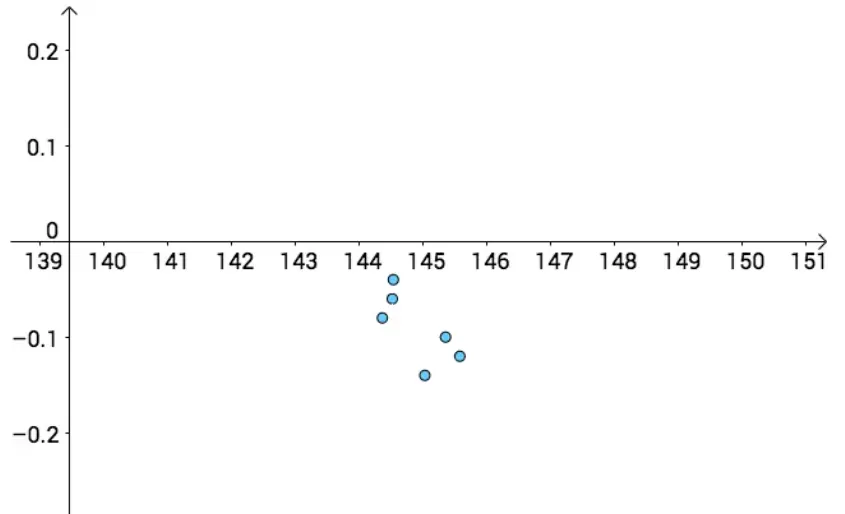
上图是在知道真实值的情况下,关闭上帝的视角,如下图,如果没有真实值,我们其实并不容易分辨不出哪个点估计更好,:
 {width=450px}
{width=450px}
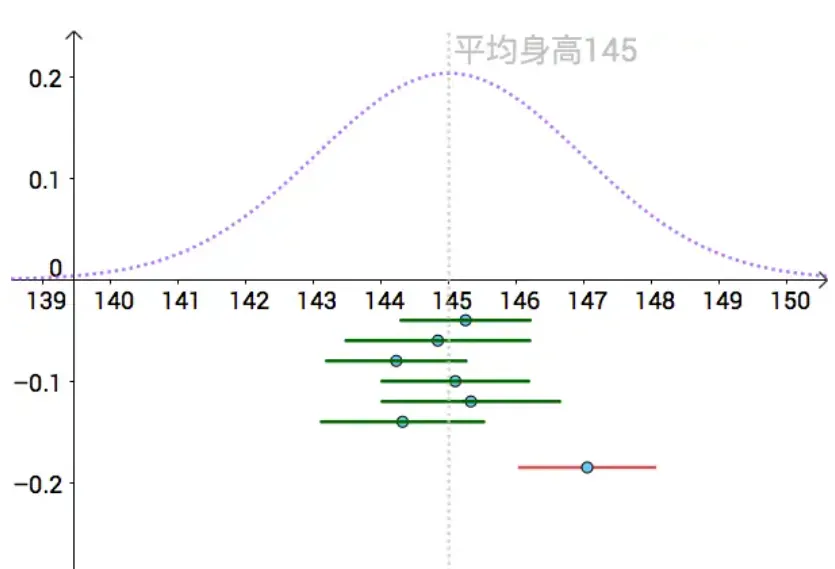
为此提出了置信区间,他提供了一种区间估计的方法。想象一下,我们拿一把尺子,尺子中心点对准采样的样本点,那么尺子左端点和右端点形成一个区间,这个区间称作置信区间。
 {width=450px}
{width=450px}
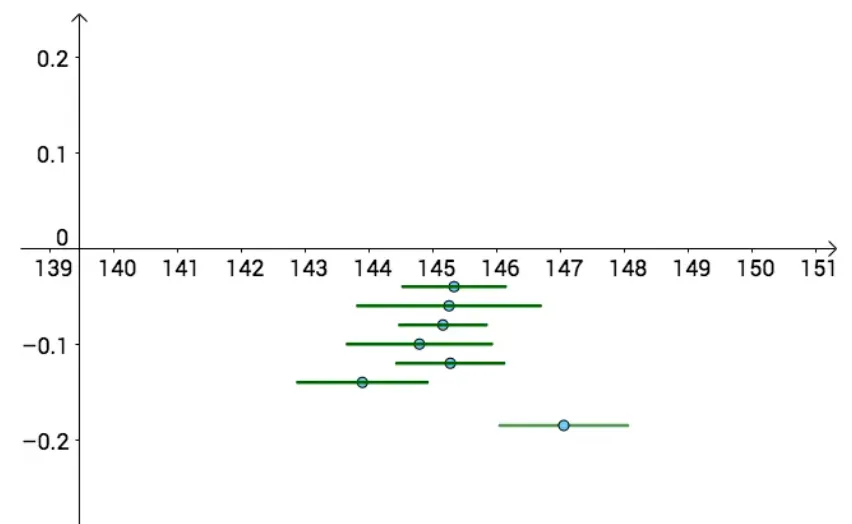
关闭真实值的置信区间是如下的样子。
 {width=450px}
{width=450px}
上图显示有7把“尺子”,在关闭真实值的情况下,我们要从这7把尺子里找到最符合真实值的区间,这就是我们本节要研究的工作。
95%的置信区间估计
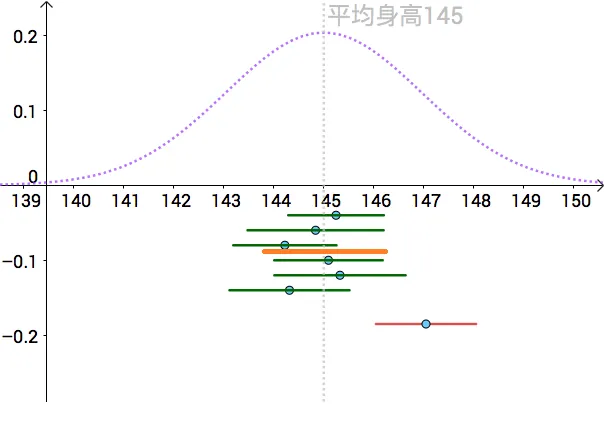
置信区间,提供了一种区间估计的方法。下面采用 95% 置信区间来构造区间估计。如果把每次采样估计的“点”比喻为一条条小鱼,那我们的“网”尽95%的可能性把这些小鱼全网住。如下图的黄色区间尽可能覆盖所有的采样点。
 {width=450px}
{width=450px}
如何构造 95% 置信区间
假设人群的身高服从:
X∼N(μ,σ2) 其中 μ 未知,σ已知。
我们不断对人群进行采样,样本的大小为 n ,样本的均值:
M=nX1+X2+⋯+Xn 根据大数定律和中心极限定律, M服从:
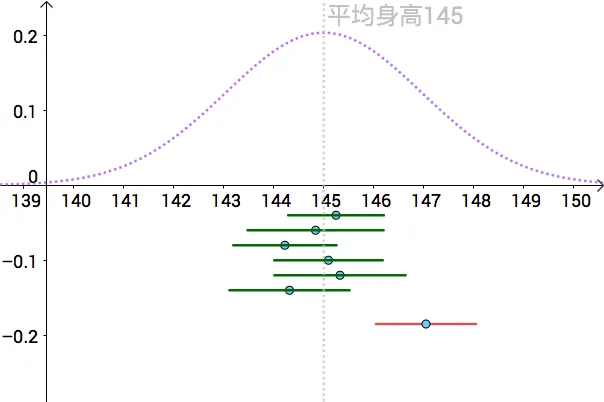
M∼N(μ,nσ2) 我们可以算出以 μ为中心,面积为 0.95的区间,如下图
 {width=450px}
{width=450px}
即:
P(μ−1.96nσ≤M≤μ+1.96nσ)=0.95 (具体推导见下面列子)
也就是, M有 95% 的几率落入此区间:
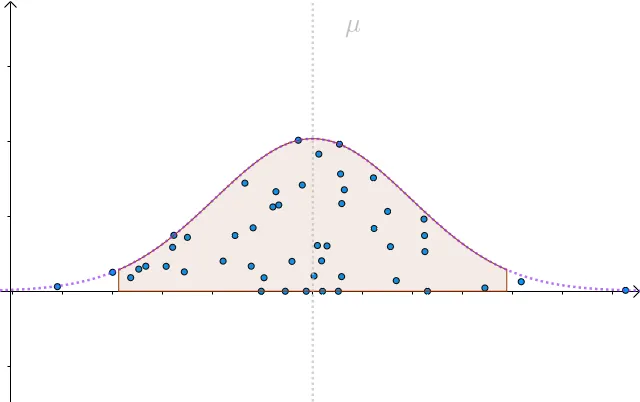 {width=450px}
{width=450px}
那自然,我们以 1.96nσ 为半径做区间,有 95% 的概率把 μ包含进去:
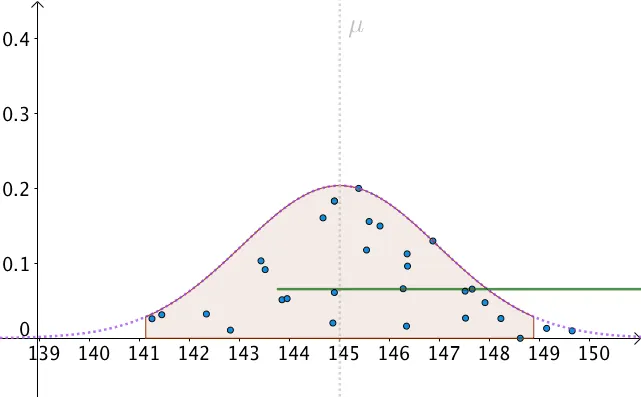 {width=450px}
{width=450px}
那么,只有一个问题了,我们不知道、并且永远都不会知道真实的 μ是多少。
我们就只有用 μ^来代替 μ :
P(μ^−1.96nσ≤M≤μ^+1.96nσ)≈0.95 上面这个公式的推导请参考下面的例1。
例题
例 设 X1,X2,⋯,Xn 为来自正态总体 X∼N(μ,σ2) 的样本,其中 σ2 已知, μ 未知,试求出 μ 的置信度为 1−α 的置信区间.
解:根据点估计知,样本均值 Xˉ 是 μ 的良好估计量,且 根据大数定理与中心极限定理, Xˉ∼N(μ,nσ2) ,把正态分布标准化后,故统计量
U=nσXˉ−μ∼N(0,1). 如图所示,根据标准正态分布上 α 分位点的定义,可得
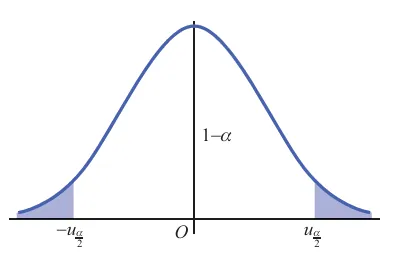
P{−u2α⩽U⩽u2α}=1−α, 即
P{−u2α⩽σ/nXˉ−μ⩽u2α}=1−α 则
P{Xˉ−u2αnσ⩽μ⩽Xˉ+u2αnσ}=1−α 由置信区间的定义可知,[Xˉ−u2αnσ,Xˉ+u2αnσ] 即为 μ 的置信度为 1−α 的置信区间.
注:上面这个例题可以对照下面的例题进行理解。
例 新疆旅游局为调查新疆旅游者的平均消费额,随机访问了 100 名旅游者,得知平均消费额 xˉ=80 元。根据经验,已知旅游者消费服从正态分布,且标准差 σ=12 元,求该地旅游者平均消费额 μ 的置信度为 95% 的置信区间.
分析:本题要求估算旅游者平均消费额多少钱,现在已经知道平均消费80元,这是一个点估计,本题要求给出的是区间估计,结合本题稍后给出的答案,本题可以转换为:我有95%的把握说用户的平均消费金额在77.6∼82.4
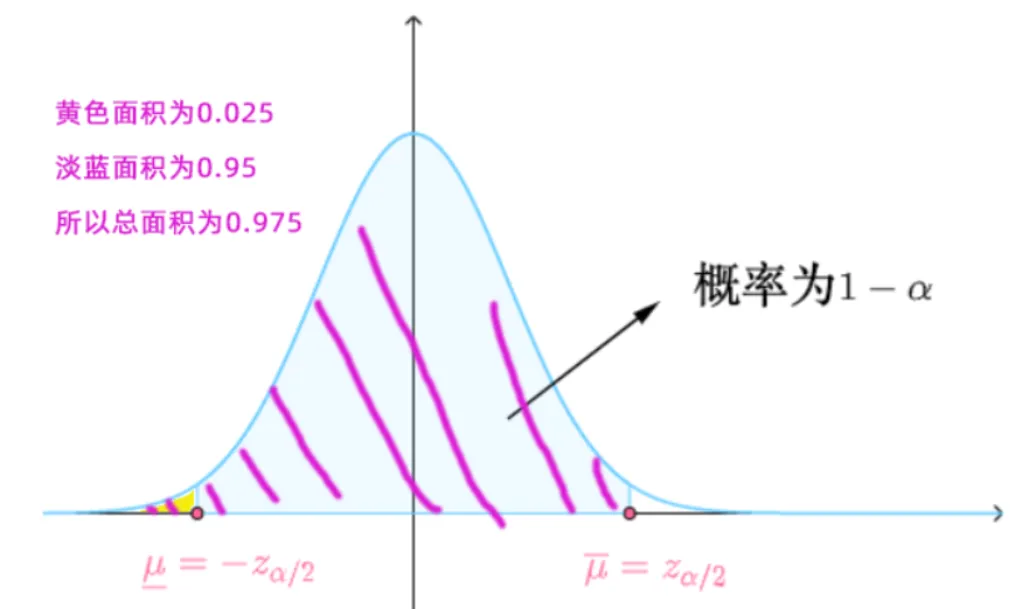
95% 的置信区间就是要求所估计的平均消费金额有95%可能性在下图大的阴影面积里。总概率为1,大的占95%,则剩余的2个黄色面积之和为5%,为了计算方便,我们默认总是把剩余面积一份为二,即左右小的黄色面积各位2.5%
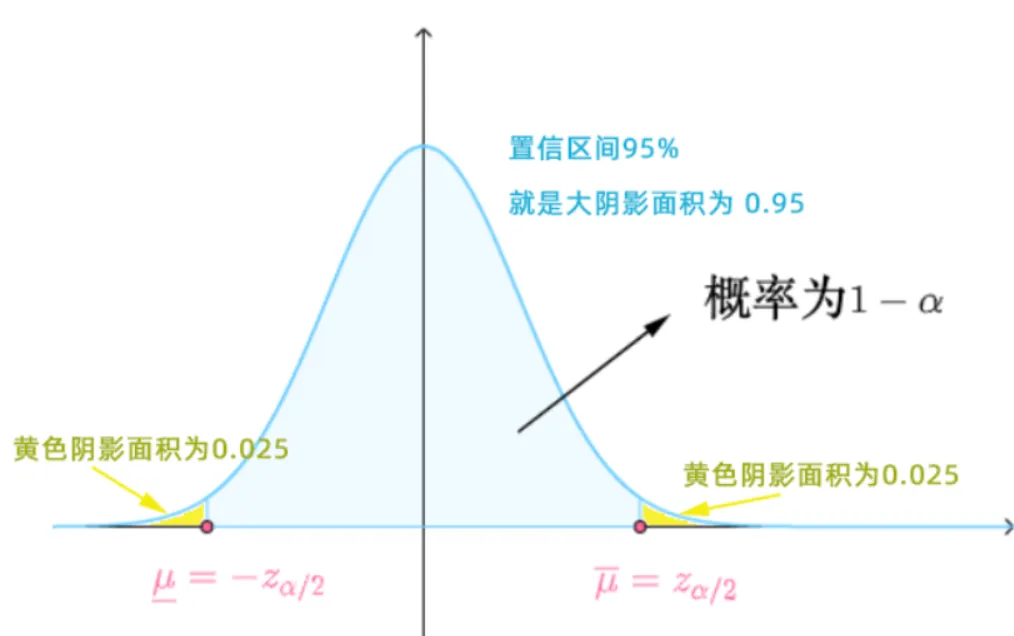 {width=500px}
{width=500px}
因为考试时正态分布表不会给你数据直接查,所以需要进行转换 两旁的黄色面积总和为0.05, 考虑标准正态分布的对称性直接把α除以2, 所以两侧黄色阴影的面积各为2α=0.025
由此可得斜线阴影面积为 0.025+0.95=0.975
 {width=500px}
{width=500px}
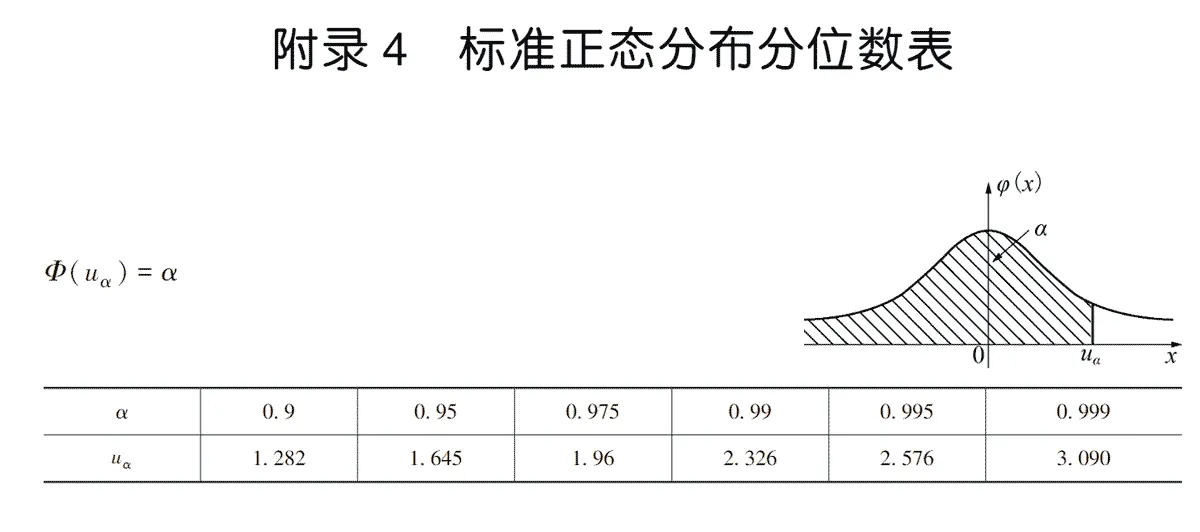
下面把视角切换到正态分布表里。 从正态分布分位数表可以看到当ua=1.96 时,阴影面积正好为0.975.
上面这个结论最好记住:当正态分布估计量上下浮动±1.96时,此时具有 95% 的可信度,这是一个常用的结论
 {width=600px}
{width=600px}
解:
对于给定的置信度
1−α=0.95 可知
α=0.05,α/2=0.025 查标准正态分布表得
附录给出了 标准正态分布分位表
u0.025=1.96 由
n=100,xˉ=80,σ=12,u0.025=1.96 计算得
xˉ−uα/2⋅nσ=80−1.96∗1012=82.4=77.6,xˉ+uα/2⋅nσ=80+1.96∗1012=82.4, 所以 μ 的置信度为 95% 的置信区间为 (77.6,82.4) ,
即在已知误差为 σ=12 的情形下,可以 95% 的置信度认为每个旅游者的平均消费额在 77.6∼82.4 元范围内.
扩展本题
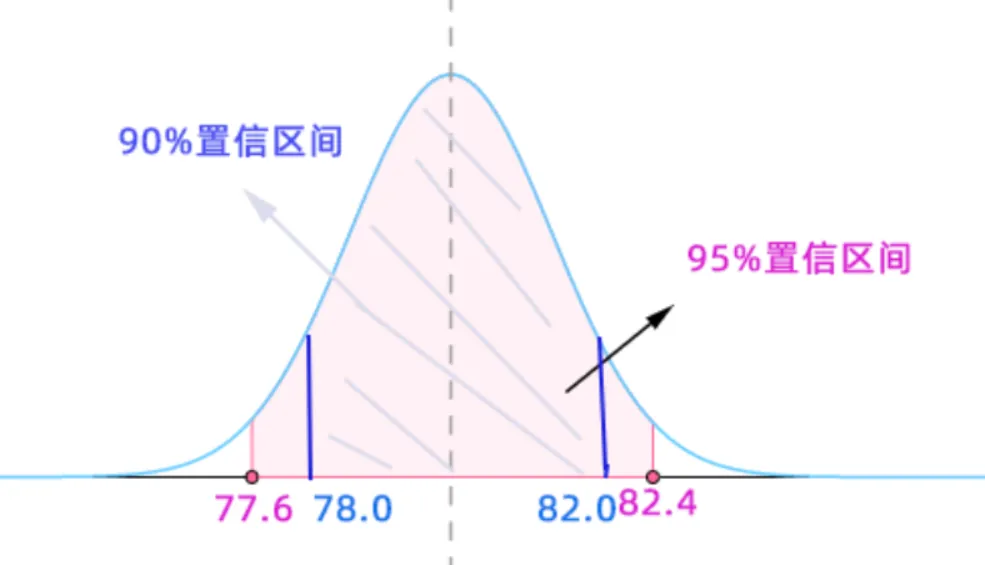
如果本题要求有90%的置信区间呢?此时阴影面积为0.9+0.05=0.95,查表得ua=1.645
计算得
xˉ−uα/2⋅nσ=80−1.645∗1012=82.4=78.0xˉ+uα/2⋅nσ=80+1.645∗1012=82.0 对结果解读:
如果领导问你,游客平均消费多少呀?你可以回答,我有95%的把握说用户消费金额在77.6∼82.4 之间,如果希望更精确的消费答案,我有90%的把握说用户消费金额在 78.0∼82.0之间。从本题还可以看到,因为后者限定的范围更小,导致我在估算时的保证度降低,所以需要理解其中的含义。
 {width=500px}
{width=500px}
注意:下面这题可以等学完了 单个正态总体的参数的区间估计 再来理解。
例 新疆旅游局随机访问了 25 名旅游者,得知平均消费额 xˉ=80 元,样本标准差 s=12 元,已知旅游者消费额服从正态分布,求旅游者平均消费额 μ 的 95% 置信区间.
解 对于给定的置信度
1−α=0.95 可知
α=0.05,α/2=0.025, 查表得
tα/2(n−1)=t0.025(24)=2.0639, 由
xˉ=80,s=12,n=25,t0.025(24)=2.0639, 计算得
xˉ−tα/2(n−1)⋅ns=75.05,xˉ+tα/2(n−1)⋅ns=84.95 所以 μ 的置信度为 95% 的置信区间为 (75.05,84.95) ,即在 σ2 未知的情况下,估计每个旅游者的平均消费额在 75.05∼84.95 元范围内,这个估计的可靠度是 95% .
总结
对此例进行分析,我们发现随机变量 U 在置信区间的构造过程中起着关键作用,它具有下列特点:
(1)是待估参数 μ 和估计量 Xˉ 的函数;
(2)不含其他未知参数;
(3)其分布已知且与未知参数 μ 无关。
我们称满足上述 3 条性质的量 Q 为枢轴量。
在引入枢轴量 Q 的概念后,我们归纳出求置信区间的一般步骤如下:
(1)根据待估参数构造枢轴量 Q ,一般可由未知参数的良好估计量改造得到;
(2)对于给定的置信度 1−α ,利用枢轴量 Q 的分位点确定常数 a 和 b ,使
P{a⩽Q⩽b}=1−α (3)将不等式恒等变形为
P{θ^1⩽θ⩽θ^2}=1−α 即可得到参数 θ 的置信度为 1−α 的置信区间 [θ^1,θ^2] .
置信上下限
同等置信区间定义1
如对给定的 α(0<α<1), 对任意的 θ∈Θ, 有
Pθ(θ^1⩽θ⩽θ^2)=1−α, 则称 [θ^1,θ^2] 为 θ 的 1−α 同等置信区间.
在一些实际问题中, 人们感兴趣的有时仅仅是未知参数的一个下限或一个上限.譬如, 对某种产品的平均寿命来说, 我们希望它越大越好, 因此人们关心的是它的 0.90置信下限是多少, 此下限标志了该产品的质量, 它的一般定义如下.
置信上限定义2
若有统计量 θˉ=θˉ(X1,⋯,Xn) ,使得 Pθ(θ≤θˉ)≥1−α,θ∈Θ 则称 (−∞,θˉ(X1,⋯,Xn)] 为 θ 的单侧 1−α 置信区间, θˉ(X1,⋯,Xn) 为 θ 的单侧 1−α 置信上限.
置信下限定义3
若有统计量 θ=θ(X1,⋯,Xn) ,使得 Pθ(θ≥θ)≥1−α,θ∈Θ 则称 [θ(X1,⋯,Xn),+∞) 为 θ 的单侧 1−α 置信区间, θ(X1,⋯,Xn) 为 θ 的单侧 1−α 置信下限.
 {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px} {width=450px}
{width=450px}
 {width=500px}
{width=500px} {width=500px}
{width=500px} {width=600px}
{width=600px} {width=500px}
{width=500px}