3._按分布收敛

按分布收敛

分布函数全面描述了随机变量的统计规律，因此讨论随机变量分布函数序列 {F(xn)}\left\{F\left(x_n\right)\right\} 的收敛有重要的意义。

定义 设随机变量 X,X1,X2,⋯X, X_1, X_2, \cdots 的分布函数分别为 F(x),F1(x),F2(x),⋯F(x), F_1(x), F_2(x), \cdots ．若对 F(x)F(x) 的任意连续点 xx ，都有

lim⁡n→∞Fn(x)=F(x)\lim _{n \rightarrow \infty} F_n(x)=F(x)

则称 {Fn(x)}\left\{F_n(x)\right\} 弱收敛于 F(x)F(x) ，记为 Fn(x)→WF(x)F_n(x) \xrightarrow{W} F(x) 。也称 {Xn}\left\{X_n\right\} 按分布收敛于 XX ，记为 Xn→LXX_n \xrightarrow{L} X ． 依概率收敛与弱收敛之间有什么关系呢？下面定理给出依概率收敛是比弱收敛更强的收敛。

定理 Xn→PX⇒Xn→LX\quad X_n \xrightarrow{P} X \Rightarrow X_n \xrightarrow{L} X ． 证明 略。 上面定理说明了若随机变量序列 {Xn}\left\{X_n\right\} 依概率收敛于 XX ，则一定按分布收敛于 XX ．反之，不一定成立。那么在什么情况下，这两种收玫等价呢？下面定理给出了两种收玫等价的条件。

定理 若 cc 为常数，则 Xn→PcX_n \xrightarrow{P} c 的充要条件是 Xn→LcX_n \xrightarrow{L} c ． 证明 略．

按分布收敛的通俗解释

事实上, 这是最弱的一种收敛, 它蕴含在其他所有类型的收敛中. 我们来看个例子．设 XnX_n 是一个服从均匀分布的随机变量，其概率密度函数为

fn(x)={1n 若 x∈{0,1n,2n,⋯ ,n−2n,n−1n}0 其他. f_n(x)= \begin{cases}\frac{1}{n} & \text { 若 } x \in\left\{0, \frac{1}{n}, \frac{2}{n}, \cdots, \frac{n-2}{n}, \frac{n-1}{n}\right\} \\ 0 & \text { 其他. }\end{cases}

下标 nn 是为了强调我们有 nn 个非零值，这些值是均匀间隔的， 如下图(n=10n=10)

图片

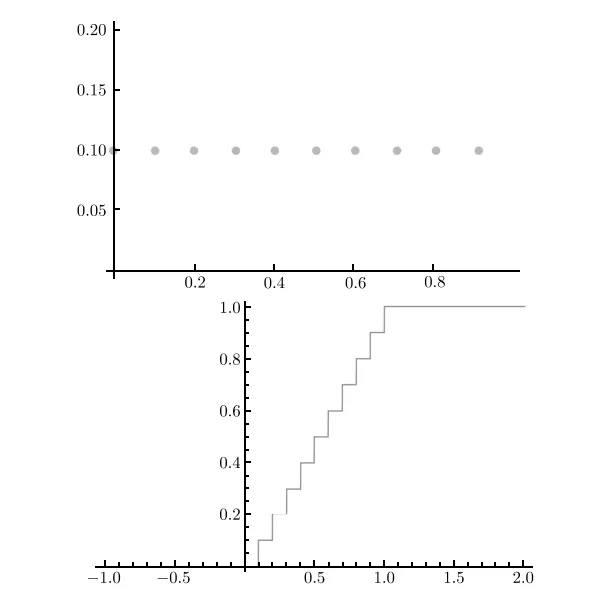
从概率密度函数中不难看出，对于任意的 x∈[0,1]x \in[0,1] ，都有 lim⁡n→∞fn(x)=0\lim _{n \rightarrow \infty} f_n(x)=0 ．考察这一点最简单的方法是，除了 nn 个特殊值外，fn(x)=0f_n(x)=0 对其余所有 xx均成立．当 xx 取任意特殊值时，fn(x)f_n(x) 都等于 1/n1 / n 。随着 nn 的增加，这个值会减小到 0 。

分布函数的情况则截然不同．当 x∈[0,1]x \in[0,1] 时，Fn(x)F_n(x) 等于 1n\frac{1}{n} 乘以 {0,1/n,2/n,⋯\{0,1 / n, 2 / n, \cdots ， (n−1)/n}(n-1) / n\} 中不大于 xx 的值的个数。这是因为 分布函数 等于随机变量不大于 xx的概率．对于任意的 x∈[0,1]x \in[0,1] ，

Fn(x)=∑0⩽k⩽n−1k/n⩽x1n=⌊nx⌋n,F_n(x)=\sum_{\substack{0 \leqslant k \leqslant n-1 \\ k / n \leqslant x}} \frac{1}{n}=\frac{\lfloor n x\rfloor}{n},

其中，函数 ⌊y⌋\lfloor y\rfloor 表示不超过 yy 的最大整数．因为 ⌊y⌋\lfloor y\rfloor 与 yy 最多相差 1 ，所以 nx−1⩽⌊nx⌋⩽nxn x-1 \leqslant\lfloor n x\rfloor \leqslant n x ，于是有

x−1n⩽Fn(x)⩽xx-\frac{1}{n} \leqslant F_n(x) \leqslant x

当取极限 n→∞n \rightarrow \infty 时， lim⁡n→∞Fn(x)=x\lim _{n \rightarrow \infty} F_n(x)=x ．这正是服从 [0,1][0,1] 上均匀分布的随机变量的累积分布函数。

我们看到了这种收敛被称为弱收敛的原因：概率密度函数没有收敛到均匀分布的概率密度函数。乍一看，这应该会令人感到失望，但是从很多方面来说还不算太糟。回想一下，我们可以利用分布函数来计算事件的概率．

Previous2._依概率收敛
Next4._马尔可夫不等式