6._离散型_二项分布 - Probability Theory and Mathematical Statistics

抽查一个产品，质量可能合格或者不合格，这是两点分布。单纯抽查一次作用不大，可以抽查多次(需要放回)，这就是本节介绍的二项分布。

设对一随机试验 $\mathrm{E}$ ，我们只关心某个事件 $A$ 发生与否，此时试验的结果可以看成只有两种: $A$ 发生或者 $A$ 不发生。那么称这个试验为伯努利试验.

接下来将引入二项分布，考察二项分布的方法有两种．

方法一：我们可以每次拋掷一枚硬币，然后记录正面出现的次数，然后抛掷 $n$ 次。

方法二：我们有 $n$ 枚独立的硬币，并且每一枚硬币出现成功的概率都是 $p$ 。把他一次性的放在手里同时抛郑它们，并记录正面出现的次数。

这两种观点都很有用。很明显，在抛掷硬币的实验里，第一次抛掷的结果不影响第二次抛掷的结果，所以我们假设了硬币的独立性，因此这两种看法是等价的。即一次抛掷 $n$ 枚硬币与抛郑一枚硬币 $n$ 次没什么区别。

解读方法一

现在我们使用方法一对二项分布进行举例。假设车间生产了一批产品，其中 $a$ 个是合格的， $b$ 个是不合格的。我们用 $A$ 表示＂取到产品是合格的＂，那么一次检测中，合格率为 $P(A)=\dfrac{a}{a+b}$ 。

若连续检测 $n$ 个产品（需要放回）抽样，这就是 $n$ 重伯努利试验。

以 $X$ 表示 $n$ 重伯努利试验中事件 $A$ 发生的次数， $X$ 是一个随机变量，我们来求它的分布律． $X$ 所有可能取的值为 $0,1,2, \cdots, n$ ．由于各次试验是相互独立的，

因此事件 $A$ 在指定的 $k(0 \leqslant k \leqslant n)$ 次抽查中发生，在其他 $n-k$ 次试验中 $A$ 不发生的概率为：

\begin{aligned} \underbrace{p \cdot p \cdot \cdots \cdot p}_{k \uparrow} \cdot \underbrace{(1-p) \cdot(1-p) \cdot \cdots \cdot(1-p)}_{n-k \uparrow}=p^k(1-p)^{n-k} . \end{aligned}

这种指定的方式共有 $C_n^k$ 种，它们是两两互不相容的，故在 $n$ 次试验中 $A$ 发生 $k$ 次的概率为 $C_n^k p^k(1-p)^{n-k}$ ，记 $q=1-p$ ，即有

P\{X=k\}= C_n^k p^k q^{n-k}, k=0,1,2, \cdots, n .

解读方法二

现在我们对上面的例子用方法二进行解读：有3个产品，每个产品都有合格和不合格两种可能，那么，这3个产品的结果可以记为 $(0,0,0),(0,0,1),(0,1,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,1)$ 共 $2^3=8$ 种可能。

其中 $(0,0,0)$ 表示 $3$ 个产品都不合格， $(1,1,1)$ 表示 $3$ 个产品都合格，而 $(0,0,1)$ 表示第一个第二个不合格，第三个合格。

以此类推，因为 $n$ 重伯努利试验的基本结果可以记作

X=\left(x_1, x_2, \cdots, x_n \right),

其中 $x_i$ 的值为 $A$ , 或者为 $\bar{A}$ . 这样的 $\omega$ 共有 $2^n$ 个, 这 $2^n$ 个样本点 $\omega$ 组成了样本空间 $\Omega$ .

求 $X$ 的分布列, 即求事件 $\{X=k\}$ 的概率. 若某个样本点

X=\left(x_1, x_2, \cdots, x_n \right) \in\{X=k\}

意味着 $x_1, x_2, \cdots, x_n$ 中有 $k$ 个 $A, n-k$ 个 $\bar{A}$ , 所以由独立性知,

P(x)=p^k(1-p)^{n-k} .

而事件 $\{X=k\}$ 中这样的 $x$ 共有 $C_n^k$ 个, 所以 $X$ 的分布列为

P(X=k)=C_n^k p^k(1-p)^{n-k}, k=0,1, \cdots, n .

这个分布称为二项分布, 记为 $X \sim B(n, p)$ .

下面给出具体的定义

组合里，组合记法有苏联式记法和美国式记法。苏式记法是 $C_n^m$ 而美式记法 $\left(\begin{array}{l}n \\ m\end{array}\right)$ , 详见此处

二项分布定义

若随机变量 $X$ 的分布律为

P(X=k)=C_n^k p^k(1-p)^{n-k}, \quad k=0,1, \cdots, n,

则称 $X$ 服从参数为 $n 、 p$ 的二项分布（Binomial Distribution）, 记为 $X \sim B(n, p)$ .

当 $n=1$ 时, 二项分布就是上节介绍的 $(0-1)$ 分布, 故 $(0-1)$ 分布的分布律也可写成

P(X=k)=p^k q^{1-k},

其中 $q=1-p, k=0,1$ .

在使用二项分布 $X \sim B(n, p)$ 时，一定要明白哪个是 $n$ ，哪个是 $p$ , 记法里 $n$ 是实验次数， $p$ 是发生概率。

例某特效药的临床有效率为 0.95 , 今有 10 人服用, 问至少有 8 人治愈的概率是多少? 解设 $X$ 为 10 人中被治愈的人数, 则 $X \sim B(10,0.95)$ , 而所求概率为

\begin{aligned} P(X \geqslant 8) & =P(X=8)+P(X=9)+P(X=10) \\ & =C_{10}^8 0.95^8 0.05^2+C_{10}^9 0.95^9 0.05+C_{10}^{10} 0.95^{10} \\ & =0.0746+0.3151+0.5987=0.9884 . \end{aligned}

10人种至少8人被治愈的概率为 0.9884

应用场景

二项分布是一种常用的离散分布,譬如,

检查 10 件产品, 10 件产品中不合格品的个数 $X$ 服从二项分布 $b(10, p)$ , 其中 $p$ 为不合格品率.
调查 50 个人, 50 个人中患色盲的人数 $Y$ 服从二项分布 $b(50, p)$ , 其中 $p$ 为色盲率.
射击 5 次, 5 次中命中次数 $Z$ 服从二项分布 $b(5, p)$ , 其中 $p$ 为射手的命中率.

通俗理解二项方便

掷一枚硬币出现正面和反面的概率各为 0.5 ，那么掷 1 次，出现正面的概率肯定是0．5。掷2次、掷3次呢？

掷 2 次出现的结果有 4 个，正正、正反、反正、反反。因为 $p =0.5$ ，所以每个结果出现的概率是 $0.5 \times 0.5=0.25$ ，那正面出现 2 次、 1 次、 0 次的概率分别是 $0.25 、 0.5 、 0.25$ 。

掷 3 次出现的结果有 8 个，正正正、正正反、正反正、正反反、反正正、反正反、反反正、反反反。每个结果出现的概率是 $0.5 \times 0.5 \times 0.5=0.125$ ，那正面出现 3 次、 2 次、 1 次、 0 次的概率分别是 $0.125 、 0.375 、 0.375 、 0.125$ 。

统计学家们总结出了计算概率的一般公式

b(x, n, p)=C_n^x p^x q^{n-x}

其中 $b$ 表示二项分布的概率， $n$ 表示试验次数， $x$ 表示出现某个结果的次数，是组合，表示在 $n$ 次试验中出现 $x$ 次结果的可能的次数。如 10 次试验，出现 0 次正面的次数有 1 次，出现 1 次正面的次数有 10 次，等等。其计算也有一个通式：

C_n^x=\frac{n \times(n-1) \times \cdots \times(n-x+1)}{x \times(x-1) \times \cdots \times 1}

例题

例人向同一目标重复独立射击5次，每次命中目标的概率为 $0.8$ ，求 (1) 此人能命中3次的概率；（2）此人至少命中2次的概率。解：设 $X$ 表示在5次重复独立射击中命中的次数，则

X \sim B(5,0.8)

1 $P(X=3)=\left(\begin{array}{l}5 \\ 3\end{array}\right) \times 0.8^3 \times 0.2^2=0.2048$ $2 \quad P(X \geq 2)=1-P(X<2)=1-P(X=0)-P(X=1)=0.99328$

例设有 80 台同类型设备, 各台工作是相互独立的, 发生故障的概率都是 0.01 ,且一台设备的故障能由一个人处理。考虑两种配备维修工人的方法：其一是由 4 人维护，每人负责 20 台；其二是由 3 人共同维护 80 台。试比较这两种方法在设备发生故障时不能及时维修的概率。

解按第一种方法。以 $X$ 记 "第 1 人维护的 20 台中同一时刻发生故障的台数"，以 $A_i(i=1,2,3,4)$ 表示 "第 $i$ 人维护的 20 台中发生故障不能及时维修"，则知 80 台中发生故障不能及时维修的概率为

P\left(A_1 \cup A_2 \cup A_3 \cup A_4\right) \geqslant P\left(A_1\right)=P(X \geqslant 2) .

而 $X \sim B(20,0.01)$ , 故有

\begin{aligned} P(X \geqslant 2) & =1-P(X=0)-P(X=1) \\ & =1-C_{20}^0 \times(0.01)^0 \times(0.99)^{20}-C_{20}^1 \times(0.01)^1 \times(0.99)^{19} \\ & =0.0169 . \end{aligned}

即

P\left(A_1 \cup A_2 \cup A_3 \cup A_4\right) \geqslant 0.0169 .

按第二种方法. 以 $Y$ 记 80 台中同一时刻发生故障的台数. 此时 $Y \sim B(80,0.01)$ , 故 80 台中发生故障而不能及时维修的概率为

P(Y \geqslant 4)=1-\sum_{k=0}^3 C_{80}^k \times(0.01)^k \times(0.99)^{80-k}=0.0087

结果表明，后一种情况尽管任务重了（每人平均维护约 27 台），但工作效率不仅没有降低, 反而提高了。

例设在 3 次重复独立试验中，事件 $A$ 出现的概率都相等．已知 $A$ 至少出现一次的概率为 $\frac{19}{27}$ ．试求事件 $A$ 在一次试验中出现的概率。

解设 $X$ 表示事件 $A$ 出现的次数．由已知，得 $X \sim B(3, p)$ ，其中 $p=P(A)$ ．因为 $P\{X \geqslant 1\}=1-P\{X=0\}=1- C _3^0 p^0(1-p)^3=\frac{19}{27}$ ，所以 $p=\frac{1}{3}$ ．故 $P(A)=p=\frac{1}{3}$ ．

例金工车间有 10 台同类型的机床，每台机床配备的电动机功率为 10 kW ，已知每台机床工作时，平均每小时实际开动 12 min ，且开动与否是相互独立的．现在当地电力供应紧张，供电部门只提供 50 kW 的电力给这 10 台机床，问：这 10 台机床能够正常工作的概率是多大？

解设 $X$ 表示 10 台机床中同时开动的台数。由题意知，每台机床分为＂开动＂和＂不开动＂两种情况，开动的概率为 $\frac{12}{60}=\frac{1}{5}$ ，每台机床开动与否相互独立，则 $X \sim B\left(10, \frac{1}{5}\right)$ ，其分布律为

P\{X=k\}=\mathrm{C}_{10}^k\left(\frac{1}{5}\right)^k\left(\frac{4}{5}\right)^{10-k}, \quad k=0,1,2, \cdots, 10 .

根据题意，若同时开动的台数不超过 5 台，这 10 台机床就能正常工作，其概率为

P\{X \leqslant 5\}=\sum_{k=0}^5 \mathrm{C}_{10}^k\left(\frac{1}{5}\right)^k\left(\frac{4}{5}\right)^{10-k} \approx 0.994 .

因此，这 10 台机床能够正常工作的概率为 0.994 ，说明这 10 台机床的工作基本上不受电力供应紧张的影响。

例有 2500 个相同年龄阶段、相同社会层次的人购买了某保险公司的意外伤害保险，根据以往统计资料，在一年里每个人出现意外伤害的概率是 0.0001 ，每个购买保险的人一年付给保险公司 120 元保费，而在出现意外伤害时家属从保险公司领取 2 万元。请计算：（1）保险公司亏本的概率；（2）保险公司一年获利不少于 10 万元的概率．

解 2500 人中出现意外伤害的情况可以用 2500 重伯努利试验描述，设 $X$ 表示 2500 人中出现意外伤害的人数，则出现意外伤害的人数是 $k$ 的概率为

P\{X=k\}=\mathrm{C}_{2500}^k 0.0001^k(1-0.0001)^{2500-k}, k=0,1,2, \cdots, 2500

保险公司每年从这 2500 人收取的保费为

2500 \times 120=300000 \text { (元). }

（1）根据前面的分析可知，只有超过 15 人出现意外伤害时保险公司才亏本，保险公司亏本的概率为

P\{X>15\}=\sum_{k=16}^{2500} \mathrm{C}_{2500}^k 0.0001^k 0.9999^{2500-k} \approx 0.000001

（2）只要不多于 10 人出现意外伤害，保险公司可以至少赚 10 万元，因此，保险公司一年获利多于 10 万元的概率为

P\{X \leqslant 10\}=\sum_{k=0}^{10} \mathrm{C}_{2500}^k 0.0001^k 0.9999^{2500-k} \approx 0.999994

在二项分布概率的计算中，经常会遇到例 2.6 这样的和式比较大、计算比较困难的情况，这种问题该如何解决呢？可以用泊松分布进行近似计算，也就是下面将要介绍的泊松定理的内容．

二项分布的数学期望和方差

设随机变量 $X \sim B(n, p)$ , 则

\begin{aligned} E(X) & =\sum_{k=0}^n k\binom{n}{k} p^k(1-p)^{n-k}=n p \sum_{k=1}^n\binom{n-1}{k-1} p^{k-1}(1-p)^{(n-1)-(k-1)} \\ & =n p[p+(1-p)]^{n-1}=n p . \end{aligned}

又因为

\begin{aligned} E\left(X^2\right) & =\sum_{k=0}^n k^2\binom{n}{k} p^k(1-p)^{n-k}=\sum_{k=1}^n(k-1+1) k\binom{n}{k} p^k(1-p)^{n-k} \\ & =\sum_{k=1}^n k(k-1)\binom{n}{k} p^k(1-p)^{n-k}+\sum_{k=1}^n k\binom{n}{k} p^k(1-p)^{n-k} \\ & =\sum_{k=2}^n k(k-1)\binom{n}{k} p^k(1-p)^{n-k}+n p \\ & =n(n-1) p^2 \sum_{k=2}^n\binom{n-2}{k-2} p^{k-2}(1-p)^{(n-2)-(k-2)}+n p \\ & =n(n-1) p^2+n p . \end{aligned}

由此得 $X$ 的方差为

D(X)=E\left(X^2\right)-(E(X))^2=n(n-1) p^2+n p-(n p)^2=n p(1-p) .

因此，二项分布的数学期望是 $np$ ，方差是 $np(1-p)$

关于更多概率分布表见附录1：常见概率分布表

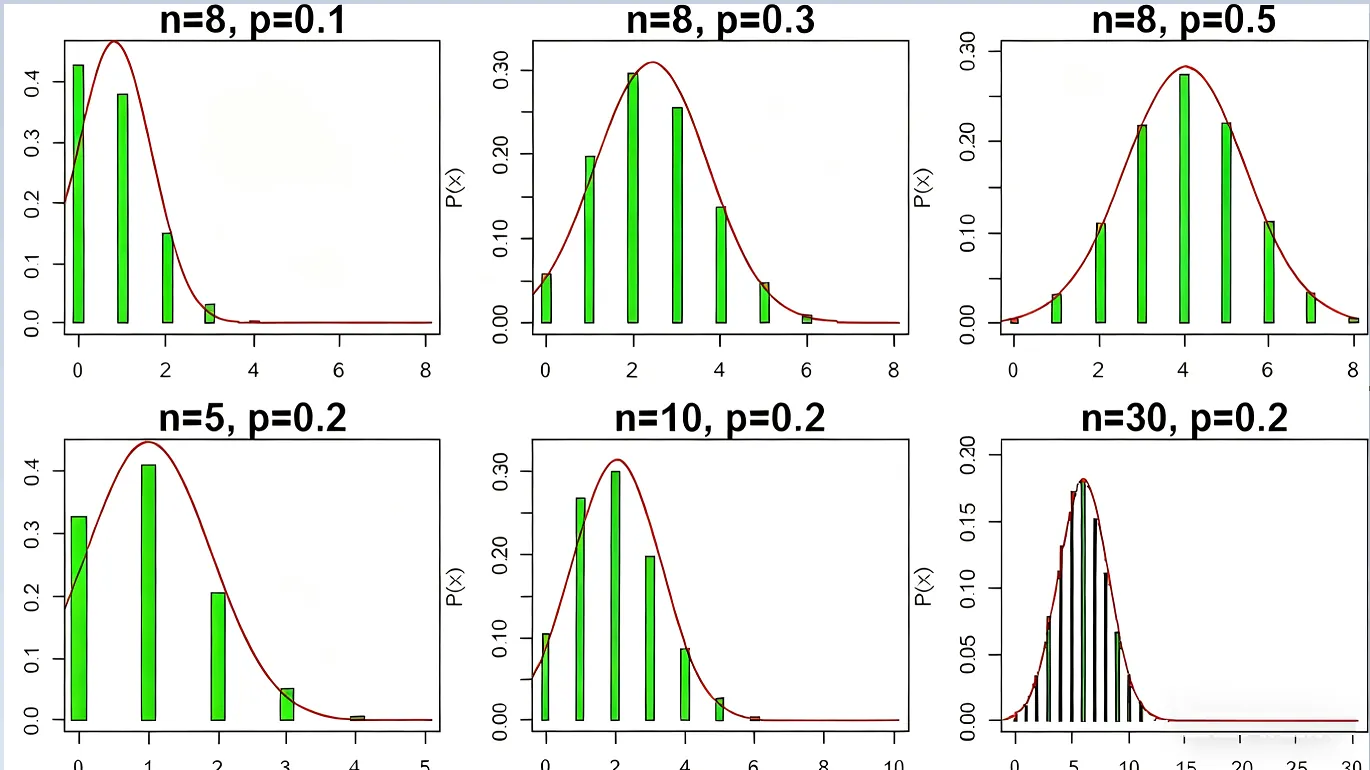
二项分布图像参数关系

二项分布的另一个性质是其分布形状的变化规律。从二项分布概率质量函数P(x)可知，概率分布只与试验次数n和成功概率p有关，其分布形状的变化规律为：

"成功"概率p越接近0.5(也即"成功"概率与"失败"概率越接近)，二项分布将越对称。保持二项分布试验的次数n不变，随着成功概率p越接近0.5，二项分布逐渐对称，且近似于均值为np、方差为npq的正态分布。(见下图的第一排3个子图)

对于任意"成功"概率p，无论其距离0.5有多远，随着试验次数n的增加，二项分布与均值为np、方差为npq的正态分布越来越接近。(见下图的第二排3个子图)

以上两个二项分布形状变化规律，可明显由下图观察出来。图中的横轴代表试验"成功"的次数；纵轴代表次数对应的概率；红线是均值为np、方差为npq的正态分布曲线。

后续再介绍大数定律里,会介绍二项分布的正态估计,利用的就是这个性质,详见二项分布正态估计

在下图第一排的3张图片里可以这么理解,假设一台机器每天发生故障的概率为 $50\%$ ，那么8天时间里，发生故障的天数就是 $8*0.5=4$ , 同样，如果机器每天故障发生的概率为 $10\%$ ,8天里差不多有 $8*0.1=0.8$ 天发生故障。

在第二排图片里，假设机器每天发生故障概率为 $20 \%$ , 那么观察的次数越多，就会发现，故障多发生在期望值附近符合正态分布，比如在一个月里（30天），有50%的概率会发生4-8次的故障，而每月故障超过10次或者低于2次的概率都非常少。

$图片$

赌徒效应

有一个赌博问题．假设庄家要抛掷 4 颗独立的骰子，玩家可以对 1 到 6 的任意一个数字下注．如果下注的数字出现了 $k$ 次，那么玩家就赢得了 $k$ 美元，其中 $k$ 在 1 和 4 之间取值．如果该数字没有出现，那么玩家将损失 1 美元．玩家应该玩这个游戏吗？

为了弄清楚该不该玩，我们想知道预期结果．这个词提醒了我们应该计算什么．如果多次玩这个游戏，那么会赢钱还是会输钱？这个问题可以通过计算期望值来回答．如果让 $X$ 表示当抛掷 4 颗独立的均匀骰子时赢得或损失的钱数，那么 $X$ 的可能取值有：-1 （下注的数字出现了 0 次）， 1 （下注的数字出现了 1 次）， 2 （下注的数字出现了 2 次） $\cdots \cdots 4$ ．现在我们计算每一种情况发生的概率：

\begin{aligned} \operatorname{Prob}(X=-1) & =\binom{4}{0}\left(\frac{1}{6}\right)^0\left(\frac{5}{6}\right)^4=\frac{625}{1296} \\ \operatorname{Prob}(X=1) & =\binom{4}{1}\left(\frac{1}{6}\right)^1\left(\frac{5}{6}\right)^3=\frac{125}{324} \\ \operatorname{Prob}(X=2) & =\binom{4}{2}\left(\frac{1}{6}\right)^2\left(\frac{5}{6}\right)^2=\frac{25}{216} \\ \operatorname{Prob}(X=3) & =\binom{4}{3}\left(\frac{1}{6}\right)^3\left(\frac{5}{6}\right)^1=\frac{5}{324} \\ \operatorname{Prob}(X=4) & =\binom{4}{4}\left(\frac{1}{6}\right)^4\left(\frac{5}{6}\right)^0=\frac{1}{1296} \end{aligned}

现在，可以求出 $X$ 的期望值：

E [X]=(-1) \cdot \frac{625}{1296}+1 \cdot \frac{125}{324}+2 \cdot \frac{25}{216}+3 \cdot \frac{5}{324}+4 \cdot \frac{1}{1296}=\frac{239}{1296}

由于期望值是正的，因此下注对我们是有利的。对上述情况的一种解释是，从平均水平看，在玩了 1296 次后，我们预计会有 239 美元的收入．