初学概率的人,遇到的第一个抽象概念就是密度函数和分布函数,对于初学者来讲,“概率密度”可能是最不友好的一个概念,直接谈概率不行吗,好好的为什么要搞出一个“密度函数”?的确,没有太多数理基础,这个概念着实不太好理解,我们先从两个引例来引入:
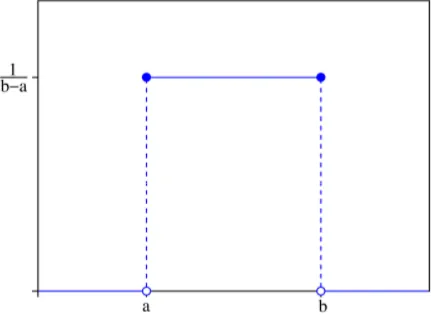
密度函数 Probability Density Function(PDF) 均匀分布的密度函数 均匀分布应该是比较容易理解的一种分布,比如数轴上有一段起点为a a a b b b ( b − a ) (b-a) ( b − a ) 1 b − a \frac{1}{b-a} b − a 1
p ( x ) = { 1 b − a , a < x < b , 0 , 其他. p(x)= \begin{cases}\frac{1}{b-a}, & a<x<b, \\ 0, & \text { 其他. }\end{cases} p ( x ) = { b − a 1 , 0 , a < x < b , 其他 . 既然是函数,我们就可以把初高中所学的那套知识拿来用了。既然是函数他就必须有定义域 和值域 ,显然定义域是a < x < b a<x<b a < x < b 1 b − a \frac{1}{b-a} b − a 1
这张图是一个常值的分段函数,因此,通过密度函数,就可以知道x x x 1 b − a \frac{1}{b-a} b − a 1
到这里,你也许能明白,数学是一个抽象的学科,他把现实世界对应的物理现象转换为了数学问题进行研究。 而密度函数 可以认为是概率问题和数学问题之间连接的桥梁。
正态分布的密度函数 不是每个函数的密度都很容易写出,比如正态分布的密度函数,我们在高中学过很多事物呈现正态分布,比如初中生的身高,很多都集中在 170 − 175 c m 170-175cm 170 − 175 c m 160 c m 160cm 160 c m 180 c m 180cm 180 c m
正态分布的概率密度函数的定义为:
φ ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , − ∞ < x < ∞ , \varphi(x)=\frac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2}}, \quad-\infty<x<\infty, φ ( x ) = 2 π σ 1 e − 2 σ 2 ( x − μ ) 2 , − ∞ < x < ∞ , 他是一条中间高、两边低的“钟形曲线”,这条曲线就是正态分布的概率密度曲线。通过概率密度曲线,可以很容易看出随机事件出现的概率趋势 ,比如从正态分布图可以看到中间的概率容易发生,两侧的概率发生率较低。
这里你也可以通过区间 的角度来理解概率密度曲线:曲线越高,也就代表着这个区间的概率越密集,简单理解成在同样大小的房子里,这个房间的人数更多、更挤。
总之,通过密度函数,我们把社会现实问题数学化,通过数学知识研究概率,这是高等数学和初等数学主要的区别。
离散型密度函数 离散型概率密度函数,其实不叫概率密度函数,离散型的就叫概率分别,一般也叫:分布列 或分布率 ,这个函数是用来求离散型随机变量,他通常使用列表求出。
例扔一枚质地均匀的硬币,正面、反面朝上的概率均为: 1 / 2 1 / 2 1/2
设:朝上的面为随机变量X X X X X X X X X = 0 , X =0, X = 0 , X = 1 =1 = 1 X X X X { 0 , 1 } X\{0,1\} X { 0 , 1 } ( X = (X= ( X = P ( X = 0 ) = 1 / 2 P(X=0)=1 / 2 P ( X = 0 ) = 1/2 ( X = (X= ( X = P ( X = 1 ) = 1 / 2 P(X=1)=1 / 2 P ( X = 1 ) = 1/2
连续性密度函数 连续型概率函数才叫:概率密度函数。为什么叫密度?由于连续型变量的取值是一个实数区间,如果把这个区间均分成多少份,则可无限细分下去 比如[0,1],如果按每段0.1,分成10段; 如果按每段0.01,则可分成100段; 如果按每段0.001,则可分成1000段;再往小了分,则每段越细,就像头发一样,越来越密,可以无限制的细分下去,于是叫密度函数
例 比如某公共汽车站从上午 7 时起, 每 15 分钟来一班车, 即 7:00、7:15、7:30、7:45等时刻有汽车到达此站, 如果乘客到达此站的时间 X X X
我们认为概率论很多概念比较难懂,就是因为他把离散型和连续型两种类型的研究糅合在了一起。事实上离散型和连续性本身研究方法有很大差别。
分布函数 Cumulative Distribution Function (CDF) 定义 :给一个随机变量 X X X x ∈ ( − ∞ , + ∞ ) x \in(-\infty,+\infty) x ∈ ( − ∞ , + ∞ ) F ( x ) = P ( X ≤ x ) F(x)=P(X \leq x) F ( x ) = P ( X ≤ x ) X X X
根据定义可以知道,对于a < b a<b a < b
P ( a < X ≤ b ) = P ( X ⩽ b ) − P ( X ⩽ a ) = F ( b ) − F ( a ) . . . ( 1 ) \boxed{
P(a<X \leq b)=P\left(X \leqslant b\right)-P\left(X \leqslant a\right)=F(b)-F(a) ...(1)
} P ( a < X ≤ b ) = P ( X ⩽ b ) − P ( X ⩽ a ) = F ( b ) − F ( a ) ... ( 1 ) 因此,若已知 X X X X X X ( a , b ] \left(a, b\right] ( a , b ]
如果将 X X X F ( x ) F(x) F ( x ) x x x X X X ( − ∞ , x ] (-\infty, x] ( − ∞ , x ]
由分布函数的定义可知,既然是函数,就要有定义域与值域。分布函数具有如下基本性质.
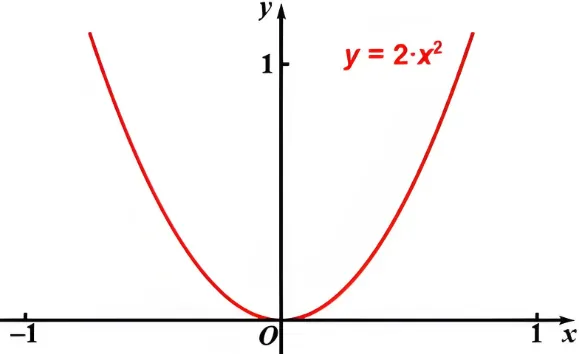
分布函数和传统的函数有什么不同? 分布函数和传统的函数在集合意义上有很大的不同。传统函数,比如y = x 2 y=x^2 y = x 2 x x x y y y y y y y y y
而分布函数的几何意义:在数轴上,将 X X X F ( x ) F(x) F ( x ) X X X X ⩽ x X \leqslant x X ⩽ x
请务必牢记分布函数的定义,他对离散型和连续性都成立。分布函数F ( X ) = P ( X ⩽ x ) F(X)=P(X \leqslant x) F ( X ) = P ( X ⩽ x ) F ( 90 ) = P ( X < 90 ) = 80 F(90)=P(X<90)=80 F ( 90 ) = P ( X < 90 ) = 80 F ( 60 ) = P ( X < 60 ) = 20 F(60)=P(X<60)=20 F ( 60 ) = P ( X < 60 ) = 20 60 − 90 60-90 60 − 90 F ( 90 ) − F ( 60 ) = 80 − 20 = 60 F(90)-F(60)=80-20=60 F ( 90 ) − F ( 60 ) = 80 − 20 = 60 ( a , b ) (a,b) ( a , b )
分布函数的性质 (1)单调性 F ( x ) F(x) F ( x ) ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) x 1 < x 2 x_1<x_2 x 1 < x 2 F ( x 1 ) ⩽ F ( x 2 ) F\left(x_1\right) \leqslant F\left(x_2\right) F ( x 1 ) ⩽ F ( x 2 ) (2)有界性 对任意的 x x x 0 ⩽ F ( x ) ⩽ 1 0 \leqslant F(x) \leqslant 1 0 ⩽ F ( x ) ⩽ 1
F ( − ∞ ) = lim x → − ∞ F ( x ) = 0 F ( + ∞ ) = lim x → + ∞ F ( x ) = 1 \begin{aligned}
& F(-\infty)=\lim _{x \rightarrow-\infty} F(x)=0 \\
& F(+\infty)=\lim _{x \rightarrow+\infty} F(x)=1
\end{aligned} F ( − ∞ ) = x → − ∞ lim F ( x ) = 0 F ( + ∞ ) = x → + ∞ lim F ( x ) = 1 几何解释:当区间端点 x x x ( x → − ∞ ) (x \rightarrow-\infty) ( x → − ∞ ) X X X x x x P ( X ⩽ x ) = F ( x ) P(X \leqslant x)=F(x) P ( X ⩽ x ) = F ( x ) x x x x → + ∞ x \rightarrow+\infty x → + ∞ X X X x x x P ( X ⩽ x ) = F ( x ) P(X \leqslant x)=F(x) P ( X ⩽ x ) = F ( x ) (3)右连续性 F ( x ) F(x) F ( x ) x x x x 0 x_0 x 0
lim x → x 0 + F ( x ) = F ( x 0 ) . \lim _{x \rightarrow x_0^{+}} F(x)=F\left(x_0\right) . x → x 0 + lim F ( x ) = F ( x 0 ) . 证略。
以上三条基本性质是分布函数必须具有的性质,反过来可以证明,任一满足这三个性质的函数, 一定可以作为某个随机变量的分布函数.
例通过某公交站牌的汽车每 10 min 一辆,随机变量 X X X
F ( x ) = { 0 , x < 0 x 10 , 0 ⩽ x < 10 1 , x ⩾ 10 F(x)= \begin{cases}0, & x<0 \\ \frac{x}{10}, & 0 \leqslant x<10 \\ 1, & x \geqslant 10\end{cases} F ( x ) = ⎩ ⎨ ⎧ 0 , 10 x , 1 , x < 0 0 ⩽ x < 10 x ⩾ 10 求:(1)P { X ⩽ 3 } P\{X \leqslant 3\} P { X ⩽ 3 } P { 1 < X ⩽ 9 } P\{1<X \leqslant 9\} P { 1 < X ⩽ 9 } P { X > 5 } P\{X>5\} P { X > 5 } P { X ⩽ 3 } = F ( 3 ) = 3 10 P\{X \leqslant 3\}=F(3)=\frac{3}{10} P { X ⩽ 3 } = F ( 3 ) = 10 3 P { 1 < X ⩽ 9 } = F ( 9 ) − F ( 1 ) = 4 5 P\{1<X \leqslant 9\}=F(9)-F(1)=\frac{4}{5} P { 1 < X ⩽ 9 } = F ( 9 ) − F ( 1 ) = 5 4 P { X > 5 } = 1 − F ( 5 ) = 1 − 1 2 = 1 2 P\{X>5\}=1-F(5)=1-\frac{1}{2}=\frac{1}{2} P { X > 5 } = 1 − F ( 5 ) = 1 − 2 1 = 2 1
例 设随机变量 X X X
F ( x ) = { a + b ( 1 + x ) 2 , x > 0 c , x ⩽ 0 F(x)= \begin{cases}a+\frac{b}{(1+x)^2}, & x>0 \\ c, & x \leqslant 0\end{cases} F ( x ) = { a + ( 1 + x ) 2 b , c , x > 0 x ⩽ 0 求常数 a , b , c a, b, c a , b , c F ( x ) F(x) F ( x ) 0 = F ( − ∞ ) = lim x → − ∞ F ( x ) = c 0=F(-\infty)=\lim _{x \rightarrow-\infty} F(x)=c 0 = F ( − ∞ ) = lim x → − ∞ F ( x ) = c c = 0 c=0 c = 0 1 = F ( + ∞ ) = lim x → + ∞ F ( x ) = lim x → + ∞ [ a + b ( 1 + x ) 2 ] = a 1=F(+\infty)=\lim _{x \rightarrow+\infty} F(x)=\lim _{x \rightarrow+\infty}\left[a+\frac{b}{(1+x)^2}\right]=a 1 = F ( + ∞ ) = lim x → + ∞ F ( x ) = lim x → + ∞ [ a + ( 1 + x ) 2 b ] = a a = 1 a=1 a = 1 F ( x ) F(x) F ( x ) lim x → 0 + F ( x ) = a + b = c \lim _{x \rightarrow 0^{+}} F(x)=a+b=c lim x → 0 + F ( x ) = a + b = c b = − 1 b=-1 b = − 1 a , b , c a, b, c a , b , c 1 , − 1 , 0 1,-1,0 1 , − 1 , 0
例 判别下列函数是否为某随机变量的分布函数.
(1) F ( x ) = { 0 , x < − 2 1 2 , − 2 ⩽ x < 0 ; 1 , x ⩾ 0 F(x)=\left\{\begin{array}{ll}0, & x<-2 \\ \frac{1}{2}, & -2 \leqslant x<0 \text { ; } \\ 1, & x \geqslant 0\end{array}\right. F ( x ) = ⎩ ⎨ ⎧ 0 , 2 1 , 1 , x < − 2 − 2 ⩽ x < 0 ; x ⩾ 0 F ( x ) = { 0 , x < 0 sin x , 0 ⩽ x < π 1 , x ⩾ π F(x)=\left\{\begin{array}{ll}0, & x<0 \\ \sin x, & 0 \leqslant x<\pi \\ 1, & x \geqslant \pi\end{array}\right. F ( x ) = ⎩ ⎨ ⎧ 0 , sin x , 1 , x < 0 0 ⩽ x < π x ⩾ π F ( x ) = { 0 , x < 0 x + 1 2 , 0 ⩽ x < 1 2 1 , x ⩾ 1 2 F(x)=\left\{\begin{array}{ll}0, & x<0 \\ x+\frac{1}{2}, & 0 \leqslant x<\frac{1}{2} \\ 1, & x \geqslant \frac{1}{2}\end{array}\right. F ( x ) = ⎩ ⎨ ⎧ 0 , x + 2 1 , 1 , x < 0 0 ⩽ x < 2 1 x ⩾ 2 1
解 (1) 由题设, F ( x ) F(x) F ( x ) ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ )
F ( − ∞ ) = lim x → − ∞ F ( x ) = 0 , F ( + ∞ ) = lim x → + ∞ F ( x ) = 1 , F(-\infty)=\lim _{x \rightarrow-\infty} F(x)=0, \quad F(+\infty)=\lim _{x \rightarrow+\infty} F(x)=1, F ( − ∞ ) = x → − ∞ lim F ( x ) = 0 , F ( + ∞ ) = x → + ∞ lim F ( x ) = 1 , 所以 F ( x ) F(x) F ( x ) X X X F ( x ) F(x) F ( x ) ( π 2 , π ) \left(\frac{\pi}{2}, \pi\right) ( 2 π , π ) F ( x ) F(x) F ( x ) F ( x ) F(x) F ( x ) ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ )
F ( − ∞ ) = lim x → − ∞ F ( x ) = 0 , F ( + ∞ ) = lim x → + ∞ F ( x ) = 1 , F(-\infty)=\lim _{x \rightarrow-\infty} F(x)=0, \quad F(+\infty)=\lim _{x \rightarrow+\infty} F(x)=1, F ( − ∞ ) = x → − ∞ lim F ( x ) = 0 , F ( + ∞ ) = x → + ∞ lim F ( x ) = 1 , 所以 F ( x ) F(x) F ( x ) X X X
上面主要讨论了随机变量的概念及分布函数, 利用随机变量可以描述和研究随机现象,而利用分布函数能很好地表示各事件的概率. 并且可以推导下面几个有用的公式
P { X > a } = 1 − P { X ⩽ a } = 1 − F ( a ) , P { X < a } = F ( a − 0 ) , P { X = a } = F ( a ) − F ( a − 0 ) . . . . ( 2 ) \boxed{
\begin{aligned}
& P\{X>a\}=1-P\{X \leqslant a\}=1-F(a), \\
& P\{X<a\}=F(a-0), \\
& P\{X=a\}=F(a)-F(a-0) .
\end{aligned} ...(2)
} P { X > a } = 1 − P { X ⩽ a } = 1 − F ( a ) , P { X < a } = F ( a − 0 ) , P { X = a } = F ( a ) − F ( a − 0 ) . ... ( 2 ) 在引进了随机变量和分布函数后,就能利用高等数学的许多结果和方法来研究各种随机现象, 它们是概率论的两个重要而基本的概念.
请注意:分布函数的定义对离散型和连续型都适用。
理解:再论为啥引入分布函数 既然有概率密度了,为啥还要搞一个分布函数?答案是方便计算概率。
这里请务必牢记,分布函数是一个累加值,例如有一个分布函数 F ( 90 ) = 80 F(90)=80 F ( 90 ) = 80 X X X F ( 60 ) = 20 F(60)=20 F ( 60 ) = 20 X X X P ( 60 ≤ X ≤ 90 ) = F ( 90 ) − F ( 60 ) P(60 \le X \le 90)=F(90)-F(60) P ( 60 ≤ X ≤ 90 ) = F ( 90 ) − F ( 60 )
上面举的是离散型的例子,很容易理解,但是对于连续型的呢?这里有一个重要的结论:密度函数的积分(面积)等于概率 ,概率密度函数和分布函数的的一个重要关系就是,
分布函数求导是密度函数,密度函数积分是分别函数 。
随机变量X X X ( a , b ) (a,b) ( a , b ) a < X < b a < X < b a < X < b ( a , b ) (a,b) ( a , b )
下图中的三条曲线f ( x ) f(x) f ( x )
概率密度函数图像
分布函数图像和密度函数图像 图2.2(a), (b)分别表示某一连续型变量 X X X F F F f f f μ \mu μ X X X a , b a, b a , b
通常认为,分布函数的图像意义并不大,通过分布函数图像并不能得出有效的结论,分布函数主要用来求密度函数,一般都使用密度函数的图像了解概率分布规律。
分布函数例题 例口袋里装有 3 个白球和 2 个红球, 从中任取三个球, 求取出的三个球中的白球数的分布函数.
解 设 X X X X X X 1 、 2 、 3 1 、 2 、 3 1 、 2 、 3
P ( X = 1 ) = C 2 2 C 3 1 C 5 3 = 0.3 ; P ( X = 2 ) = C 2 1 C 3 2 C 5 3 = 0.6 P ( X = 3 ) = C 3 3 C 5 3 = 0.1 \begin{gathered}
P(X=1)=\frac{C_2^2 C_3^1}{C_5^3}=0.3 ; \\
P(X=2)=\frac{C_2^1 C_3^2}{C_5^3}=0.6 \\
P(X=3)=\frac{C_3^3}{C_5^3}=0.1
\end{gathered} P ( X = 1 ) = C 5 3 C 2 2 C 3 1 = 0.3 ; P ( X = 2 ) = C 5 3 C 2 1 C 3 2 = 0.6 P ( X = 3 ) = C 5 3 C 3 3 = 0.1 当 x < 1 x<1 x < 1 { X ⩽ x } \{X \leqslant x\} { X ⩽ x }
F ( x ) = P { X ⩽ x } = 0 ; F(x)=P\{X \leqslant x\}=0 ; F ( x ) = P { X ⩽ x } = 0 ; 当 1 ⩽ x < 2 1 \leqslant x<2 1 ⩽ x < 2 { X ⩽ x } = { X = 1 } \{X \leqslant x\}=\{X=1\} { X ⩽ x } = { X = 1 }
F ( x ) = P { X ⩽ x } = P { X = 1 } = 0.3 ; F(x)=P\{X \leqslant x\}=P\{X=1\}=0.3 ; F ( x ) = P { X ⩽ x } = P { X = 1 } = 0.3 ; 当 2 ⩽ x < 3 2 \leqslant x<3 2 ⩽ x < 3 { X ⩽ x } = { X = 1 } ⋃ { X = 2 } \{X \leqslant x\}=\{X=1\} \bigcup\{X=2\} { X ⩽ x } = { X = 1 } ⋃ { X = 2 } { X = 1 } ∩ { X = 2 } = ∅ \{X=1\} \cap\{X=2\}=\varnothing { X = 1 } ∩ { X = 2 } = ∅
F ( x ) = P { X ⩽ x } = P { X = 1 } + P { X = 2 } = 0.9 F(x)=P\{X \leqslant x\}=P\{X=1\}+P\{X=2\}=0.9 F ( x ) = P { X ⩽ x } = P { X = 1 } + P { X = 2 } = 0.9 当 x ⩾ 3 x \geqslant 3 x ⩾ 3 { X ⩽ x } \{X \leqslant x\} { X ⩽ x }
综上所述, X X X
F ( x ) = { 0 x < 1 0.3 1 ⩽ x < 2 0.9 2 ⩽ x < 3 1 x ⩾ 3 . F(x)=\left\{\begin{array}{ll}
0 & x<1 \\
0.3 & 1 \leqslant x<2 \\
0.9 & 2 \leqslant x<3 \\
1 & x \geqslant 3
\end{array} .\right. F ( x ) = ⎩ ⎨ ⎧ 0 0.3 0.9 1 x < 1 1 ⩽ x < 2 2 ⩽ x < 3 x ⩾ 3 . 例设随机变量 X X X X X X P { X ⩽ 1 2 } , P { 3 2 < X ⩽ 5 2 } , P { 2 ⩽ X ⩽ 3 } P\left\{X \leqslant \frac{1}{2}\right\}, P\left\{\frac{3}{2}<X \leqslant \frac{5}{2}\right\}, P\{2 \leqslant X \leqslant 3\} P { X ⩽ 2 1 } , P { 2 3 < X ⩽ 2 5 } , P { 2 ⩽ X ⩽ 3 }
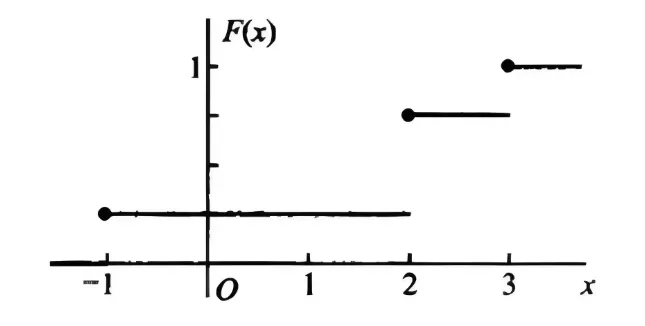
解 X X X x = − 1 , 2 , 3 x=-1,2,3 x = − 1 , 2 , 3 ≠ 0 \neq 0 = 0 F ( x ) F(x) F ( x ) X ⩽ x X \leqslant x X ⩽ x x x x x k x_k x k p k p_k p k
F ( x ) = { 0 x < − 1 , P { X = − 1 } , − 1 ⩽ x < 2 , P { X = − 1 } + P { X = 2 } , 2 ⩽ x < 3 , 1 , x ⩾ 3. F(x)= \begin{cases}0 & x<-1, \\ P\{X=-1\}, & -1 \leqslant x<2, \\ P\{X=-1\}+P\{X=2\}, & 2 \leqslant x<3, \\ 1, & x \geqslant 3 .\end{cases} F ( x ) = ⎩ ⎨ ⎧ 0 P { X = − 1 } , P { X = − 1 } + P { X = 2 } , 1 , x < − 1 , − 1 ⩽ x < 2 , 2 ⩽ x < 3 , x ⩾ 3. 即
F ( x ) = { 0 , x < − 1 , 1 4 , − 1 ⩽ x < 2 , 3 4 , 2 ⩽ x < 3 , 1 , x ⩾ 3. F(x)=\left\{\begin{array}{l}
0, x<-1, \\
\frac{1}{4},-1 \leqslant x<2, \\
\frac{3}{4}, 2 \leqslant x<3, \\
1, x \geqslant 3 .
\end{array}\right. F ( x ) = ⎩ ⎨ ⎧ 0 , x < − 1 , 4 1 , − 1 ⩽ x < 2 , 4 3 , 2 ⩽ x < 3 , 1 , x ⩾ 3. F ( x ) F(x) F ( x ) x = − 1 , 2 , 3 x=-1,2,3 x = − 1 , 2 , 3 1 4 , 1 2 , 1 4 \frac{1}{4}, \frac{1}{2}, \frac{1}{4} 4 1 , 2 1 , 4 1
P { X ⩽ 1 2 } = F ( 1 2 ) = 1 4 , P\left\{X \leqslant \frac{1}{2}\right\}=F\left(\frac{1}{2}\right)=\frac{1}{4}, P { X ⩽ 2 1 } = F ( 2 1 ) = 4 1 , P { 3 2 < X ⩽ 5 2 } = F ( 5 2 ) − F ( 3 2 ) = 3 4 − 1 4 = 1 2 . P\left\{\frac{3}{2}<X \leqslant \frac{5}{2}\right\}=F\left(\frac{5}{2}\right)-F\left(\frac{3}{2}\right)=\frac{3}{4}-\frac{1}{4}=\frac{1}{2} . P { 2 3 < X ⩽ 2 5 } = F ( 2 5 ) − F ( 2 3 ) = 4 3 − 4 1 = 2 1 . P { 2 ⩽ X ⩽ 3 } = F ( 3 ) − F ( 2 ) + P { X = 2 } = 1 − 3 4 + 1 2 = 3 4 . P\{2 \leqslant X \leqslant 3\} =F(3)-F(2)+P\{X=2\} =1-\frac{3}{4}+\frac{1}{2}=\frac{3}{4} . P { 2 ⩽ X ⩽ 3 } = F ( 3 ) − F ( 2 ) + P { X = 2 } = 1 − 4 3 + 2 1 = 4 3 . 例在数轴上的有界区间 [ a , b ] [a, b] [ a , b ] X X X X X X
解 当 x < a x<a x < a { X ⩽ x } \{X \leqslant x\} { X ⩽ x } F ( x ) = P { X ⩽ x } = 0 F(x)=P\{X \leqslant x\}=0 F ( x ) = P { X ⩽ x } = 0 a ⩽ x < b a \leqslant x<b a ⩽ x < b { X ⩽ x } = { a ⩽ X ⩽ x } \{X \leqslant x\}=\{a \leqslant X \leqslant x\} { X ⩽ x } = { a ⩽ X ⩽ x } [ a , x ] ⊂ [ a , b ] [a, x] \subset[a, b] [ a , x ] ⊂ [ a , b ]
F ( x ) = P { X ⩽ x } = P { a ⩽ X ⩽ x } = x − a b − a ; F(x)=P\{X \leqslant x\}=P\{a \leqslant X \leqslant x\}=\frac{x-a}{b-a} ; F ( x ) = P { X ⩽ x } = P { a ⩽ X ⩽ x } = b − a x − a ; 当 x ⩾ b x \geqslant b x ⩾ b { X ⩽ x } = { a ⩽ X ⩽ b } \{X \leqslant x\}=\{a \leqslant X \leqslant b\} { X ⩽ x } = { a ⩽ X ⩽ b }
F ( x ) = P { X ⩽ x } = P { a ⩽ X ⩽ b } = b − a b − a = 1. F(x)=P\{X \leqslant x\}=P\{a \leqslant X \leqslant b\}=\frac{b-a}{b-a}=1 . F ( x ) = P { X ⩽ x } = P { a ⩽ X ⩽ b } = b − a b − a = 1. 综上可得, X X X F ( x ) = { 0 , x < a x − a b − a , a ⩽ x < b 1 , x ⩾ b F(x)=\left\{\begin{array}{cc}0, & x<a \\ \frac{x-a}{b-a}, & a \leqslant x<b \\ 1, & x \geqslant b\end{array}\right. F ( x ) = ⎩ ⎨ ⎧ 0 , b − a x − a , 1 , x < a a ⩽ x < b x ⩾ b
 {width=300px}
{width=300px}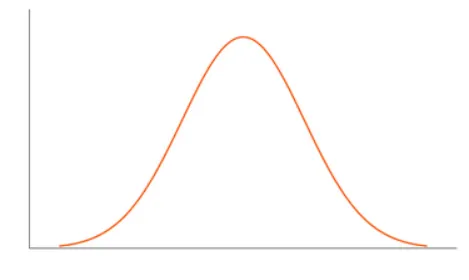 {width=300px}
{width=300px}
 {width=300px}
{width=300px}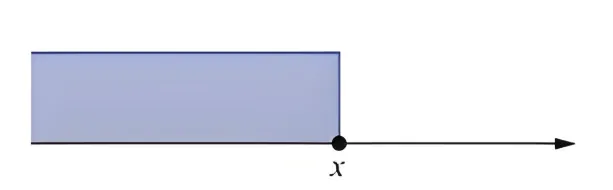 {width=300px}
{width=300px}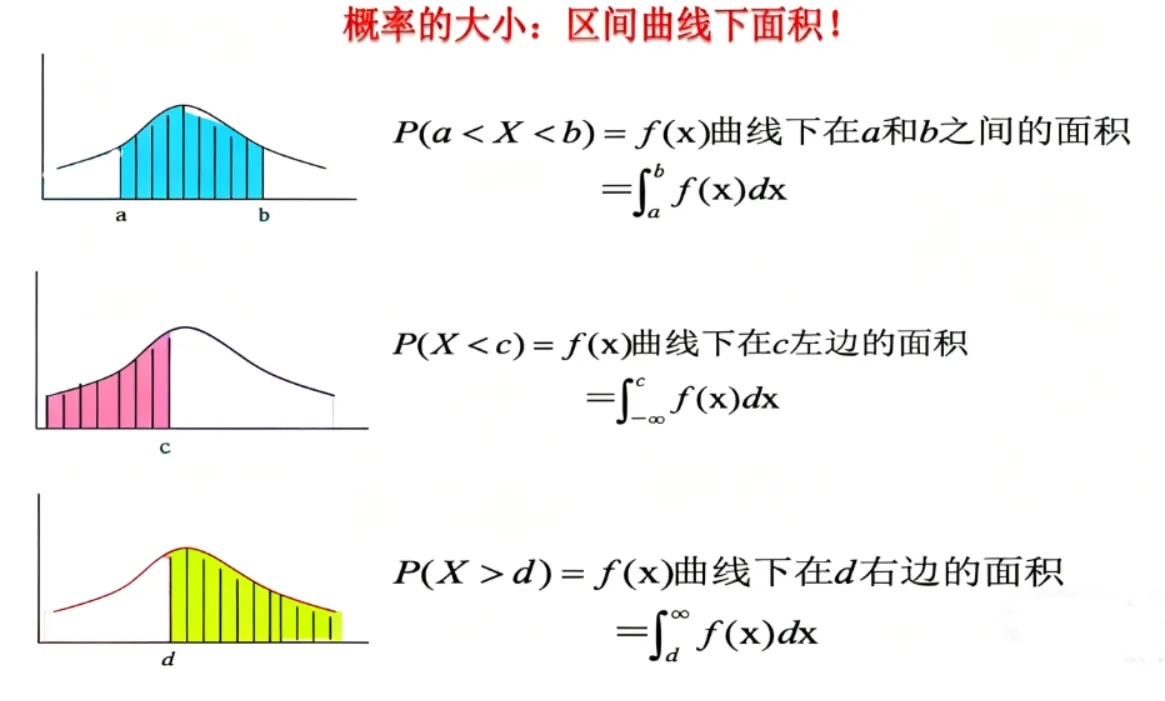 概率密度函数图像
概率密度函数图像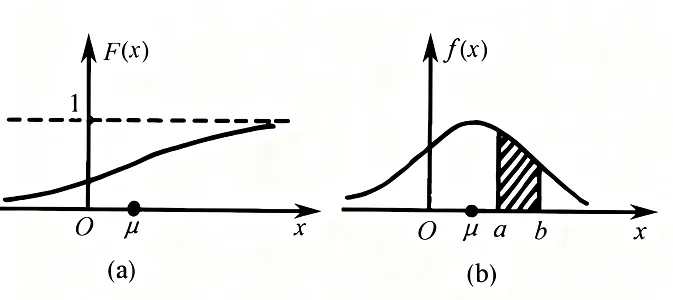
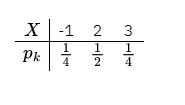 求 的分布函数, 并求 .
求 的分布函数, 并求 .