标准正态分布
称 μ=0,σ=1 时的正态分布 N(0,1) 为标准正态分布.也称为高斯分布。
标准正态分布的密度函数为 φ(u),其图像如下
φ(x)=2π1e−2x2,−∞<x<∞, 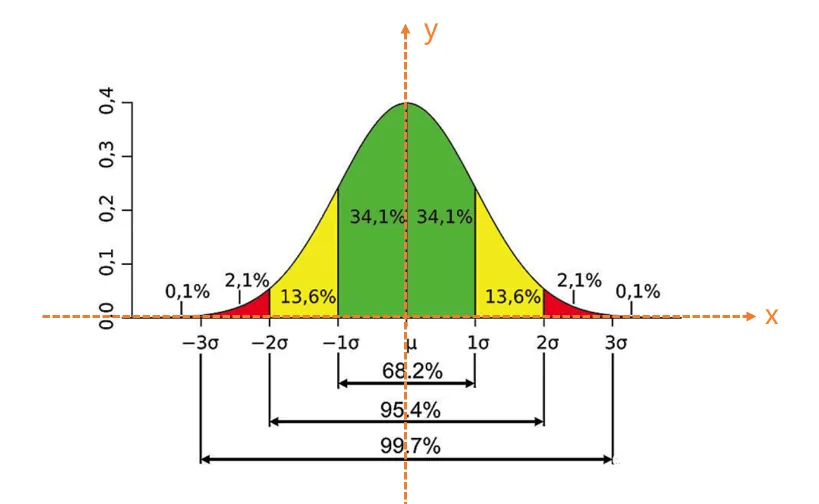 {width=600px}
{width=600px}
从标准正态分布的密度函数可以看到:
(1)因为密度函数是偶函数,所以函数图像关于y轴对称
(2)密度函数定义域为(−∞,+∞) 在−3σ−3σ之间占据了几乎所有面积,所以,−3σ−3σ 被称为 3σ 原则
分布函数
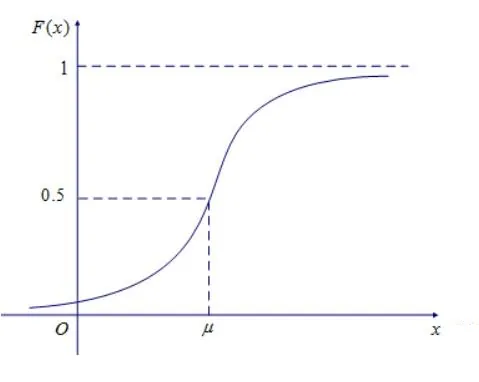
正态分布的分布函数 Φ(u)
Φ(x)=2π1∫−∞xe−2t2 dt,−∞<x<∞. 这个函数是积不出来的,所以只能使用积分符号写着。他的函数图像如下: 函数在 x=u 时取到0.5.
 {width=300px}
{width=300px}
由于标准正态分布的分布函数不含任何未知参数, 故其值 Φ(X)=P(X⩽x) 完全可以算出,
性质1 当 x>0 时, Φ(x) 的值可以查概率函数值表得到,且P(a<X≤b)=Φ(b)−Φ(a)
性质2 当 x<0 时,由密度函数对称性可得 Φ(x)=1−Φ(−x) ,特别地,有 Φ(0)=21 ;
性质3 若 X∼N(μ,σ2) ,则 P(a<X≤b)=Φ(σb−μ)−Φ(σa−μ)特别地 P(X≤b)=Φ(σb−μ)P(X>a)=1−Φ(σa−μ)
这些等式都不难推得.
这里请务必牢记,分布函数是一个累加值,例如 Φ(90)=80 表示分数X小于90分的有80人,Φ(60)=20表示分数X小于60分的有20人,现在要求分数介于60~90分之间的人数,其计算方法就是P(60≤X≤90)=Φ(90)−Φ(60), 这就是上面性质1的意思。
如何理解正态分布的密度函数
假设某校的初中生身高服从 X∼N(170,62)(单位cm)的正态分布,这里的μ 相当于平均身高,σ相当于身高误差。这句话转换为通俗语言就是:某城市初中生平均身高在170cm,其中大部分身高分布在164cm−176cm。
因为正态分布是连续性分布,总概率为1,这意味问某一点身高的概率始终为零,身高从 −∞ 到 +∞ 的总概率为1.
从数学计算可以的都如下结论
P(μ−σ<X<μ+σ)=2Φ(1)−1=0.6826,P(μ−2σ<X<μ+2σ)=2Φ(2)−1=0.9545,P(μ−3σ<X<μ+3σ)=2Φ(3)−1=0.9973. 第一个等式表明,身高在 164cm−176cm 的占比 68.26%
第二个等式表明,身高在 158cm−182cm 的占比 95.45%
第三个等式表明,身高在 152cm−188cm 的占比 99.73%
标准正态分布的数学期望与方差
正态分布的数学期望E(X)=0, 方差为D(X)=1
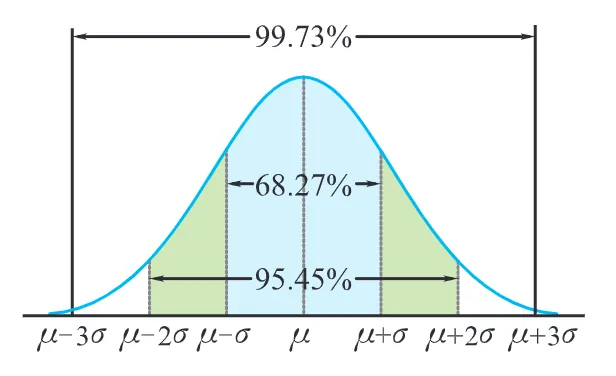
正态分布的 3σ 原则
若 X∼N(μ,σ2), 则随机变量 X 在 μ 的附近取值的概率较大, 在离 μ 较远处取值的概率较小.
设随机变量 X∼N(μ,σ2), 则
P(μ−kσ<X<μ+kσ)=P(σX−μ<k)=Φ(k)−Φ(−k)=2Φ(k)−1 当 k=1,2,3 时,有
P(μ−σ<X<μ+σ)=2Φ(1)−1=0.6826,P(μ−2σ<X<μ+2σ)=2Φ(2)−1=0.9545,P(μ−3σ<X<μ+3σ)=2Φ(3)−1=0.9973. 具体地, 如图所示, 随机变量 X 取值
落在区间 (μ−σ,μ+σ) 内的概率约为 68.27% ,
落在区间 (μ−2σ,μ+2σ) 内的概率约为 95.45%,
落在区间 (μ−3σ,μ+3σ) 内的概率约为 99.73%.
 {width=380px}
{width=380px}
这是正态分布的重要性质被称为正态分布的 3σ 原则.
假如某随机变量取值的概率近似满足上面的值, 则可认为这个随机变量近似服从正态分布; 假如三式中有一个偏差较大, 则可以认为这个随机变量不服从正态分布. 这就是正态分布的 3σ 原则, 这个原则在 X 的观察值较多 (成百上千个) 时, 常用于判断 X 的分布是否近似服从正态分布.
在生产中某产品的质量要求常规定其上、下控制限, 若上、下控制限能覆盖区间 (μ−3σ,μ+3σ), 则称该生产过程受控制, 并称其比值
Cp=6σ 上控制限一下控制限 为过程能力指数. 当 Cp<1 时, 认为生产过程不足; 当 Cp⩾1.33 时, 认为生产过程正常;当 Cp 为其他值时, 常认为生产过程不稳定, 需要改进.
一般地,有下列结论:
设随机变量 X∼N(0,1),c>0 则
P(∣X∣<c)=Φ(c)−Φ(−c)=2Φ(c)−1P(∣X∣>c)=1−P(∣X∣≤c)=2−2Φ(c) 若 X∼N(μ,σ2) ,则
P(a<X≤c)=Φ(σb−μ)−Φ(σa−μ) 特别地 P(X≤b)=Φ(σb−μ);P(X>a)=1−Φ(σa−μ)
关于上面的结论,请点击 此处 理解
例设 X∼N(0,4) ,试求概率 P(X≤3),P(X≤−3)
解 查表并计算可得
P(X≤3)=Φ(23−1)=Φ(1)=0.8413 P(X≤−3)=Φ(2−3−1)=1−Φ(2)=0.0228 例设随机变量 X 服从标准正态分布 N(0,1),c 为何值时才能满足
P(X≤c)=0.95 解 由 P(X≤c)=Φ(c)=0.95 ,查附录 知
Φ(1.645)=0.95⇒c=1.645 典型例题
例 设随机变量 X 服从正态分布 N(108,32), 试求:
(1) P(102<X<117);
(2) 常数 a, 使得 P(X<a)=0.95.
解:由题意知μ=108,σ=3, 利用上面公式及下面附表得
(1)
P(102<X<117)=Φ(3117−108)−Φ(3102−108)=Φ(3)−Φ(−2)=Φ(3)+Φ(2)−1=0.9987+0.9772−1=0.9759. 上面计算利用了 F(−x)=1−F(x) 这个性质。
(2) 由
P(X<a)=Φ(3a−108)=0.95, 或 Φ−1(0.95)=3a−108, 其中 Φ−1 为 Φ 的反函数. 从附表由里向外反查得
Φ(1.64)=0.9495,Φ(1.65)=0.9505, 再用线性内插法可得 Φ(1.645)=0.95, 即 Φ−1(0.95)=1.645, 故
3a−108=1.645, 从中解得 a=112.935.
从上例我们可以看出, 有些场合下给定 Φ(x) 的值 p, 可以从附表 2 中由里向外反查表来得到 xp, 使 Φ(xp)=p 或 Φ−1(p)=xp, 这时 xp 称为标准正态分布的 p 分位数. 在上例中就是标准正态分布的 0.95 分位数, 更一般叙述见分位数在统计中被大量使用.
例 在考试中, 如果考生的成绩 X 近似地服从正态分布, 则通常认为这次考试(就合理地划分考生成绩的等级而言)是正常的。教师经常把分数超过 μ+σ 的评为 A等, 分数在 μ 到 μ+σ 之间的评为 B 等, 分数在 μ−σ 到 μ 之间的评为 C 等, 分数在 μ−2σ到 μ−σ 之间的评为 D 等, 分数在 μ−2σ 以下的评为 F 等. 由此可计算得:
P(X⩾μ+σ)=P(σX−μ⩾1)=1−Φ(1)≈0.1587,P(μ⩽X<μ+σ)=P(0⩽σX−μ<1)=Φ(1)−Φ(0)≈0.3413,P(μ−σ⩽X<μ)=P(−1⩽σX−μ<0)=Φ(0)−Φ(−1)≈0.3413,P(μ−2σ⩽X<μ−σ)=P(−2⩽σX−μ<−1)=Φ(−1)−Φ(−2)≈0.1359,P(X<μ−2σ)=P(σX−μ<−2)=Φ(−2)≈0.0228. 这说明:用这种方法划分成绩的等级,获得 A 等的约占 16%,B 等的约占 34%,C 等的约占 34%,D 等的约占 14%,F 等的约占 2%.
 {width=600px}
{width=600px} {width=300px}
{width=300px} {width=380px}
{width=380px}