10._p值和_p值检验法

p值和 p值检验法

前面讨论的假设检验方法是根据统计值是否落入拒绝域来做出判断的，该方法称为临界值法。在实际应用中还有另一种检验方法— $p$ 值检验法。下面以正态总体关于 $\mu$ 的单侧检验为例进行说明。

设总体 $X \sim N\left(\mu, \sigma^2\right), X_1, X_2, \cdots, X_n$ 是取自总体 $X$ 的一个样本，给定显著性水平为 $\alpha(0<\alpha<1)$ ，若 $\sigma^2$ 已知，检验假设

选取检验统计量为 $U=\frac{\bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)$ ，由样本观测值求出 $U$ 的观测值 $u_0$ 。

若使用临界值法，则当 $u_0$ 落入拒绝域 $U>u_\alpha$ 时，应拒绝 $H_0$ ；当 $u_0$ 不落入拒绝域 $U>u_\alpha$ 时，应接受 $H_0$ 。

若换一个思路，求出一个特殊概率

如图所示。

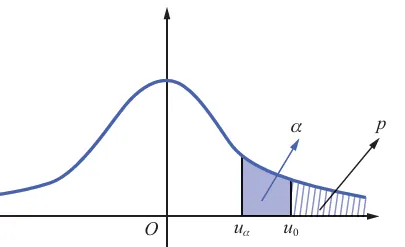
当 $p \leqslant \alpha$ 时，表示观测值 $u_0$ 落在拒绝域内，因而拒绝 $H_0$ 。

当 $p>\alpha$ 时，表示观测值 $u_0$ 不落在拒绝域内，因而接受 $H_0$ ．

由此可得p值的定义及p值检验法如下．

定义 假设检验问题的 $p$ 值（Probability Value）是由检验统计量的样本观测值得出的原假设可被拒绝的最小显著性水平。

按照 $p$ 值的定义，对于任意指定的显著性水平 $\alpha$ ，有以下结论。 （1）当 $p \leqslant \alpha$ 时，在显著性水平 $\alpha$ 下拒绝 $H_0$ 。 （2）当 $p>\alpha$ 时，在显著性水平 $\alpha$ 下接受 $H_0$ 。 这种利用 $p$ 值进行检验的方法，称为 $p$ 值检验法．

例设某种特殊类型的集成电路所用硅晶圆片的目标厚度为 $245 \mu \mathrm{~m}$ ，在正常情况下，产品厚度应该服从正态分布 $N\left(245,3.6^2\right)$ ．我们抽取了 50 个硅晶圆片样品，并测定了每个硅晶圆片的厚度，得到了样品的平均厚度为 $246.18 \mu \mathrm{~m}$ ，这些数据是否表明实际的硅晶圆片平均厚度与目标值有显著差异呢？(用P值检验法)

解 本例要检验的是实际的硅晶圆片平均厚度与目标厚度 245 （单位：$\mu \mathrm{m}$ ）是否有显著差异，故建立假设

选取 $U=\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}$ 为检验统计量，当 $H_0$ 成立时，

计算统计量 $U$ 的观测值为 $u_0=\frac{246.18-245}{\frac{3.6}{\sqrt{50}}}=2.32$ ． 根据 $u_0$ 求出 $p$ 值，因为本题是双侧检验，故

若本例中显著性水平 $\alpha=0.05$ ，则 $p \leqslant \alpha$ ，从而拒绝 $H_0$ ，即认为实际的硅晶圆片平均厚度与目标值有显著差异．

若本例中显著性水平 $\alpha=0.01$ ，则 $p>\alpha$ ，从而接受 $H_0$ ，即认为实际的硅晶圆片平均厚度与目标值没有显著差异．

由上述例题可以看出，用临界值法进行检验时，对于每一个不同的显著性水平 $\alpha$ ，都要确定不同的拒绝域．而 $p$ 值检验法的优点在于：只要得到了 $p$ 值，对于每一个不同的显著性水平 $\alpha$ ，都可以经过比较，直接做出判断．

既然p值检验法有优势，那么p值该如何得到呢？ 任一检验问题的p值可以根据检验统计量的分布及观测值求出，但过程往往较为复杂．在现代计算机统计软件中，一般直接给出检验问题的p值．

例一美国汽车厂商声称他们生产的某节能型汽车耗油量低于 29 (单位: 英里/加仑, 简称 mpg ), 另一汽车厂商表示怀疑，他抽取了一组同是这一型号的不同汽车的行驶记录共 16 条, 得到平均耗油量观测值为 28 , 假设该节能型汽车的耗油量 $X \sim N(\mu, 9)$ ，请问在显著性水平 $\alpha=0.05$假定下，能否接受耗油量低于 29 的假设；若显著性水平为 $\alpha=0.1$, 则结论会有变化吗?

解 建立假设 $H_0: \mu \geqslant 29 \leftrightarrow H_1: \mu<29$, 给出未知参数 $\mu$ 的估计 $\hat{\mu}=\bar{x}=28$, 则

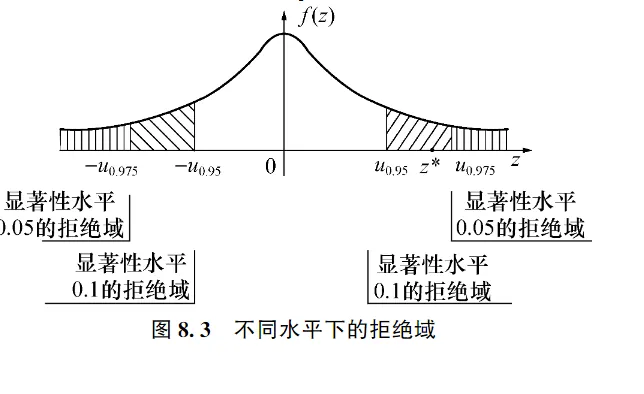
当显著性水平 $\alpha=0.05$ 时， $0.0918>0.05$ ，故不能拒绝 $H_0$ ，认为耗油量不低于 29 mpg 。当显著性水平 $\alpha=0.1$ 时， $0.0918<0.1$ ，故拒绝 $H_0$ ，认为耗油量低于 29 mpg 。 这个例子告诉我们，在一个较小的显著性水平 $(\alpha=0.05)$ 下得到不能拒绝原假设 $H_0$的结论，而在一个较大的显著性水平（ $\alpha=0.1$ ）下，同一组样本数据却得到了相反的结论。原因在于，当显著性水平变大时，会导致检验的拒绝域变大，原本落在接受域内的数据可能落到拒绝域内，因而更容易拒绝 $H_0$ (如图8.3 所示). 这就给实际工作带来一定的麻烦，可能同一个问题，在不同的显著性水平假定下得到不同的结论，换一个角度，给出 $p$ 值，由使用者自己决策以多大的显著性水平来拒绝原假设。所以，在实际应用中，当我们进行假设检验时，更常见的是给出 $p$ 值，因为 $p$ 值比拒绝域提供更多信息, 使用也更灵活.

从上述例题可以看出，用临界值法进行检验时，对于每一个不同的显著性水平α，都要确 定不同的拒绝域．而p值检验法的优点在于：只要得到了p值，对于每一个不同的显著性水平 α，都可以经过比较，直接做出判断． 既然p值检验法有优势，那么p值该如何得到呢？ 任一检验问题的p值可以根据检验统计量的分布及观测值求出，但过程往往较为复杂．在 现代计算机统计软件中，一般直接给出检验问题的p值．