5._两个正态总体均均值的假设检验_Z检验与t检验

在实际应用当中，我们还常常会遇到两个正态总体的参数比较问题，例如，比较两个品牌的同排量汽车的平均耗油量的优劣；又如，比较两台仪器测量精度的高低，等等．这些问题都可以在单个正态总体参数检验的基础上加以推广。

两个都是正态分布，通常有3种检验类型

(1)$\sigma_1^2, \sigma_2^2$ 已知，关于均值差 $\mu_1-\mu_2$ 的检验 (2)$\sigma_1^2, \sigma_2^2$ 末知，但 $\sigma_1^2=\sigma_2^2$ ，关于均值差 $\mu_1-\mu_2$ 的检验 (3) $\mu_1, \mu_2$ 未知，关于方差比 $\frac{\sigma_1^2}{\sigma_2^2}$ 的检验

本节介绍(1)(2)检验法，下一节介绍(3) 检验法

两个正态总体均值的假设检验

设 $X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right), X_1, X_2, \cdots, X_{n_1}$ 为取自总体 $X$ 的一个样本，$Y_1, Y_2, \cdots, Y_{n_2}$ 为取自总体 $Y$ 的一个样本，记 $\bar{X}$ 与 $\bar{Y}$ 分别为样本 $X_1, X_2, \cdots, X_{n_1}$ 与 $Y_1, Y_2, \cdots, Y_{n_2}$ 的均值，并且两个样本相互独立．关于正态均值 $\mu_1$ 和 $\mu_2$ 的比较，有如下三种检验问题： （1）$H_0: \mu_1=\mu_2, H_1: \mu_1 \neq \mu_2$ （2）$H_0: \mu_1 \leqslant \mu_2, H_1: \mu_1>\mu_2$ （3）$H_0: \mu_1 \geqslant \mu_2, H_1: \mu_1<\mu_2$ 等价形式分别为 （1）$H_0: \mu_1-\mu_2=0, H_1: \mu_1-\mu_2 \neq 0$ （2）$H_0: \mu_1-\mu_2 \leqslant 0, H_1: \mu_1-\mu_2>0$ （3）$H_0: \mu_1-\mu_2 \geqslant 0, H_1: \mu_1-\mu_2<0$

1．方差 $\sigma_1^2, ~ \sigma_2^2$ 已知，关于数学期望的假设检验（ $Z$ 检验法）

首先考虑双边假设检验。 （1）检验假设

由 $\bar{X}$ 与 $\bar{Y}$ 分别为总体 $X$ 和总体 $Y$ 的样本均值及第 6 章的知识可知

由两样本独立及期望和方差的性质可得

故随机变量 $\bar{X}-\bar{Y}$ 也服从正态分布，即

从而

采用 $Z$ 检验方法，选取 $Z$ 统计量为

当 $H_0$ 为真时

由于 $\bar{X}$ 与 $\bar{Y}$ 分别是 $\mu_1$ 与 $\mu_2$ 的无偏估计量，当 $H_0$ 为真时， $\bar{x}$ 与 $\bar{y}$ 应较为接近，不应太大，若 $\bar{x}$ 距离 $\bar{y}$ 较远时，应拒绝 $H_0$ 。类似前面的讨论可得此检验问题的拒绝域形式为

对于给定的显著性水平 $\alpha$ ，有

由此即得拒绝域为

根据一次抽样后得到的样本观察值 $x_1, x_2, \cdots, x_{n_1}$ 和 $y_1, y_2, \cdots, y_{n_2}$ 计算出 $Z$ 的观察值 $z$ ，若 $|z| \geqslant z_{\alpha / 2}$ ，则拒绝原假设 $H_0$ ，即认为总体均值 $\mu_1$ 与 $\mu_2$ 有显著差异；若 $|z|<z_{\alpha / 2}$ ，则接受原假设 $H_0$ ，即认为总体均值 $\mu_1$ 与 $\mu_2$ 无显著差异．

类似地，对单侧检验有： （2）检验假设

对应的拒绝域为

（3）检验假设

对应的拒绝域为

例设甲，乙两厂生产同样的灯泡，其寿命 $X, ~ Y$ 分别服从正态分布 $N\left(\mu_1, \sigma_1^2\right)$ ， $N\left(\mu_2, \sigma_2^2\right)$ ，已知它们寿命的标准差分别为 84 h 和 96 h ，现从两厂生产的灯泡中各取 60 只，测得平均寿命甲厂为 1295 h ，乙厂为 1230 h ，能否认为两厂生产的灯泡寿命无显著差异 （ $\alpha=0.05$ ）？

解（1）建立假设 $H_0: \mu_1=\mu_2, H_1: \mu_1 \neq \mu_2$ ． （2）选择统计量 $Z=\frac{\bar{X}-\bar{Y}}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim N(0,1)$ ． （3）对于给定的显著性水平 $\alpha$ ，确定 $k$ ，使 $P\{|Z|>k\}=\alpha$ 。 查标准正态分布表 $k=z_{\alpha / 2}=z_{0.025}=1.96$ ，从而拒绝域为 $|z|>1.96$ ． （4）由于 $\bar{x}=1295, \bar{y}=1230, \sigma_1=84, \sigma_2=96$ ，所以

故应拒绝 $H_0$ ，即认为两厂生产的灯泡寿命有显著差异。

用 $Z$ 检验法对两正态总体的均值做假设检验时，必须知道总体的方差，但在许多实际问题中，总体方差 $\sigma_1^2$ 与 $\sigma_2^2$ 往往是未知的，这时只能用如下的 $T$ 检验法．

2．方差 $\sigma_1^2, ~ \sigma_2^2$ 未知，但 $\sigma_1^2=\sigma_2^2=\sigma^2$ 关于数学期望的假设检验（ $T$ 检验法）

首先考虑双边假设检验。 （1）检验假设

由前面的讨论可知 $\bar{X}-\bar{Y} \sim N\left(\mu_1-\mu_2, \frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}\right)$ ，又 $\sigma^2$ 的一个无偏估计为

其中 $S_1^2$ 和 $S_2^2$ 分别表示 $X$ 和 $Y$ 方差．由 $S_{ w }^2$ 与 $\bar{X}-\bar{Y}$ 独立可得

采用 $T$ 检验方法，选取 $T$ 统计量为

当 $H_0$ 为真时

记其观察值为 $t$ ．相应的检验法称为 $T$ 检验法． 由于 $S_{ w }^2$ 也是 $\sigma^2$ 的无偏估计量，当 $H_0$ 成立时，$|t|$ 不应太大，当 $H_1$ 成立时，$|t|$ 有偏大的趋势，故拒绝域形式为

对于给定的显著性水平 $\alpha$ ，有

由此即得拒绝域为

根据一次抽样后得到的样本观察值 $x_1, x_2, \cdots, x_{n_1}$ 和 $y_1, y_2, \cdots, y_{n_2}$ 计算出 $T$ 的观察值 $t$ ，若 $|t| \geqslant t_{\alpha / 2}\left(n_1+n_2-2\right)$ ，则拒绝原假设 $H_0$ ，否则接受原假设 $H_0$ ．

类似地，对单侧检验有： （2）检验假设

对应的拒绝域为

（3）检验假设

对应的拒绝域为

例 某地某年高考后随机抽得 15 名男生， 12 名女生的数学考试成绩如下：

男生： 49 48 47 53 51 43 39 57 56 46 42 44 55 44 40

女生： 46 40 47 51 43 36 43 38 48 54 48 34

这 27 名学生的成绩能说明这个地区男女生的数学考试成绩不相上下吗（显著性水平 $\alpha=0.05$ ）？

解 把男生和女生数学考试的成绩分别近似地视为服从正态分布的随机变量 $X \sim N\left(\mu_1, \sigma^2\right)$与 $Y \sim N\left(\mu_2, \sigma^2\right)$ ，则本例可归结为双侧检验问题。

由题设，有 $n_1=15, n_2=12$ ，从而 $n=n_1+n_2=27$ ． 再根据例中数据算出 $\bar{x}=47.6, \bar{y}=44$ ；

由此便可计算出

取显著性水平 $\alpha=0.05$ ，查附录 D 得 $t_{\alpha / 2}(n-2)=t_{0.025}(25)=2.060$ ． 因为 $|t|=1.565 \leqslant 2.060=t_{0.025}(25)$ ，从而没有充分理由否认原假设 $H_0$ ，即认为这一地区男女生的数学考试成绩不相上下．

例 某厂铸造车间为提高缸体的耐磨性而试制了一种镍合金铸件以取代一种铜合金铸件，现从两种铸件中各抽一个样本进行硬度测试，其结果如下。

镍合金铸件 $(X): 72.0,69.5,74.0,70.5,71.8$. 铜合金铸件 $(Y): 69.8,70.0,72.0,68.5,73.0,70.0$ 。 根据以往经验知, 硬度 $X \sim N\left(\mu_1, \sigma_1^2\right), Y \sim N\left(\mu_2, \sigma_2^2\right)$, 且 $\sigma_1=\sigma_2=2$, 试在显著性水平 $\alpha=0.05$ 下, 比较镍合金铸件硬度有无显著提高. 解 根据题意假设 $H_0: \mu_1=\mu_2 \leftrightarrow H_1: \mu_1>\mu_2$, 这是一个单侧 (右侧) 检验问题, 检验统计量

拒绝域为 今 $u_{0.95}=1.645, \bar{x}=71.56, \bar{y}=70.55$, 代人得检验统计量的观测值为

因此不能拒绝 $H_0$ ，即不能认为镍合金铸件的硬度有显著提高。

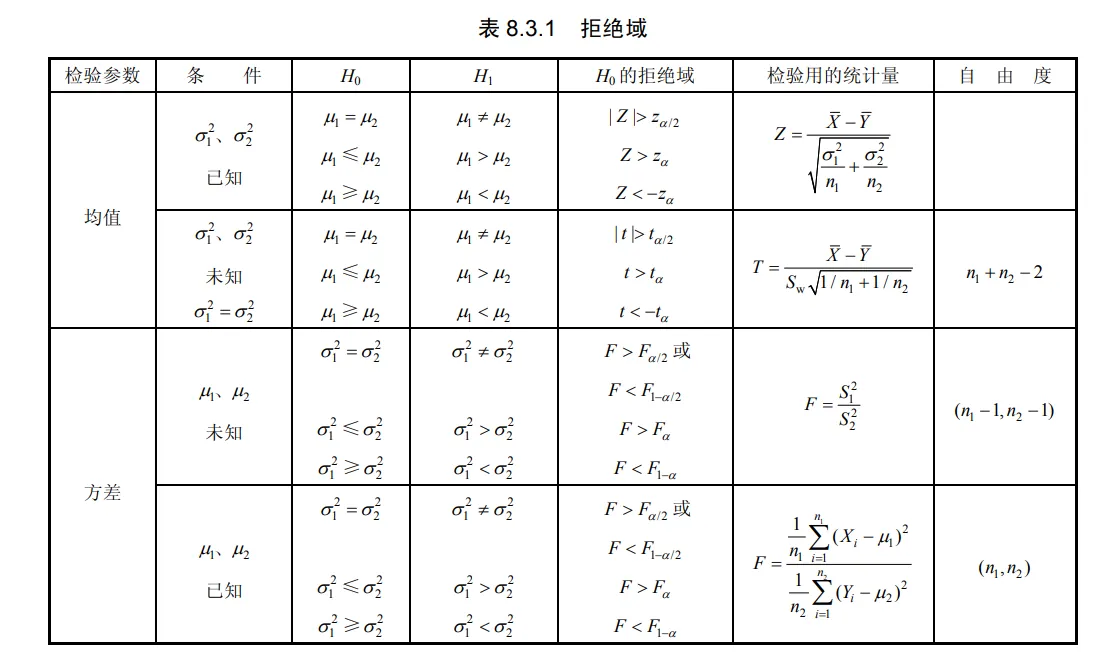
其拒绝域如表 8．3．1 所示．