2.1 LU分解与Gauss消去法 2.1.1 LU分解 Gauss 消去法本质上就是对系数矩阵 A A A A A A
A = L U , (2.2) A = L U, \tag {2.2} A = LU , ( 2.2 ) 其中 L L L U U U A A A
{ L y = b , U x = y . \left\{ \begin{array}{l} L y = b, \\ U x = y. \end{array} \right. { L y = b , Ux = y . 显然,上式中的两个三角方程组都非常容易求解
A 将一个复杂问题分解成若干相对简单的问题, 是矩阵分解的一个主要目的.
基于 LU 分解的 Gauss 消去法描述如下:
算法2.1.Gauss消去法 1: 对 A A A A = L U A = LU A = LU L L L U U U L y = b Ly = b L y = b y = L − 1 b y = L^{-1}b y = L − 1 b U x = y Ux = y Ux = y x = U − 1 y = ( L U ) − 1 b = A − 1 b x = U^{-1}y = (LU)^{-1}b = A^{-1}b x = U − 1 y = ( LU ) − 1 b = A − 1 b
我们知道, 当系数矩阵 A A A
定理2.1 (LU分解的存在性和唯一性) 矩阵 A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n L L L U U U A = L U A = LU A = LU A A A A A A
(板书)
证明. 必要性: 设 A 11 A_{11} A 11 A A A k k k 1 ≤ k ≤ n 1 \leq k \leq n 1 ≤ k ≤ n A = L U A = LU A = LU
[ A 11 A 12 A 21 A 22 ] = [ L 11 0 L 21 L 22 ] [ U 11 U 12 0 U 22 ] = [ L 11 U 11 L 11 U 12 L 21 U 11 L 21 U 12 + L 22 U 22 ] . \left[ \begin{array}{c c} A _ {1 1} & A _ {1 2} \\ A _ {2 1} & A _ {2 2} \end{array} \right] = \left[ \begin{array}{c c} L _ {1 1} & 0 \\ L _ {2 1} & L _ {2 2} \end{array} \right] \left[ \begin{array}{c c} U _ {1 1} & U _ {1 2} \\ 0 & U _ {2 2} \end{array} \right] = \left[ \begin{array}{c c} L _ {1 1} U _ {1 1} & L _ {1 1} U _ {1 2} \\ L _ {2 1} U _ {1 1} & L _ {2 1} U _ {1 2} + L _ {2 2} U _ {2 2} \end{array} \right]. [ A 11 A 21 A 12 A 22 ] = [ L 11 L 21 0 L 22 ] [ U 11 0 U 12 U 22 ] = [ L 11 U 11 L 21 U 11 L 11 U 12 L 21 U 12 + L 22 U 22 ] . 可得 A 11 = L 11 U 11 A_{11} = L_{11}U_{11} A 11 = L 11 U 11 L 11 L_{11} L 11 U 11 U_{11} U 11 A 11 A_{11} A 11
充分性: 用归纳法.
当 n = 1 n = 1 n = 1
假设结论对所有 n − 1 n - 1 n − 1 n − 1 n - 1 n − 1
考虑 n n n A A A
A = [ A 11 A 12 A 21 A 22 ] , A = \left[ \begin{array}{c c} A _ {1 1} & A _ {1 2} \\ A _ {2 1} & A _ {2 2} \end{array} \right], A = [ A 11 A 21 A 12 A 22 ] , 其中 A 11 ∈ R ( n − 1 ) × ( n − 1 ) A_{11} \in \mathbb{R}^{(n-1) \times (n-1)} A 11 ∈ R ( n − 1 ) × ( n − 1 ) A A A n − 1 n-1 n − 1 A 11 A_{11} A 11 L 11 L_{11} L 11 U 11 U_{11} U 11
A 11 = L 11 U 11 . A _ {1 1} = L _ {1 1} U _ {1 1}. A 11 = L 11 U 11 . 令
L 21 = A 21 U 11 − 1 , U 12 = L 11 − 1 A 12 , U 22 = A 22 − L 21 U 12 , L _ {2 1} = A _ {2 1} U _ {1 1} ^ {- 1}, \quad U _ {1 2} = L _ {1 1} ^ {- 1} A _ {1 2}, \quad U _ {2 2} = A _ {2 2} - L _ {2 1} U _ {1 2}, L 21 = A 21 U 11 − 1 , U 12 = L 11 − 1 A 12 , U 22 = A 22 − L 21 U 12 , 则
[ L 11 0 L 21 1 ] [ U 11 U 12 0 U 22 ] = [ L 11 U 11 L 11 U 12 L 21 U 11 U 22 + L 21 U 12 ] = [ A 11 A 12 A 21 A 22 ] = A . \left[ \begin{array}{c c} L _ {1 1} & 0 \\ L _ {2 1} & 1 \end{array} \right] \left[ \begin{array}{c c} U _ {1 1} & U _ {1 2} \\ 0 & U _ {2 2} \end{array} \right] = \left[ \begin{array}{c c} L _ {1 1} U _ {1 1} & L _ {1 1} U _ {1 2} \\ L _ {2 1} U _ {1 1} & U _ {2 2} + L _ {2 1} U _ {1 2} \end{array} \right] = \left[ \begin{array}{c c} A _ {1 1} & A _ {1 2} \\ A _ {2 1} & A _ {2 2} \end{array} \right] = A. [ L 11 L 21 0 1 ] [ U 11 0 U 12 U 22 ] = [ L 11 U 11 L 21 U 11 L 11 U 12 U 22 + L 21 U 12 ] = [ A 11 A 21 A 12 A 22 ] = A . 因此可得 A A A A = L U A = LU A = LU L ≜ [ L 11 0 L 21 1 ] L \triangleq \begin{bmatrix} L_{11} & 0 \\ L_{21} & 1 \end{bmatrix} L ≜ [ L 11 L 21 0 1 ] U ≜ [ U 11 U 12 0 U 22 ] U \triangleq \begin{bmatrix} U_{11} & U_{12} \\ 0 & U_{22} \end{bmatrix} U ≜ [ U 11 0 U 12 U 22 ] U U U A A A
由归纳法可知, 结论成立.
下面证明唯一性. 设 A A A
A = L U = L ~ U ~ , A = L U = \tilde {L} \tilde {U}, A = LU = L ~ U ~ , 其中 L L L L ~ \tilde{L} L ~ U U U U ~ \tilde{U} U ~
L − 1 L ~ = U U ~ − 1 , L ^ {- 1} \tilde {L} = U \tilde {U} ^ {- 1}, L − 1 L ~ = U U ~ − 1 , 该等式左边为下三角矩阵, 右边为上三角矩阵, 所以只能是对角矩阵. 又单位下三角矩阵的逆仍然是单位下三角矩阵, 所以 L − 1 L ~ L^{-1}\tilde{L} L − 1 L ~
L − 1 L ~ = I , L ^ {- 1} \tilde {L} = I, L − 1 L ~ = I , 即 L ~ = L , U ~ = U \tilde{L} = L, \tilde{U} = U L ~ = L , U ~ = U
记 D D D U U U A = L D ~ U ~ A = L\tilde{D}\tilde{U} A = L D ~ U ~ U ~ = D − 1 U \tilde{U} = D^{-1}U U ~ = D − 1 U
推论2.2(LDU分解)设 A ∈ R n × n A\in \mathbb{R}^{n\times n} A ∈ R n × n A A A L L L U U U D D D A = L D U A = LDU A = L D U L , U , D L,U,D L , U , D A A A A A A
对角占优情形 一般的非奇异矩阵不一定存在 LU 分解, 但如果 A A A
定理2.3 [57] 设 A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n A A A L L L
需要注意的是, 在实际计算中, 由于舍入误差的影响, 即使是严格对角占优矩阵, 如果对角占优性不是很强的话, 很有可能会失去对角占优性, 从而导致 LU 分解失败.
2.1.2 LU分解的实现 矩阵的 LU 分解可以通过初等行变换来实现. 给定矩阵
A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋱ a n 1 a n 2 … a n n ] ∈ R n × n . A = \left[ \begin{array}{c c c c} a _ {1 1} & a _ {1 2} & \dots & a _ {1 n} \\ a _ {2 1} & a _ {2 2} & \dots & a _ {2 n} \\ \vdots & & \ddots & \\ a _ {n 1} & a _ {n 2} & \dots & a _ {n n} \end{array} \right] \in \mathbb {R} ^ {n \times n}. A = a 11 a 21 ⋮ a n 1 a 12 a 22 a n 2 … … ⋱ … a 1 n a 2 n a nn ∈ R n × n . 第一步: 假定 a 11 ≠ 0 a_{11} \neq 0 a 11 = 0
L 1 = [ 1 0 0 … 0 l 21 1 0 … 0 l 31 0 1 … 0 ⋮ ⋱ l n 1 0 0 … 1 ] , 其 中 l i 1 = a i 1 a 11 , i = 2 , 3 , … , n . L _ {1} = \left[ \begin{array}{c c c c c} {{1}} & {{0}} & {{0}} & {{\dots}} & {{0}} \\ {{l _ {2 1}}} & {{1}} & {{0}} & {{\dots}} & {{0}} \\ {{l _ {3 1}}} & {{0}} & {{1}} & {{\dots}} & {{0}} \\ {{\vdots}} & {} & {} & {{\ddots}} & {} \\ {{l _ {n 1}}} & {{0}} & {{0}} & {{\dots}} & {{1}} \end{array} \right], \quad \text {其 中} \quad l _ {i 1} = \frac {a _ {i 1}}{a _ {1 1}}, i = 2, 3, \ldots , n. L 1 = 1 l 21 l 31 ⋮ l n 1 0 1 0 0 0 0 1 0 … … … ⋱ … 0 0 0 1 , 其 中 l i 1 = a 11 a i 1 , i = 2 , 3 , … , n . 易知 L 1 L_{1} L 1
L 1 − 1 = [ 1 0 0 … 0 − l 21 1 0 … 0 − l 31 0 1 … 0 ⋮ ⋱ − l n 1 0 0 … 1 ] . L _ {1} ^ {- 1} = \left[ \begin{array}{c c c c c} 1 & 0 & 0 & \dots & 0 \\ - l _ {2 1} & 1 & 0 & \dots & 0 \\ - l _ {3 1} & 0 & 1 & \dots & 0 \\ \vdots & & & \ddots & \\ - l _ {n 1} & 0 & 0 & \dots & 1 \end{array} \right]. L 1 − 1 = 1 − l 21 − l 31 ⋮ − l n 1 0 1 0 0 0 0 1 0 … … … ⋱ … 0 0 0 1 . 用 L 1 − 1 L_{1}^{-1} L 1 − 1 A A A A ( 1 ) A^{(1)} A ( 1 )
A ( 1 ) = L 1 − 1 A [ a 11 a 12 … a 1 n 0 a 22 ( 1 ) … a 2 n ( 1 ) ⋮ ⋮ ⋱ 0 a n 2 ( 1 ) … a n n ( 1 ) ] . A ^ {(1)} = L _ {1} ^ {- 1} A \left[ \begin{array}{c c c c} a _ {1 1} & a _ {1 2} & \dots & a _ {1 n} \\ 0 & a _ {2 2} ^ {(1)} & \dots & a _ {2 n} ^ {(1)} \\ \vdots & \vdots & \ddots & \\ 0 & a _ {n 2} ^ {(1)} & \dots & a _ {n n} ^ {(1)} \end{array} \right]. A ( 1 ) = L 1 − 1 A a 11 0 ⋮ 0 a 12 a 22 ( 1 ) ⋮ a n 2 ( 1 ) … … ⋱ … a 1 n a 2 n ( 1 ) a nn ( 1 ) . 即左乘 L 1 − 1 L_{1}^{-1} L 1 − 1 A A A
第二步: 类似地, 我们可以将上面的操作作用在 A ( 1 ) A^{(1)} A ( 1 ) A ( 1 ) ( 2 : n , 2 : n ) A^{(1)}(2:n,2:n) A ( 1 ) ( 2 : n , 2 : n ) a 22 ( 1 ) ≠ 0 a_{22}^{(1)} \neq 0 a 22 ( 1 ) = 0
L 2 = [ 1 0 0 … 0 0 1 0 … 0 0 l 32 1 … 0 ⋮ ⋮ ⋱ 0 l n 2 0 … 1 ] , 其 中 l i 2 = a i 2 ( 1 ) a 22 ( 1 ) , i = 3 , 4 , … , n . L _ {2} = \left[ \begin{array}{c c c c c} {{1}} & {{0}} & {{0}} & {{\dots}} & {{0}} \\ {{0}} & {{1}} & {{0}} & {{\dots}} & {{0}} \\ {{0}} & {{l _ {3 2}}} & {{1}} & {{\dots}} & {{0}} \\ {{\vdots}} & {{\vdots}} & {} & {{\ddots}} & {} \\ {{0}} & {{l _ {n 2}}} & {{0}} & {{\dots}} & {{1}} \end{array} \right], \quad \text {其 中} \quad l _ {i 2} = \frac {a _ {i 2} ^ {(1)}}{a _ {2 2} ^ {(1)}}, i = 3, 4, \ldots , n. L 2 = 1 0 0 ⋮ 0 0 1 l 32 ⋮ l n 2 0 0 1 0 … … … ⋱ … 0 0 0 1 , 其 中 l i 2 = a 22 ( 1 ) a i 2 ( 1 ) , i = 3 , 4 , … , n . 用 L 2 − 1 L_{2}^{-1} L 2 − 1 A ( 1 ) A^{(1)} A ( 1 ) A ( 2 ) A^{(2)} A ( 2 )
A ( 2 ) = L 2 − 1 A ( 1 ) = L 2 − 1 L 1 − 1 A = [ a 11 a 12 a 13 … a 1 n 0 a 22 ( 1 ) a 23 ( 1 ) … a 2 n ( 1 ) 0 0 a 33 ( 2 ) … a 3 n ( 2 ) ⋮ ⋮ ⋮ ⋱ 0 0 a n 3 ( 2 ) … a n n ( 2 ) ] . A ^ {(2)} = L _ {2} ^ {- 1} A ^ {(1)} = L _ {2} ^ {- 1} L _ {1} ^ {- 1} A = \left[ \begin{array}{c c c c c} a _ {1 1} & a _ {1 2} & a _ {1 3} & \dots & a _ {1 n} \\ 0 & a _ {2 2} ^ {(1)} & a _ {2 3} ^ {(1)} & \dots & a _ {2 n} ^ {(1)} \\ 0 & 0 & a _ {3 3} ^ {(2)} & \dots & a _ {3 n} ^ {(2)} \\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & a _ {n 3} ^ {(2)} & \dots & a _ {n n} ^ {(2)} \end{array} \right]. A ( 2 ) = L 2 − 1 A ( 1 ) = L 2 − 1 L 1 − 1 A = a 11 0 0 ⋮ 0 a 12 a 22 ( 1 ) 0 ⋮ 0 a 13 a 23 ( 1 ) a 33 ( 2 ) ⋮ a n 3 ( 2 ) … … … ⋱ … a 1 n a 2 n ( 1 ) a 3 n ( 2 ) a nn ( 2 ) . 依此类推, 假定 a k k ( k − 1 ) ≠ 0 ( k = 3 , 4 , … , n − 1 ) a_{kk}^{(k - 1)} \neq 0 (k = 3,4,\ldots ,n - 1) a kk ( k − 1 ) = 0 ( k = 3 , 4 , … , n − 1 ) L 3 , L 4 , … , L n − 1 L_{3}, L_{4}, \ldots, L_{n - 1} L 3 , L 4 , … , L n − 1
L n − 1 − 1 … L 2 − 1 L 1 − 1 A = [ a 11 a 12 a 13 … a 1 n 0 a 22 ( 1 ) a 23 ( 1 ) … a 2 n ( 1 ) 0 0 a 33 ( 2 ) … a 3 n ( 2 ) ⋮ ⋮ ⋮ ⋱ 0 0 0 … a n n ( n − 1 ) ] L _ {n - 1} ^ {- 1} \dots L _ {2} ^ {- 1} L _ {1} ^ {- 1} A = \left[ \begin{array}{c c c c c} a _ {1 1} & a _ {1 2} & a _ {1 3} & \dots & a _ {1 n} \\ 0 & a _ {2 2} ^ {(1)} & a _ {2 3} ^ {(1)} & \dots & a _ {2 n} ^ {(1)} \\ 0 & 0 & a _ {3 3} ^ {(2)} & \dots & a _ {3 n} ^ {(2)} \\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & 0 & \dots & a _ {n n} ^ {(n - 1)} \end{array} \right] L n − 1 − 1 … L 2 − 1 L 1 − 1 A = a 11 0 0 ⋮ 0 a 12 a 22 ( 1 ) 0 ⋮ 0 a 13 a 23 ( 1 ) a 33 ( 2 ) ⋮ 0 … … … ⋱ … a 1 n a 2 n ( 1 ) a 3 n ( 2 ) a nn ( n − 1 ) 为一个上三角矩阵. 我们将这个上三角矩阵记为 U U U
L ≜ L 1 L 2 … L n − 1 = [ 1 0 0 … 0 l 21 1 0 … 0 l 31 l 32 1 … 0 ⋮ ⋮ ⋱ l n 1 l n 2 l n 3 … 1 ] , (2.3) L \triangleq L _ {1} L _ {2} \dots L _ {n - 1} = \left[ \begin{array}{c c c c c} 1 & 0 & 0 & \dots & 0 \\ l _ {2 1} & 1 & 0 & \dots & 0 \\ l _ {3 1} & l _ {3 2} & 1 & \dots & 0 \\ \vdots & \vdots & & \ddots & \\ l _ {n 1} & l _ {n 2} & l _ {n 3} & \dots & 1 \end{array} \right], \tag {2.3} L ≜ L 1 L 2 … L n − 1 = 1 l 21 l 31 ⋮ l n 1 0 1 l 32 ⋮ l n 2 0 0 1 l n 3 … … … ⋱ … 0 0 0 1 , ( 2.3 ) 则可得
这就是 A A A
将上述过程写成算法,描述如下:
算法2.2.LU分解 1: Set L = I , U = 0 L = I, U = 0 L = I , U = 0 L L L U U U k = 1 k = 1 k = 1 n − 1 n - 1 n − 1 j = k j = k j = k n n n u k j = a k j % u_{kj} = a_{kj} \quad \% u kj = a kj % U U U k k k i = k + 1 i = k + 1 i = k + 1 n n n l i k = a i k / a k k l_{ik} = a_{ik} / a_{kk} l ik = a ik / a kk % \% % l i k l_{ik} l ik j = k + 1 j = k + 1 j = k + 1 n n n a i j = a i j − l i k u k j a_{ij} = a_{ij} - l_{ik}u_{kj} a ij = a ij − l ik u kj % \% % A ( i , k + 1 : n ) A(i,k + 1:n) A ( i , k + 1 : n )
11: end for
评价算法的一个主要指标是执行时间, 但这依赖于计算机硬件和编程技巧等, 因此直接给出算法执行时间是不太现实的. 所以我们通常是统计算法中算术运算 (加减乘除) 的次数. 在矩阵计算中, 大多仅仅涉及加减乘除和开方运算. 一般情况下, 加减运算次数与乘法运次数具有相同的量级, 而除法运算和开方运算次数具有更低的量级.α A B x \alpha A B x α A B x α \alpha α A , B A, B A , B x x x O ( n 3 ) \mathcal{O}(n^{3}) O ( n 3 ) α x \alpha x αx B ( α x ) B(\alpha x) B ( αx ) A ( B ( α x ) ) A(B(\alpha x)) A ( B ( αx )) O ( n 2 ) \mathcal{O}(n^{2}) O ( n 2 )
矩阵 L L L U U U 当 A A A i i i L L L i i i A A A i i i U U U i i i L L L i i i A A A i i i L L L U U U i i i A A A i i i L L L U U U A A A U U U L L L
算法2.3.LU分解(用 A A A L L L U U U 1: for k = 1 k = 1 k = 1 n − 1 n - 1 n − 1 i = k + 1 i = k + 1 i = k + 1 n n n a i k = a i k / a k k a_{ik} = a_{ik} / a_{kk} a ik = a ik / a kk j = k + 1 j = k + 1 j = k + 1 n n n a i j = a i j − a i k a k j a_{ij} = a_{ij} - a_{ik}a_{kj} a ij = a ij − a ik a kj
LU分解的运算量 由算法2.2可知,LU分解的运算量为
乘法次数: T p = ∑ k = 1 n − 1 ∑ i = k + 1 n ∑ j = k + 1 n 1 = ∑ k = 1 n − 1 ( n − k ) 2 = 1 6 ( 2 n 3 − 3 n 2 + n ) = 1 3 n 3 + O ( n 2 ) T_{p} = \sum_{k=1}^{n-1} \sum_{i=k+1}^{n} \sum_{j=k+1}^{n} 1 = \sum_{k=1}^{n-1} (n-k)^{2} = \frac{1}{6} (2n^{3}-3n^{2}+n) = \frac{1}{3} n^{3}+\mathcal{O}(n^{2}) T p = ∑ k = 1 n − 1 ∑ i = k + 1 n ∑ j = k + 1 n 1 = ∑ k = 1 n − 1 ( n − k ) 2 = 6 1 ( 2 n 3 − 3 n 2 + n ) = 3 1 n 3 + O ( n 2 )
加法次数: T a = ∑ k = 1 n − 1 ∑ i = k + 1 n ∑ j = k + 1 n 1 = 1 3 n 3 − 1 2 n 2 + 1 6 n = 1 3 n 3 + O ( n 2 ) T_{a} = \sum_{k=1}^{n-1} \sum_{i=k+1}^{n} \sum_{j=k+1}^{n} 1 = \frac{1}{3} n^{3} - \frac{1}{2} n^{2} + \frac{1}{6} n = \frac{1}{3} n^{3} + \mathcal{O}(n^{2}) T a = ∑ k = 1 n − 1 ∑ i = k + 1 n ∑ j = k + 1 n 1 = 3 1 n 3 − 2 1 n 2 + 6 1 n = 3 1 n 3 + O ( n 2 )
除法次数: T d = ∑ k = 1 n − 1 ∑ i = k + 1 n 1 = 1 2 n ( n − 1 ) = 1 2 n 2 − 1 2 n = 1 2 n 2 + O ( n ) T_{d} = \sum_{k=1}^{n-1} \sum_{i=k+1}^{n} 1 = \frac{1}{2} n(n-1) = \frac{1}{2} n^{2} - \frac{1}{2} n = \frac{1}{2} n^{2} + \mathcal{O}(n) T d = ∑ k = 1 n − 1 ∑ i = k + 1 n 1 = 2 1 n ( n − 1 ) = 2 1 n 2 − 2 1 n = 2 1 n 2 + O ( n )
因此总运算量 (含乘法、除法与加法) 为 2 3 n 3 − 1 2 n 2 − 1 6 n = 2 3 n 3 + O ( n 2 ) \frac{2}{3} n^{3} - \frac{1}{2} n^{2} - \frac{1}{6} n = \frac{2}{3} n^{3} + \mathcal{O}(n^{2}) 3 2 n 3 − 2 1 n 2 − 6 1 n = 3 2 n 3 + O ( n 2 )
数据更新顺序与计算效率 根据指标的循环次序, 算法 2.3 也称为 KIJ 型 LU 分解. 在实际计算中, 我们一般不建议使用这个算法. 因为对于指标 k k k A A A k + 1 k + 1 k + 1 n n n
如果数据是按行存储的, 如 C / C + + C / C++ C / C + +
算法2.4.LU分解(IKJ型) 1: for i = 2 i = 2 i = 2 n n n k = 1 k = 1 k = 1 i − 1 i - 1 i − 1 a i k = a i k / a k k a_{ik} = a_{ik} / a_{kk} a ik = a ik / a kk j = k + 1 j = k + 1 j = k + 1 n n n a i j = a i j − a i k a k j a_{ij} = a_{ij} - a_{ik}a_{kj} a ij = a ij − a ik a kj
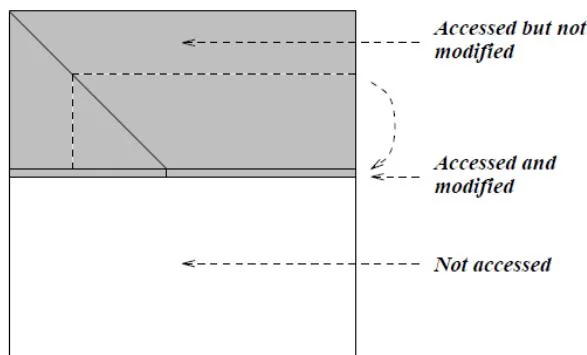
IKJ型LU分解算法可以用下图来描述. ([113,p.291])
思考:如果数据是按列存储的,如FORTRAN或MATLAB,则怎样设计算法比较好?
2.1.3 Gauss消去法 假定矩阵 A A A A = L U A = LU A = LU A x = b Ax = b A x = b
L y = b , U x = y . L y = b, \quad U x = y. L y = b , Ux = y . 这两个方程组都非常容易求解, 于是 Gauss 消去法描述如下:
算法2.5.Gauss消去法 1: 将 A A A A = L U A = LU A = LU L L L U U U L y = b Ly = b L y = b y = L − 1 b y = L^{-1}b y = L − 1 b U x = y Ux = y Ux = y x = U − 1 y = ( L U ) − 1 b = A − 1 b x = U^{-1}y = (LU)^{-1}b = A^{-1}b x = U − 1 y = ( LU ) − 1 b = A − 1 b
得到 A A A
算法2.6.回代求解 L y = b Ly = b L y = b U x = y Ux = y Ux = y
1: y 1 = b 1 / l 11 y_{1} = b_{1} / l_{11} y 1 = b 1 / l 11 L y = b Ly = b L y = b i = 2 : n i = 2:n i = 2 : n j = 1 : i − 1 j = 1 : i - 1 j = 1 : i − 1 b i = b i − l i j y j b_{i} = b_{i} - l_{ij}y_{j} b i = b i − l ij y j y i = b i / l i i y_{i} = b_{i} / l_{ii} y i = b i / l ii x n = y n / u n n x_{n} = y_{n} / u_{nn} x n = y n / u nn % \% % U x = y U x = y Ux = y i = n − 1 : − 1 : 1 i = n - 1 : -1 : 1 i = n − 1 : − 1 : 1 j = n : − 1 : i + 1 j = n: -1: i + 1 j = n : − 1 : i + 1 y i = y i − u i j x j y_{i} = y_{i} - u_{ij}x_{j} y i = y i − u ij x j x i = y i / u i i x_{i} = y_{i} / u_{ii} x i = y i / u ii
如果数据是按列存储的, 则采用列存储方式效率会高一些. 下面是以 U x = y Ux = y Ux = y
算法2.7. 向后回代求解 U x = y Ux = y Ux = y
1: for k = n : − 1 : 1 k = n : -1 : 1 k = n : − 1 : 1 x k = y k / u k k x_{k} = y_{k} / u_{kk} x k = y k / u kk i = k − 1 : − 1 : 1 i = k - 1: -1:1 i = k − 1 : − 1 : 1 y i = y i − x k u i k y_{i} = y_{i} - x_{k}u_{ik} y i = y i − x k u ik
计算复杂度 这两个算法的运算量: 乘法和加法均 n ( n − 1 ) n(n - 1) n ( n − 1 ) 2 n 2n 2 n 2 3 n 3 + O ( n 2 ) \frac{2}{3} n^3 + \mathcal{O}(n^2) 3 2 n 3 + O ( n 2 )
可以证明, 以上两个算法都是向后稳定的 (componentwise backward stable) [70].
2.1.4 选主元LU分解 在 LU 分解过程中, 我们称 a k k ( k − 1 ) a_{kk}^{(k-1)} a kk ( k − 1 ) a k k ( k − 1 ) = 0 a_{kk}^{(k-1)} = 0 a kk ( k − 1 ) = 0 a k k ( k − 1 ) a_{kk}^{(k-1)} a kk ( k − 1 ) ∣ a k k ( k − 1 ) ∣ |a_{kk}^{(k-1)}| ∣ a kk ( k − 1 ) ∣
例2.1 用LU分解求解线性方程组 A x = b Ax = b A x = b A = [ 0.02 61.3 3.43 − 8.5 ] , b = [ 61.5 25.8 ] A = \begin{bmatrix} 0.02 & 61.3 \\ 3.43 & -8.5 \end{bmatrix}, b = \begin{bmatrix} 61.5 \\ 25.8 \end{bmatrix} A = [ 0.02 3.43 61.3 − 8.5 ] , b = [ 61.5 25.8 ]
解.根据LU分解待定系数法,设
A = L U = [ 1 0 l 21 1 ] [ u 11 u 12 0 u 22 ] . A = L U = \left[ \begin{array}{c c} 1 & 0 \\ l _ {2 1} & 1 \end{array} \right] \left[ \begin{array}{c c} u _ {1 1} & u _ {1 2} \\ 0 & u _ {2 2} \end{array} \right]. A = LU = [ 1 l 21 0 1 ] [ u 11 0 u 12 u 22 ] . 直接比较等式两边可得
u 11 = a 11 = 0.02 , u 12 = a 12 = 61.3 , l 21 = a 21 / u 11 = 3.43 / 0.02 ≈ 172 , u 22 = a 22 − l 21 u 12 ≈ − 8.5 − 1.05 × 10 4 ≈ − 1.05 × 10 4 , \begin{array}{l} u _ {1 1} = a _ {1 1} = 0. 0 2, u _ {1 2} = a _ {1 2} = 6 1. 3, \\ l _ {2 1} = a _ {2 1} / u _ {1 1} = 3. 4 3 / 0. 0 2 \approx 1 7 2, \\ u _ {2 2} = a _ {2 2} - l _ {2 1} u _ {1 2} \approx - 8. 5 - 1. 0 5 \times 1 0 ^ {4} \approx - 1. 0 5 \times 1 0 ^ {4}, \\ \end{array} u 11 = a 11 = 0.02 , u 12 = a 12 = 61.3 , l 21 = a 21 / u 11 = 3.43/0.02 ≈ 172 , u 22 = a 22 − l 21 u 12 ≈ − 8.5 − 1.05 × 1 0 4 ≈ − 1.05 × 1 0 4 , 解方程组 L y = b Ly = b L y = b
y 1 = 61.5 , y 2 = b 2 − l 21 y 1 ≈ − 1.06 × 10 4 . y _ {1} = 6 1. 5, \quad y _ {2} = b _ {2} - l _ {2 1} y _ {1} \approx - 1. 0 6 \times 1 0 ^ {4}. y 1 = 61.5 , y 2 = b 2 − l 21 y 1 ≈ − 1.06 × 1 0 4 . 解方程组 U x = y Ux = y Ux = y
x 2 = y 2 / u 22 ≈ 1.01 , x 1 = ( y 1 − u 12 x 2 ) / u 11 ≈ − 0.413 / u 11 ≈ − 20.7 x _ {2} = y _ {2} / u _ {2 2} \approx 1. 0 1, \quad x _ {1} = \left(y _ {1} - u _ {1 2} x _ {2}\right) / u _ {1 1} \approx - 0. 4 1 3 / u _ {1 1} \approx - 2 0. 7 x 2 = y 2 / u 22 ≈ 1.01 , x 1 = ( y 1 − u 12 x 2 ) / u 11 ≈ − 0.413/ u 11 ≈ − 20.7 □
事实上, 精确解为 x 1 = 10.0 x_{1} = 10.0 x 1 = 10.0 x 2 = 1.00 x_{2} = 1.00 x 2 = 1.00 x 1 x_{1} x 1 ∣ a 11 ∣ \left|a_{11}\right| ∣ a 11 ∣
选主元是通过利用置换矩阵(也称排列矩阵)对行进行交换来实现的. 首先介绍置换矩阵的一些基本性质.
引理2.4设 P ∈ R n × n P\in \mathbb{R}^{n\times n} P ∈ R n × n A ∈ R n × n A\in \mathbb{R}^{n\times n} A ∈ R n × n
(1) P A PA P A A A A A P AP A P A A A P − 1 = P T P^{-1} = P^{\mathsf{T}} P − 1 = P T P P P det ( P ) = ± 1 \operatorname{det}(P) = \pm 1 det ( P ) = ± 1
定理2.5 (选主元LU分解的存在性) 设 A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n P L , P R P_L, P_R P L , P R L L L U U U
P L A P R = L U . P _ {L} A P _ {R} = L U. P L A P R = LU . (板书)
证明. 用归纳法
当 n = 1 n = 1 n = 1 P L = P R = L = 1 , U = A P_L = P_R = L = 1, U = A P L = P R = L = 1 , U = A
假设结论对所有 n − 1 n - 1 n − 1
考虑 n n n A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n A A A P 1 P_{1} P 1 P 2 P_{2} P 2
P 1 A P 2 = [ a 11 A 12 A 21 A 22 ] , P _ {1} A P _ {2} = \left[ \begin{array}{c c} a _ {1 1} & A _ {1 2} \\ A _ {2 1} & A _ {2 2} \end{array} \right], P 1 A P 2 = [ a 11 A 21 A 12 A 22 ] , 其中 a 11 ≠ 0 , A 22 ∈ R ( n − 1 ) × ( n − 1 ) a_{11} \neq 0, A_{22} \in \mathbb{R}^{(n-1) \times (n-1)} a 11 = 0 , A 22 ∈ R ( n − 1 ) × ( n − 1 )
u 11 = a 11 , U 12 = A 12 , L 21 = A 21 / a 11 , U 22 = A 22 − L 21 U 12 . u _ {1 1} = a _ {1 1}, \quad U _ {1 2} = A _ {1 2}, \quad L _ {2 1} = A _ {2 1} / a _ {1 1}, \quad U _ {2 2} = A _ {2 2} - L _ {2 1} U _ {1 2}. u 11 = a 11 , U 12 = A 12 , L 21 = A 21 / a 11 , U 22 = A 22 − L 21 U 12 . 则 u 11 ≠ 0 u_{11} \neq 0 u 11 = 0
[ 1 0 L 21 I ] [ u 11 U 12 0 U 22 ] = [ a 11 A 12 A 21 A 22 ] = P 1 A P 2 . \left[ \begin{array}{c c} 1 & 0 \\ L _ {2 1} & I \end{array} \right] \left[ \begin{array}{c c} u _ {1 1} & U _ {1 2} \\ 0 & U _ {2 2} \end{array} \right] = \left[ \begin{array}{c c} a _ {1 1} & A _ {1 2} \\ A _ {2 1} & A _ {2 2} \end{array} \right] = P _ {1} A P _ {2}. [ 1 L 21 0 I ] [ u 11 0 U 12 U 22 ] = [ a 11 A 21 A 12 A 22 ] = P 1 A P 2 . 两边取行列式可得
0 ≠ det ( P 1 A P 2 ) = det ( [ 1 0 L 21 I ] ) ⋅ det ( [ u 11 U 12 0 U 22 ] ) = a 11 ⋅ det ( U 22 ) . 0 \neq \det (P _ {1} A P _ {2}) = \det \left(\left[ \begin{array}{c c} 1 & 0 \\ L _ {2 1} & I \end{array} \right]\right) \cdot \det \left(\left[ \begin{array}{c c} u _ {1 1} & U _ {1 2} \\ 0 & U _ {2 2} \end{array} \right]\right) = a _ {1 1} \cdot \det (U _ {2 2}). 0 = det ( P 1 A P 2 ) = det ( [ 1 L 21 0 I ] ) ⋅ det ( [ u 11 0 U 12 U 22 ] ) = a 11 ⋅ det ( U 22 ) . 所以 det ( U 22 ) ≠ 0 \operatorname{det}(U_{22}) \neq 0 det ( U 22 ) = 0 U 22 ∈ R ( n − 1 ) × ( n − 1 ) U_{22} \in \mathbb{R}^{(n-1) \times (n-1)} U 22 ∈ R ( n − 1 ) × ( n − 1 ) P ~ L ∈ R ( n − 1 ) × ( n − 1 ) \tilde{P}_L \in \mathbb{R}^{(n-1) \times (n-1)} P ~ L ∈ R ( n − 1 ) × ( n − 1 ) P ~ R ∈ R ( n − 1 ) × ( n − 1 ) \tilde{P}_R \in \mathbb{R}^{(n-1) \times (n-1)} P ~ R ∈ R ( n − 1 ) × ( n − 1 )
P ~ L U 22 P ~ R = L ~ 22 U ~ 22 , \tilde {P} _ {L} U _ {2 2} \tilde {P} _ {R} = \tilde {L} _ {2 2} \tilde {U} _ {2 2}, P ~ L U 22 P ~ R = L ~ 22 U ~ 22 , 其中 L ~ 22 \tilde{L}_{22} L ~ 22 U ~ 22 \tilde{U}_{22} U ~ 22
P L = [ 1 0 0 P ~ L ] P 1 , P R = P 2 [ 1 0 0 P ~ R ] , P _ {L} = \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {L} \end{array} \right] P _ {1}, \quad P _ {R} = P _ {2} \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {R} \end{array} \right], P L = [ 1 0 0 P ~ L ] P 1 , P R = P 2 [ 1 0 0 P ~ R ] , 则有
P L A P R = [ 1 0 0 P ~ L ] P 1 A P 2 [ 1 0 0 P ~ R ] = [ 1 0 0 P ~ L ] [ 1 0 L 21 I ] [ u 11 U 12 0 U 22 ] [ 1 0 0 P ~ R ] = [ 1 0 P ~ L L 21 P ~ L ] [ u 11 U 12 0 P ~ L T L ~ 22 U ~ 22 P ~ R T ] [ 1 0 0 P ~ R ] = [ 1 0 P ~ L L 21 P ~ L ] [ 1 0 0 P ~ 1 T L ~ 22 ] [ u 11 U 12 0 U ~ 22 P ~ R T ] [ 1 0 0 P ~ R ] = [ 1 0 P ~ L L 21 L ~ 22 ] [ u 11 U 12 P ~ R 0 U ~ 22 ] ≜ L U , \begin{array}{l} P _ {L} A P _ {R} = \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {L} \end{array} \right] P _ {1} A P _ {2} \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {R} \end{array} \right] \\ = \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {L} \end{array} \right] \left[ \begin{array}{c c} 1 & 0 \\ L _ {2 1} & I \end{array} \right] \left[ \begin{array}{c c} u _ {1 1} & U _ {1 2} \\ 0 & U _ {2 2} \end{array} \right] \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {R} \end{array} \right] \\ = \left[ \begin{array}{c c} 1 & 0 \\ \tilde {P} _ {L} L _ {2 1} & \tilde {P} _ {L} \end{array} \right] \left[ \begin{array}{c c} u _ {1 1} & U _ {1 2} \\ 0 & \tilde {P} _ {L} ^ {\mathsf {T}} \tilde {L} _ {2 2} \tilde {U} _ {2 2} \tilde {P} _ {R} ^ {\mathsf {T}} \end{array} \right] \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {R} \end{array} \right] \\ = \left[ \begin{array}{c c} 1 & 0 \\ \tilde {P} _ {L} L _ {2 1} & \tilde {P} _ {L} \end{array} \right] \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {1} ^ {\mathsf {T}} \tilde {L} _ {2 2} \end{array} \right] \left[ \begin{array}{c c} u _ {1 1} & U _ {1 2} \\ 0 & \tilde {U} _ {2 2} \tilde {P} _ {R} ^ {\mathsf {T}} \end{array} \right] \left[ \begin{array}{c c} 1 & 0 \\ 0 & \tilde {P} _ {R} \end{array} \right] \\ = \left[ \begin{array}{c c} 1 & 0 \\ \tilde {P} _ {L} L _ {2 1} & \tilde {L} _ {2 2} \end{array} \right] \left[ \begin{array}{c c} u _ {1 1} & U _ {1 2} \tilde {P} _ {R} \\ 0 & \tilde {U} _ {2 2} \end{array} \right] \triangleq L U, \\ \end{array} P L A P R = [ 1 0 0 P ~ L ] P 1 A P 2 [ 1 0 0 P ~ R ] = [ 1 0 0 P ~ L ] [ 1 L 21 0 I ] [ u 11 0 U 12 U 22 ] [ 1 0 0 P ~ R ] = [ 1 P ~ L L 21 0 P ~ L ] [ u 11 0 U 12 P ~ L T L ~ 22 U ~ 22 P ~ R T ] [ 1 0 0 P ~ R ] = [ 1 P ~ L L 21 0 P ~ L ] [ 1 0 0 P ~ 1 T L ~ 22 ] [ u 11 0 U 12 U ~ 22 P ~ R T ] [ 1 0 0 P ~ R ] = [ 1 P ~ L L 21 0 L ~ 22 ] [ u 11 0 U 12 P ~ R U ~ 22 ] ≜ LU , 其中 L L L U U U A A A
因此, 由数学归纳法可知, 结论成立.
定理2.5也可以利用定理2.1的结论来证明,见习题2.3P L P_L P L P R P_R P R
置换矩阵的选取 问题: 第 k k k P L ( k ) P_L^{(k)} P L ( k ) P R ( k ) P_R^{(k)} P R ( k )
选法一.选取 P L ( k ) P_L^{(k)} P L ( k ) P R ( k ) P_R^{(k)} P R ( k )
选法二.选取 P L ( k ) P_L^{(k)} P L ( k ) P R ( k ) P_R^{(k)} P R ( k ) k k k k k k n n n P R ( k ) = I P_R^{(k)} = I P R ( k ) = I
(1) GECP 比 GEPP 更稳定, 但工作量太大, 在实际应用中通常使用 GEPP 算法.L L L
算法2.8.部分选主元LU分解 1: p = 1 : n p = 1:n p = 1 : n % \% % k = 1 k = 1 k = 1 n − 1 n - 1 n − 1
3: [ a max , l ] = max k < i < n ∣ a i k ∣ % [a_{\max}, l] = \max_{k < i < n} |a_{ik}| \quad \% [ a m a x , l ] = max k < i < n ∣ a ik ∣ % l l l l ≠ k l \neq k l = k
5: for j = 1 j = 1 j = 1 n n n a t m p = a k j , a k j = a l j , a l j = a t m p % a_{tmp} = a_{kj}, a_{kj} = a_{lj}, a_{lj} = a_{tmp} \quad \% a t m p = a kj , a kj = a l j , a l j = a t m p % A A A k k k l l l
7: end for
8: p t m p = p ( k ) , p ( k ) = p ( l ) , p ( l ) = p t m p % p_{tmp} = p(k), p(k) = p(l), p(l) = p_{tmp} \quad \% p t m p = p ( k ) , p ( k ) = p ( l ) , p ( l ) = p t m p %
10: for i = k + 1 i = k + 1 i = k + 1 n n n a i k = a i k / a k k a_{ik} = a_{ik} / a_{kk} a ik = a ik / a kk j = k + 1 j = k + 1 j = k + 1 n n n a i j = a i j − a i k a k j a_{ij} = a_{ij} - a_{ik}a_{kj} a ij = a ij − a ik a kj
相应的MATLAB程序见LE_PLU.m.
例2.2 用部分选主元LU分解求解线性方程组 A x = b Ax = b A x = b A = [ 0.02 61.3 3.43 − 8.5 ] A = \begin{bmatrix} 0.02 & 61.3 \\ 3.43 & -8.5 \end{bmatrix} A = [ 0.02 3.43 61.3 − 8.5 ] b = [ 61.5 25.8 ] b = \begin{bmatrix} 61.5 \\ 25.8 \end{bmatrix} b = [ 61.5 25.8 ]
求在运算过程中保留3位有效数字
(板书)
解.由于 ∣ a 21 ∣ > ∣ a 11 ∣ |a_{21}| > |a_{11}| ∣ a 21 ∣ > ∣ a 11 ∣ P = [ 0 1 1 0 ] , P = \left[ \begin{array}{ll}0 & 1\\ 1 & 0 \end{array} \right], P = [ 0 1 1 0 ] , A ~ = P A = [ 3.43 − 8.5 0.02 61.3 ] \tilde{A} = PA = \left[ \begin{array}{ll}3.43 & -8.5\\ 0.02 & 61.3 \end{array} \right] A ~ = P A = [ 3.43 0.02 − 8.5 61.3 ]
A ~ = L U = [ 1 0 l 21 1 ] [ u 11 u 12 0 u 22 ] . \tilde {A} = L U = \left[ \begin{array}{c c} 1 & 0 \\ l _ {2 1} & 1 \end{array} \right] \left[ \begin{array}{c c} u _ {1 1} & u _ {1 2} \\ 0 & u _ {2 2} \end{array} \right]. A ~ = LU = [ 1 l 21 0 1 ] [ u 11 0 u 12 u 22 ] . 直接比较等式两边可得
u 11 = a ~ 11 = 3.43 , u 12 = a ~ 12 = − 8.5 , l 21 = a ~ 21 / u 11 ≈ 5.83 × 10 − 3 , u 22 = a ~ 22 − l 21 u 12 ≈ 61.3 + 0.0496 ≈ 61.3 , \begin{array}{l} u _ {1 1} = \tilde {a} _ {1 1} = 3. 4 3, u _ {1 2} = \tilde {a} _ {1 2} = - 8. 5, \\ l _ {2 1} = \tilde {a} _ {2 1} / u _ {1 1} \approx 5. 8 3 \times 1 0 ^ {- 3}, \\ u _ {2 2} = \tilde {a} _ {2 2} - l _ {2 1} u _ {1 2} \approx 6 1. 3 + 0. 0 4 9 6 \approx 6 1. 3, \\ \end{array} u 11 = a ~ 11 = 3.43 , u 12 = a ~ 12 = − 8.5 , l 21 = a ~ 21 / u 11 ≈ 5.83 × 1 0 − 3 , u 22 = a ~ 22 − l 21 u 12 ≈ 61.3 + 0.0496 ≈ 61.3 , 即
P A ≈ [ 1.00 0 5.83 × 10 − 3 1.00 ] [ 3.43 − 8.50 0 61.3 ] . P A \approx \left[ \begin{array}{c c} 1. 0 0 & 0 \\ 5. 8 3 \times 1 0 ^ {- 3} & 1. 0 0 \end{array} \right] \left[ \begin{array}{c c} 3. 4 3 & - 8. 5 0 \\ 0 & 6 1. 3 \end{array} \right]. P A ≈ [ 1.00 5.83 × 1 0 − 3 0 1.00 ] [ 3.43 0 − 8.50 61.3 ] . 解方程组 L y = P b Ly = Pb L y = P b
y 1 = 25.8 , y 2 ≈ 61.2. y _ {1} = 2 5. 8, \quad y _ {2} \approx 6 1. 2. y 1 = 25.8 , y 2 ≈ 61.2. 解方程组 U x = y Ux = y Ux = y
x 2 = y 2 / u 22 ≈ 0.998 , x 1 = ( y 1 − u 12 x 2 ) / u 11 ≈ 10.0. x _ {2} = y _ {2} / u _ {2 2} \approx 0. 9 9 8, \quad x _ {1} = (y _ {1} - u _ {1 2} x _ {2}) / u _ {1 1} \approx 1 0. 0. x 2 = y 2 / u 22 ≈ 0.998 , x 1 = ( y 1 − u 12 x 2 ) / u 11 ≈ 10.0. 与精确解 x 1 = 10 , x 2 = 1 x_{1} = 10, x_{2} = 1 x 1 = 10 , x 2 = 1
2.1.5 矩阵求逆 我们可以通过部分选主元 LU 分解来计算矩阵的逆. 设 P A = L U PA = LU P A = LU
A − 1 = U − 1 L − 1 P , A ^ {- 1} = U ^ {- 1} L ^ {- 1} P, A − 1 = U − 1 L − 1 P , 等价于求解下面 2 n 2n 2 n
L y i = P e i , U x i = y i , i = 1 , 2 , … , n . L y _ {i} = P e _ {i}, \quad U x _ {i} = y _ {i}, \quad i = 1, 2, \dots , n. L y i = P e i , U x i = y i , i = 1 , 2 , … , n .
思考:也可以分别计算 L − 1 L^{-1} L − 1 U − 1 U^{-1} U − 1
2.1.6 分块LU分解 为了提高计算效率, 实际计算中通常采用分块 LU 分解, 即
A = [ A 11 A 12 … A 1 p A 21 A 22 … A 2 p ⋮ ⋱ ⋮ A p 1 A p 2 … A p p ] = [ I 1 L 21 I 2 ⋮ ⋱ ⋱ L p 1 … L p , p − 1 I p ] [ U 11 U 12 … U 1 p U 22 … U 2 p ⋱ ⋮ U p p ] = L U , \boldsymbol {A} = \left[ \begin{array}{c c c c} A _ {1 1} & A _ {1 2} & \dots & A _ {1 p} \\ A _ {2 1} & A _ {2 2} & \dots & A _ {2 p} \\ \vdots & & \ddots & \vdots \\ A _ {p 1} & A _ {p 2} & \dots & A _ {p p} \end{array} \right] = \left[ \begin{array}{c c c c} I _ {1} & & & \\ L _ {2 1} & I _ {2} & & \\ \vdots & \ddots & \ddots & \\ L _ {p 1} & \dots & L _ {p, p - 1} & I _ {p} \end{array} \right] \left[ \begin{array}{c c c c} U _ {1 1} & U _ {1 2} & \dots & U _ {1 p} \\ & U _ {2 2} & \dots & U _ {2 p} \\ & & \ddots & \vdots \\ & & & U _ {p p} \end{array} \right] = \boldsymbol {L U}, A = A 11 A 21 ⋮ A p 1 A 12 A 22 A p 2 … … ⋱ … A 1 p A 2 p ⋮ A pp = I 1 L 21 ⋮ L p 1 I 2 ⋱ … ⋱ L p , p − 1 I p U 11 U 12 U 22 … … ⋱ U 1 p U 2 p ⋮ U pp = LU , 其中 A i i A_{ii} A ii
与定理2.1相类似, 对于分块LU分解, 我们有下面的结论
定理2.6(分块LU分解的存在性和唯一性)矩阵 A \mathbf{A} A A \mathbf{A} A
几点注记 分块LU分解不是LU分解,若 A A A A i i A_{ii} A ii