5.7 扰动分析
设 A∈Rn×n 是对称矩阵, 则有下面的谱分解
定理5.15 设 A∈Rn×n 是对称矩阵. 则存在一个正交矩阵 Q 使得
A=QΛQT, 其中 Λ=diag(λ1,λ2,…,λn) 是一个实对角矩阵.
这里的 λi 就是 A 的特征值, 我们假设 λ1≥λ2≥⋯≥λn . 令 Q=[q1,q2,…,qn] , 则 qi 就是 λi 对应的单位正交特征向量.
关于对称矩阵特征值问题的扰动理论, 这里只做一些简单介绍, 若要深入了解这方面的信息, 可以参考 [73, 74, 122, 148].
5.7.1 特征值与Rayleigh商
定义5.2设 A∈Rn×n 是对称矩阵,向量 x∈Rn 非零,则 x 关于 A 的Rayleigh商定义为
ρ(x,A)=x⊤xx⊤Ax.(5.13) 有时简记为 ρ(x)
下面是关于实对称矩阵 Rayleigh 商的一些基本性质:
(1) ρ(αx)=ρ(x),∀α∈R,α=0;
(2) ρ(qi)=λi,i=1,2,…,n ;
(3) 设 x=α1q1+α2q2+⋯+αnqn ,则
ρ(x)=α12+α22+⋯+αn2α12λ1+α22λ2+⋯+αn2λn; (4) λn≤ρ(x)≤λ1,∣ρ(x)∣≤∥A∥2.
实对称矩阵的特征值与 Rayleigh 商之间的一个重要性质是 Courant-Fischer 极小极大定理.
定理5.16 (Courant-Fischer) 设 A∈Rn×n 是对称矩阵, 其特征值为 λ1≥λ2≥⋯≥λn , 则有
λk=U∈Sknmaxx∈U,x=0minxTxxTAx=V∈Sn−k+1nminx∈V,x=0maxxTxxTAx, 其中 Sin 表示 Rn 中所有 i 维子空间构成的集合. 当
U=span{q1,…,qk},V=span{qk,…,qn},x=qk 时, 上式中的等号成立.
(板书)
证明. 设 U∈Skn 和 V∈Sn−k+1n 分别为 Rn 中任意的 k 和 n−k+1 维子空间. 由于
dimU+dimV=n+1>n, 可得
U∩V={0}. 故存在非零向量 x~∈U∩V. 所以有
x∈U,x=0minρ(x)≤ρ(x~)≤x∈V,x=0maxρ(x). 由 U 和 V 的任意性可知,
U∈Sknmaxx∈U,x=0minρ(x)≤V∈Sn−k+1nminx∈V,x=0maxρ(x).(5.14) 取 U=span{q1,…,qk} , 则 U 中的任意向量都可写成 x=α1q1+⋯+αkqk , 此时
ρ(x)=xTxxTAx=α12+⋯+αk2α12λ1+⋯+αk2λk≥∑i=1kαi2∑i=1kαi2λk=λk, 即
U∈Sknmaxx∈U,x=0minρ(x)≥λk.(5.15) 同理, 取 V=span{qk,…,qn} , 则 V 中的任意向量都可写成 x=αkqk+⋯+αnqn , 此时
ρ(x)=xTxxTAx=αk2+⋯+αn2αk2λk+⋯+αn2λn≤∑i=knαi2∑i=knαi2λk=λk, 即
V∈Sn−k+1nminx∈V,x=0maxρ(x)≤λk.(5.16) 由 (\refeq:1) , (\refeq:2) , (\refeq:3) 可知,定理结论成立
该结论在复数域中也成立[73].
当 k=1 和 k=n 时, 就可以得到下面的定理
定理5.17 (Rayleigh-Ritz) 设 A∈Rn×n 是对称矩阵, 其特征值为 λ1≥λ2≥⋯≥λn , 则有
λ1=x∈Rn,x=0maxxTxxTAx,λn=x∈Rn,x=0minxTxxTAx. 由极小极大定理, 我们可以得到下面的特征值分隔定理
定理5.18(分隔定理)设 A∈Rn×n 是对称矩阵, B=QTAQ ,其中 Q∈Rn×(n−1) 满足 QTQ=In−1 .再设 A 和 B 的特征值分别为
λ1≥λ2≥⋯≥λn和λ~1≥λ~2≥⋯≥λ~n−1, 则有
λ1≥λ~1≥λ2≥λ~2⋯≥λ~n−1≥λn. 特别地, 在定理 5.18 中, 取 Q=[e1,…,ei−1,ei+1,…,en] , 则可以得到下面的结论.
推论5.19设 A∈Rn×n 是对称矩阵, A~ 是 A 的一个 n−1 阶主子矩阵, A 和 A~ 的特征值分别为
λ1≥λ2≥⋯≥λn和λ~1≥λ~2≥⋯≥λ~n−1, 则有
λ1≥λ~1≥λ2≥λ~2⋯≥λ~n−1≥λn. 反复应用上面的推论, 即可得到下面的结论
推论5.20 设 A∈Rn×n 是对称矩阵, A~ 是 A 的一个 k 阶主子矩阵 (1≤k≤n−1) , A 和 A~ 的特征值分别为
λ1≥λ2≥⋯≥λn和λ~1≥λ~2≥⋯≥λ~k, 则有
λi≥λ~i≥λn−k+i,i=1,2,…,k. 5.7.2 对称矩阵特征值的扰动分析
设 A∈Rn×n 是对称矩阵, 扰动矩阵 E∈Rn×n 也是对称矩阵, 下面讨论 A+E 的特征值与 A 的特征值之间的关系.
由极小极大定理, 我们可以证明下面的性质.
定理5.21 设 A∈Rn×n 和 B=A+E∈Rn×n 都是对称矩阵, 其特征值分别为
λ1≥λ2≥⋯≥λn和λ~1≥λ~2≥⋯≥λ~n. 假定 E 的最大和最小特征值分别为 μ1 和 μn , 则有
λi+μ1≥λ~i≥λi+μn,i=1,2,…,n. (板书)
证明. 由 Courant-Fischer 定理 5.16 和 Rayleigh-Ritz 定理 5.17 可知
λ~i=minV∈Sn−i+1nmaxx∈V,x=0xTxxTBx=minV∈Sn−i+1nmaxx∈V,x=0(xTxxTAx+xTxxTEx)≤minV∈Sn−i+1nmaxx∈V,x=0(x⊤xx⊤Ax+μ1)=minV∈Sn−i+1nmaxx∈V,x=0xTxxTAx+μ1=λi+μ1. 同理可得
λ~i=maxU∈Sinminx∈U,x=0xTxxTBx=maxU∈Sinminx∈U,x=0(xTxxTAx+xTxxTEx)≥maxU∈Sinminx∈U,x=0(x⊤xx⊤Ax+μn) =maxU∈Sinminx∈U,x=0xTxxTAx+μn=λi+μn. 所以定理结论成立.

根据这个定理, 我们立即可以得到下面的 Weyl 定理
定理5.22 (Weyl) 设 A∈Rn×n 和 B=A+E∈Rn×n 都是对称矩阵, 其特征值分别为 λ1≥λ2≥⋯≥λn 和 λ~1≥λ~2≥⋯≥λ~n , 则
λ~j−λj≤∥E∥2,j=1,2,…,n. 该定理的结论可以推广到奇异值情形. 我们首先给出下面的引理
引理5.23 设 A∈Rm×n ( m≥n ) 的奇异值分解为 A=UΣV ,其中 U=[u1,…,un]∈Rm×n 为列正交矩阵, V=[v1,…,vn]∈Rn×n 为正交矩阵, Σ=diag(σ1,…,σn) . 将 U 扩展成 n×n 的正交矩阵 [U,U~]=[u1,…,un,u~1,…,u~m−n] ,令
H=[0AAT0]∈R(m+n)×(m+n), 则 H 对称, 且特征值为 ±σi 和0(其中0至少为 m−n 重特征值), 对应的特征向量分别为 22[vi±ui],i=1,2,…,n, 和 [0u~j],j=1,2,…,m−n.
(留作课外自习, 直接代入验证即可)
由上面的引理和Weyl定理5.22立即可得
定理5.24 设 A,B∈Rm×n ( m≥n ), 它们的奇异值分别为 σ1≥σ2≥⋯≥σn 和 σ~1≥σ~2≥⋯≥σ~n . 则
∣σ~j−σj∣≤∥B−A∥2,j=1,2,…,n. 最后给出一个基于F-范数的扰动性质[73].
定理5.25 设 A,E∈Cn×n 且 A 是Hermite的, A+E 是正规矩阵. 并设 A 的特征值满足
λ1≥λ2≥⋯≥λn, A+E 的特征值 λ~1,λ~2,…,λ~n 满足
Re(λ~1)≥Re(λ~2)≥⋯≥Re(λ~n). 则
i=1∑nλ~i−λi2≤∥E∥F2. 5.7.3 对称矩阵特征向量的扰动
定义5.3 设 A∈Rn×n 的特征值为 λ1≥λ2≥⋯≥λn , 则 λi 与其余特征值之间的间隙 (gap) 定义为
gap(λi,A)=j=imin∣λj−λi∣. 有时简记为 gap(λi)
特征向量的敏感性依赖于其对应的特征值的 gap, 一般来说, gap 越小, 特征向量越敏感.
例5.2 设
A=[1+g1],E=[0εε0],(0<ε<g) 则 A 的特征值为 λ1=1+g,λ2=1 , 对应的单位特征向量为 q1=e1,q2=e2 . 当 ε 充分小时, A+E 的特征值为 λ^1,2=1+(g±g2+4ε2)/2 , 对应的单位特征向量为
q^1=β1⋅[1+4ε2/g2−11]=β1⋅[(1+2ε2/g2)2−4(ε/g)4−11]≈β1⋅[2ε/g(1+2ε2/g2)−11]=1+ε2/g21[1ε/g], q^2=β2⋅2ε/g−1+4ε2/g2−11≈1+ε2/g21[−ε/g1], 其中 β1,β2 为规范化因子.故特征向量的扰动约为 ε/g ,与特征值的间隙 gap(λi,A)=g 成反比
定理5.26 设 A=QΛQT 和 A+E=Q~Λ~Q~T 分别为对称矩阵 A∈Rn×n 和 A+E∈Rn×n 的特征值分解, 其中 Q=[q1,q2,…,qn] 和 Q~=[q~1,q~2,…,q~n] 均为正交矩阵, 且 q~i 为 qi 对应的扰动特征向量. 用 θi 表示 qi 和 q~i 之间的锐角, 则当 gap(λi,A)>0 时
21sin2θi≤gap(λi,A)∥E∥2. 类似地, 当 gap(λ~i,A+E)>0 时
21sin2θi≤gap(λ~i,A+E)∥E∥2. (留作课外自习)
证明. 如右图所示, 令 d=q~i/cosθi−qi , 即 q~i=(qi+d)cosθi . 则
dTqi=0,tanθi=∥d∥2,secθi=∥qi+d∥2. 令 η=λ~i−λi ,由 (A+E)q~i=λ~iq~i 可得
(A+E)(qi+d)=(η+λi)(qi+d), 将 Aqi=λiqi 代入后整理可得
(ηI−E)(qi+d)=(A−λiI)d. 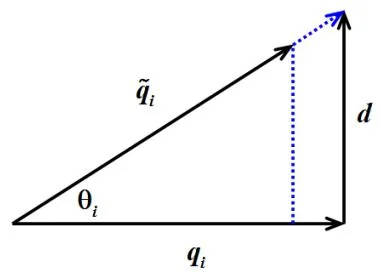
又 qi⊤(A−λiI)=((A−λiI)qi)⊤=0, 故用 qi⊤ 左乘上式两边可得
qiT(ηI−E)(qi+d)=qiT(A−λiI)d=0,(5.17) 即 (ηI−E)(qi+d)∈span{qi}⊥=span{q1,…,qi−1,qi+1,…,qn} . 所以可设 (ηI−E)(qi+d)=∑j=iαjqj . 又 qi⊤d=0 , 故可设 d=∑j=iδjqj . 所以
∑j=iαjqj=(ηI−E)(qi+d)=(A−λiI)d=(A−λiI)∑j=iδjqj=∑j=iδj(A−λiI)qj=∑j=iδj(λj−λi)qj. 由于 q1,q2,…,qn 线性无关,故可得 δj(λj−λi)=αj . 又 gap(λi,A)>0 ,即 j=i 时 λj=λi ,所以 δi=λj−λiαi ,因此
d=j=i∑λj−λiαjqj. 注意到 qi⊤d=0 且 qi⊤qi=1 , 所以由 (\refeq:2) 可得
η=qiTE(qi+d). 故
(ηI−E)(qi+d)=(qi+d)η−E(qi+d)=(qi+d)qi⊤E(qi+d)−E(qi+d)=((qi+d)qiT−I)E(qi+d). 由习题5.5可知 ∥(qi+d)qi⊤−I∥2=∥qi+d∥2 ,故
tanθi=∥d∥2=(∑j=iλj−λiαj2)1/2≤(∑j=igap(λi,A)αj2)1/2=gap(λi,A)1(∑j=iαj2)1/2=gap(λi,A)1∑j=iαjqj2=gap(λi,A)1∥(ηI−E)(qi+d)∥2 ≤gap(λi,A)1∥(qi+d)qi⊤−I∥2⋅∥E∥2⋅∥(qi+d)∥2=gap(λi,A)1∥(qi+d)∥22⋅∥E∥2=gap(λi,A)1⋅cos2θi1∥E∥2. 即
21sin2θi=sinθicosθi=tanθicosθi2≤gap(λi,A)1∥E∥2. 将 A+E 看作原矩阵, (A+E)−E 看作是扰动矩阵, 则可证明第二个结论.

当 θi≪1 时, 21sin2θi≈θi≈sinθi;
若 ∥E∥2≥21gap(λi,A) ,则定理中给出的上界就失去了实际意义;
在该定理中, 没有对特征值进行排序;
在实际计算中, 我们通常所知道的是 gap(λ~i,A+E) .
5.7.4 Rayleigh商逼近
定理5.27 设对称矩阵 A∈Rn×n 的特征值为 λ1,λ2,…,λn
(1) 若 x∈Rn 是单位向量, β∈R , 则
1≤i≤nmin∣λi−β∣≤∥Ax−βx∥2;(5.18) (2) 对于给定的非零向量 x∈Rn , 当 β=ρ(x) 时, ∥Ax−βx∥2 达到最小, 即
β∈Rmin∥Ax−βx∥2=∥Ax−ρ(x)x∥2;(5.19) (3) 令 r=Ax−ρ(x)x , 其中 x∈Rn 为单位向量. 设 λi 是距离 ρ(x) 最近的特征值, gap′=minj=i∣λj−ρ(x)∣ , θ 是 x 和 qi 之间的锐角, 其中 qi 是 λi 对应的单位特征向量, 则
sinθ≤gap′∥r∥2且∣λi−ρ(x)∣≤gap′∥r∥22.(5.20) (留作课外自习)
证明. (1) 若 β 是 A 的特征值, 则结论显然成立
若 β 不是 A 的特征值, 则 A−βI 非奇异, 故
1=∥x∥2=(A−βI)−1(A−βI)x2≤(A−βI)−12⋅∥(A−βI)x∥2.(5.21) 由于 A−βI 对称,且特征值为 λi−β ,故
∥(A−βI)−1∥2=min1≤i≤n∣λi−β∣1. 代入 (\refeq:1) 即可知结论成立
(2) 由于
xT(Ax−ρ(x)x)=xTAx−xTxxTAxxTx=0, 即 x⊥(Ax−ρ(x)x) . 所以
∥Ax−βx∥22=∥(A−ρ(x))x+(ρ(x)−β)x∥22=∥Ax−ρ(x)x∥22+∥(ρ(x)−β)x∥22≥∥Ax−ρ(x)x∥22, 所以当 β=ρ(x) 时, ∥Ax−βx∥2 达到最小
(3) 略

由 (5.11) 可知, 在幂迭代和反迭代中可以使用残量 ∥Ax−λ~x∥2<tol 作为停机准则, 这里 λ~ 是迭代过程中计算得到的近似特征值. 等式 (5.12) 则解释了为什么用 Rayleigh 商来近似特征值.
不等式(5.13)表明 ∣λi−ρ(x)∣ 的值与残量范数 ∥r∥2 的平方成正比,这个结论是Rayleigh商迭代局部三次收敛的基础.
5.7.5 相对扰动分析*
这里主要讨论 A 和 XTAX 的特征值和特征向量之间的扰动关系, 其中 X 非奇异且满足 ∥XTX−I∥2=ε . 这是因为在计算特征向量时, 由于舍入误差的原因, 最后得到的正交矩阵 Q 会带有误差, 从而失去正交性.
定理5.28 (相对Weyl定理) 设对称矩阵 A 和 XTAX 的特征值分别为 λ1≥λ2≥⋯≥λn 和 λ~1≥λ~2≥⋯≥λ~n, 令 ε=∥XTX−I∥2 ,则
∣λ~i−λi∣≤ε∣λi∣或∣λi∣∣λ~i−λi∣≤ε(ifλi=0). (留作课外自习)
证明. 因为 A−λiI 的第 i 个特征值为0, 故由Sylvester惯性定理5.11可知
XT(A−λiI)X=(XTAX−λiI)+λi(I−XTX) 的第 i 个特征值也为0.由Weyl定理5.22可知
(λ~i−λi)−0≤λi(I−XTX)2=ε∣λi∣, 即定理结论成立

当 X 正交时, ε=0 , 故 XTAX 与 A 有相同的特征值. 当 X 几乎正交时, ε 很小, 此时 XTAX 与 A 的特征值几乎相同.
推论5.29设 G 和 YTGX 的奇异值分别为 σ1≥σ2≥⋯≥σn 和 σ~1≥σ~2≥⋯≥σ~n, 令
ε=max{∥XTX−I∥2,∥YTY−I∥2},则 ∣σ~i−σi∣≤ε∣σi∣或∣σi∣∣σ~i−σi∣≤ε(ifσi=0). 下面给出特征向量的相对扰动性质
定义5.4设 A∈Rn×n 的特征值为 λ1,λ2,…,λn ,若 λi=0 ,则 λi 与其余特征值之间的相对间隙(relative gap)定义为
relgap(λi,A)=j=imin∣λi∣∣λj−λi∣. 定理5.30 设 A∈Rn×n 和 X⊤AX∈Rn×n 的特征值分解分别为 A=QΛQ⊤ 和 X⊤AX=Q~Λ~Q~⊤ , 其中 Q=[q1,q2,…,qn] 和 Q~=[q~1,q~2,…,q~n] 均为正交矩阵, Λ=diag(λ1,λ2,…,λn) , Λ~=diag(λ~1,λ~2,…,λ~n) 且 λ1≥λ2≥⋯≥λn , λ~1≥λ~2≥⋯≥λ~n . 设 θi 表示 qi 和 q~i 之间的锐角, 令 ε1=∥I−X−TX−1∥2 , ε2=∥X−I∥2 , 若 ε1<1 且 relgap(λ~i,X⊤AX)>0 , 则
21sin2θi≤1−ε1ε1⋅relgap(λ~i,X⊤AX)1+ε2. (留作课外自习)
证明.设 η=λ~i−λi,H=A−λ~iI,F=λ~i(I−X−TX−1) ,则 Hqi=Aqi−λ~iqi=−ηqi
H+F=A−λ~iX−TX−1=X−T(X⊤AX−λ~iI)X−1. 故 (H+F)(Xq~i)=0. 即 Xq~i 是 H+F 的第 i 个特征值 λ~i=0 的一个特征向量.设 θ1 是 qi 与 Xq~i 之间的锐角,由定理5.26可知
21sin2θ1≤gap(λi,H+F)∥F∥2=gap(λi,H+F)ε1∣λ~i∣.(5.22) 由于 λ~i=0 ,故 gap(λi,H+F) 即为 H+F 的最小非零特征值的绝对值.又 XT(H+F)X=XTAX−λ~iI 的特征值为 λ~j−λ~i,j=1,2,…,n, 且
λ~1−λ~i≥λ~2−λ~i≥⋯≥λ~n−λ~i, 所以由相对Weyl定理5.28可知
λ^j−(λ~j−λ~i)≤ε1λ~j−λ~i. 这里 λ^j 表示 H+F 的第 j 个特征值(按降序排列).因此 ∣λ^j∣≥(1−ε1)∣λ~j−λ~i∣ ,故
gap(λ^i,H+F)≥(1−ε1)gap(λ~i,X⊤AX). 代入 (出) 可得
21sin2θ1≤(1−ε1)gap(λ~i,X⊤AX)ε1∣λ~i∣=1−ε1ε1⋅relgap(λ~i,X⊤AX)1. 设 θ2 是 Xq~i 与 q~i 之间的锐角,则由右图可知
sinθ2=∥q~i∥2sinθ2≤∥Xq~i−q~i∥2≤∥X−I∥2⋅∥q~i∥2=ε2. 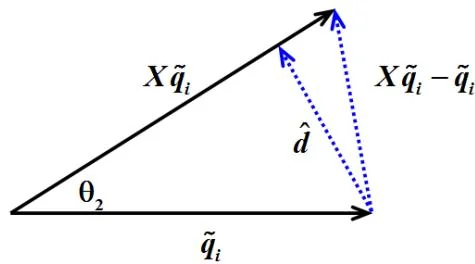
又 θi≤θ1+θ2 ,故
21sin2θi≤21sin2θ1+21sin2θ2≤21sin2θ1+sinθ2≤1−ε1ε1⋅relgap(λ~i,X⊤AX)1+ε2, 即定理结论成立.







