6.1_矩阵分裂与迭代法

6.1 矩阵分裂与迭代法

首先给出矩阵分裂的定义

定义6.1（矩阵分裂Matrix Splitting）设 A∈Rn×nA \in \mathbb{R}^{n \times n} 非奇异，称

A=M−N(6.1)A = M - N \tag {6.1}

为 AA 的一个矩阵分裂, 其中 MM 非奇异.

考虑线性方程组

Ax=b,(6.2)A x = b, \tag {6.2}

其中 A∈Rn×nA \in \mathbb{R}^{n \times n} 非奇异. 迭代法的基本思想: 给定一个迭代初始值 x(0)x^{(0)} , 通过一定的迭代格式生成一个迭代序列 {x(k)}k=0∞\{x^{(k)}\}_{k=0}^{\infty} , 使得

lim⁡k→∞x(k)=x∗≜A−1b.\lim _ {k \to \infty} x ^ {(k)} = x _ {*} \triangleq A ^ {- 1} b.

给定一个矩阵分裂 (6.1), 则原方程组 (6.2) 就等价于 Mx=Nx+bMx = Nx + b . 于是我们就可以构造出以下的迭代格式

Mx(k+1)=Nx(k)+b,k=0,1,2,…,M x ^ {(k + 1)} = N x ^ {(k)} + b, \quad k = 0, 1, 2, \dots ,

或

x(k+1)=M−1Nx(k)+M−1b≜Gx(k)+g,k=0,1,2,…,(6.3)x ^ {(k + 1)} = M ^ {- 1} N x ^ {(k)} + M ^ {- 1} b \triangleq G x ^ {(k)} + g, \quad k = 0, 1, 2, \dots , \tag {6.3}

其中 G≜M−1NG \triangleq M^{-1}N 称为迭代矩阵. 这就是基于矩阵分裂 (6.1) 的迭代法. 易知, 选取不同的 MM , 就可以构造出不同的迭代法.

6.1.1 Jacobi 迭代法

将矩阵 AA 写成

A=D−L−U,A = D - L - U,

其中 DD 为 AA 的对角线部分, −L-L 和 −U-U 分别为 AA 的严格下三角和严格上三角部分.

在矩阵分裂 A=M−NA = M - N 中取 M=D,N=L+UM = D, N = L + U , 则可得 Jacobi 迭代法:

x(k+1)=D−1(L+U)x(k)+D−1b,k=0,1,2,… .(6.4)x ^ {(k + 1)} = D ^ {- 1} (L + U) x ^ {(k)} + D ^ {- 1} b, \quad k = 0, 1, 2, \dots . \tag {6.4}

对应的迭代矩阵为

GJ=D−1(L+U).G _ {\mathrm {J}} = D ^ {- 1} (L + U).

写成分量形式即为

xi(k+1)=1aii(bi−∑j=1,j≠inaijxj(k)),i=1,2,…,n.x _ {i} ^ {(k + 1)} = \frac {1}{a _ {i i}} \left(b _ {i} - \sum_ {j = 1, j \neq i} ^ {n} a _ {i j} x _ {j} ^ {(k)}\right), \quad i = 1, 2, \dots , n.

由于 Jacobi 迭代法中 xi(k+1)x_{i}^{(k + 1)} 的更新顺序与 ii 无关, 即可以按顺序 i=1,2,…,ni = 1,2,\dots ,n 计算, 也可以按顺序 i=n,n−1,…,2,1i = n,n - 1,\ldots ,2,1 计算, 或者乱序计算. 因此 Jacobi 迭代法非常适合并行计算.

算法6.1.Jacobi迭代法

1: Given an initial guess x(0)x^{(0)}
2: while not converge do
3: for i=1i = 1 to nn do

4: xi(k+1)=1aii(bi−∑j=1,j≠inaijxj(k))x_{i}^{(k + 1)} = \frac{1}{a_{ii}}\left(b_{i} - \sum_{j = 1,j\neq i}^{n}a_{ij}x_{j}^{(k)}\right)

5: end for
6: end while

我们有时也将 Jacobi 迭代格式写为

x(k+1)=x(k)+D−1(b−Ax(k))=x(k)+D−1rk,k=0,1,2,…,x ^ {(k + 1)} = x ^ {(k)} + D ^ {- 1} (b - A x ^ {(k)}) = x ^ {(k)} + D ^ {- 1} r _ {k}, \quad k = 0, 1, 2, \dots ,

其中 rk≜b−Ax(k)r_k \triangleq b - A x^{(k)} 是 kk 次迭代后的残量. 这表明, x(k+1)x^{(k+1)} 是通过对 x(k)x^{(k)} 做一个修正得到的.

6.1.2 Gauss-Seidel 迭代法

在分裂 A=M−NA = M - N 中取 M=D−L,N=UM = D - L, N = U , 即可得 Gauss-Seidel (G-S) 迭代法:

x(k+1)=(D−L)−1Ux(k)+(D−L)−1b.(6.5)x ^ {(k + 1)} = (D - L) ^ {- 1} U x ^ {(k)} + (D - L) ^ {- 1} b. \tag {6.5}

对应的迭代矩阵为

GGS=(D−L)−1U.G _ {\mathrm {G S}} = (D - L) ^ {- 1} U.

将G-S迭代法改写为

Dx(k+1)=Lx(k+1)+Ux(k)+b,D x ^ {(k + 1)} = L x ^ {(k + 1)} + U x ^ {(k)} + b,

即可得分量形式

xi(k+1)=1aii(bi−∑j=1i−1aijxj(k+1)−∑j=i+1naijxj(k)),i=1,2,…,n.x _ {i} ^ {(k + 1)} = \frac {1}{a _ {i i}} \left(b _ {i} - \sum_ {j = 1} ^ {i - 1} a _ {i j} x _ {j} ^ {(k + 1)} - \sum_ {j = i + 1} ^ {n} a _ {i j} x _ {j} ^ {(k)}\right), \quad i = 1, 2, \ldots , n.

算法6.2.Gauss-Seidel迭代法

1: Given an initial guess x(0)x^{(0)}
2: while not converge do
3: for i=1i = 1 to nn do

4: xi(k+1)=1aii(bi−∑j=1i−1aijxj(k+1)−∑j=i+1naijxj(k))x_{i}^{(k + 1)} = \frac{1}{a_{ii}}\left(b_{i} - \sum_{j = 1}^{i - 1}a_{ij}x_{j}^{(k + 1)} - \sum_{j = i + 1}^{n}a_{ij}x_{j}^{(k)}\right)

5: end for
6: end while

A G-S 迭代法的主要优点是充分利用了已经获得的最新数据.
Δ\Delta 但在G-S迭代法中, 未知量的更新必须按自然顺序进行, 因此不适合并行计算.

6.1.3 SOR迭代法

在 G-S 迭代法的基础上, 我们可以通过引入一个松弛参数 ω\omega 来加快收敛速度. 这就是 SOR (Successive Overrelaxation) 方法 [140]. 该方法的基本思想是将 G-S 迭代法中的第 k+1k + 1 步近似解与第 kk 步近似解做一个加权平均, 从而给出一个新的近似解, 即

x(k+1)=(1−ω)x(k)+ωD−1(Lx(k+1)+Ux(k)+b).(6.6)x ^ {(k + 1)} = (1 - \omega) x ^ {(k)} + \omega D ^ {- 1} \left(L x ^ {(k + 1)} + U x ^ {(k)} + b\right). \tag {6.6}

整理后即为

x(k+1)=(D−ωL)−1((1−ω)D+ωU)x(k)+ω(D−ωL)−1b,x ^ {(k + 1)} = (D - \omega L) ^ {- 1} \big ((1 - \omega) D + \omega U \big) x ^ {(k)} + \omega (D - \omega L) ^ {- 1} b,

其中 ω\omega 称为松弛参数(relaxation parameter).

  • 当 ω=1\omega = 1 时, SOR 即为 G-S 迭代法,

  • 当 ω<1\omega < 1 时, 称为低松弛 (under relaxation) 迭代法,

  • 当 ω>1\omega > 1 时, 称为超松弛 (over relaxation) 迭代法.

在大多数情况下, 当 ω>1\omega > 1 时会取得比较好的收敛效果.

SOR迭代法曾经在很长一段时间内是科学计算中求解线性方程组的首选方法.

SOR的迭代矩阵为

GS O R=(D−ωL)−1((1−ω)D+ωU),G _ {\text {S O R}} = (D - \omega L) ^ {- 1} ((1 - \omega) D + \omega U),

对应的矩阵分裂为

M=1ωD−L,N=1−ωωD+U.M = \frac {1}{\omega} D - L, \quad N = \frac {1 - \omega}{\omega} D + U.

由 (6.6) 可知 SOR 迭代法的分量形式为

xi(k+1)=(1−ω)xi(k)+ωaii(bi−∑j=1i−1aijxj(k+1)−∑j=i+1naijxj(k))=xi(k)+ωaii(bi−∑j=1i−1aijxj(k+1)−∑j=inaijxj(k))\begin{array}{l} x _ {i} ^ {(k + 1)} = (1 - \omega) x _ {i} ^ {(k)} + \frac {\omega}{a _ {i i}} \left(b _ {i} - \sum_ {j = 1} ^ {i - 1} a _ {i j} x _ {j} ^ {(k + 1)} - \sum_ {j = i + 1} ^ {n} a _ {i j} x _ {j} ^ {(k)}\right) \\ = x _ {i} ^ {(k)} + \frac {\omega}{a _ {i i}} \left(b _ {i} - \sum_ {j = 1} ^ {i - 1} a _ {i j} x _ {j} ^ {(k + 1)} - \sum_ {j = i} ^ {n} a _ {i j} x _ {j} ^ {(k)}\right) \\ \end{array}

算法6.3. 求解线性方程组的SOR迭代法

1: Given an initial guess x(0)x^{(0)} and parameter ω\omega
2: while not converge do
3: for i=1i = 1 to nn do

4: xi(k+1)=(1−ω)xi(k)+ωaii(bi−∑j=1i−1aijxj(k+1)−∑j=i+1naijxj(k))x_{i}^{(k + 1)} = (1 - \omega)x_{i}^{(k)} + \frac{\omega}{a_{ii}}\left(b_{i} - \sum_{j = 1}^{i - 1}a_{ij}x_{j}^{(k + 1)} - \sum_{j = i + 1}^{n}a_{ij}x_{j}^{(k)}\right)
5: end for
6: end while

SOR 迭代法最大的优点是引入了松弛参数 ω\omega : 通过选取适当的 ω\omega 就可以大大提高方法的收敛速度. 但是 SOR 迭代法最大的难点就是如何选取最优的参数.

6.1.4 SSOR 迭代法

将SOR迭代法中的 LL 和 UU 相互交换位置, 则可得迭代格式

x(k+1)=(D−ωU)−1((1−ω)D+ωL)x(k)+ω(D−ωU)−1b.x ^ {(k + 1)} = (D - \omega U) ^ {- 1} ((1 - \omega) D + \omega L) x ^ {(k)} + \omega (D - \omega U) ^ {- 1} b.

将这个迭代格式与SOR相结合，就可以得到下面的两步迭代法

{x(k+12)=(D−ωL)−1[(1−ω)D+ωU]x(k)+ω(D−ωL)−1b,x(k+1)=(D−ωU)−1[(1−ω)D+ωL]x(k+12)+ω(D−ωU)−1b.\left\{ \begin{array}{l} x ^ {(k + \frac {1}{2})} = (D - \omega L) ^ {- 1} \big [ (1 - \omega) D + \omega U \big ] x ^ {(k)} + \omega (D - \omega L) ^ {- 1} b, \\ x ^ {(k + 1)} = (D - \omega U) ^ {- 1} \big [ (1 - \omega) D + \omega L \big ] x ^ {(k + \frac {1}{2})} + \omega (D - \omega U) ^ {- 1} b. \end{array} \right.

这就是对称超松弛(SSOR)迭代法,相当于将 LL 与 UU 同等看待，交替做两次SOR迭代法.

消去中间迭代向量 x(k+12)x^{(k + \frac{1}{2})} ，可得

x(k+1)=GSSORx(k)+g,x ^ {(k + 1)} = G _ {\mathrm {S S O R}} x ^ {(k)} + g,

其中迭代矩阵

GSSOR=(D−ωU)−1[(1−ω)D+ωL](D−ωL)−1[(1−ω)D+ωU].G _ {\mathrm {S S O R}} = (D - \omega U) ^ {- 1} \bigl [ (1 - \omega) D + \omega L \bigr ] (D - \omega L) ^ {- 1} \bigl [ (1 - \omega) D + \omega U \bigr ].

对应的矩阵分裂为

M=1ω(2−ω)[D−ω(L+U)+ω2LD−1U]=1ω(2−ω)(D−ωL)D−1(D−ωU),\begin{array}{l} M = \frac {1}{\omega (2 - \omega)} \big [ D - \omega (L + U) + \omega^ {2} L D ^ {- 1} U \big ] \\ = \frac {1}{\omega (2 - \omega)} (D - \omega L) D ^ {- 1} (D - \omega U), \\ \end{array}
N=1ω(2−ω)[(1−ω)D+ωL]D−1[(1−ω)D+ωU].N = \frac {1}{\omega (2 - \omega)} \bigl [ (1 - \omega) D + \omega L \bigr ] D ^ {- 1} \bigl [ (1 - \omega) D + \omega U \bigr ].

对于某些特殊问题, SOR 迭代法不收敛, 但仍然可能构造出收敛的 SSOR 迭代法.
一般来说,SOR收敛速度要快于SSOR,但SOR的收敛速度对参数 ω\omega 更敏感.

算法6.4. SSOR迭代法

1: Given an initial guess v(0)v^{(0)} and parameter ω\omega
2: while not converge do
3: for i=1i = 1 to nn do

4:

xi(k+12)=(1−ω)xi(k)+ωaii(bi−∑j=1i−1aijxj(k+12)−∑j=i+1naijxj(k))x _ {i} ^ {(k + \frac {1}{2})} = (1 - \omega) x _ {i} ^ {(k)} + \frac {\omega}{a _ {i i}} \left(b _ {i} - \sum_ {j = 1} ^ {i - 1} a _ {i j} x _ {j} ^ {(k + \frac {1}{2})} - \sum_ {j = i + 1} ^ {n} a _ {i j} x _ {j} ^ {(k)}\right)

5:

endfore n d \mathrm {f o r}

6:

fori=nt o1do\mathbf {f o r} i = n \text {t o} 1 \mathbf {d o}
xi(k+1)=(1−ω)xi(k+12)+ωaii(bi−∑j=1i−1aijxj(k+12)−∑j=i+1naijxj(k+1))x _ {i} ^ {(k + 1)} = (1 - \omega) x _ {i} ^ {(k + \frac {1}{2})} + \frac {\omega}{a _ {i i}} \left(b _ {i} - \sum_ {j = 1} ^ {i - 1} a _ {i j} x _ {j} ^ {(k + \frac {1}{2})} - \sum_ {j = i + 1} ^ {n} a _ {i j} x _ {j} ^ {(k + 1)}\right)

8:

endfore n d \mathrm {f o r}

9:

lwhilel \mathrm {w h i l e}

6.1.5 AOR迭代法*

Hadjidimos于1978年提出了加速超松弛(Accelerated Over-Relaxation, AOR)迭代法，迭代矩阵为

GAOR=(D−γL)−1[(1−ω)D+(ω−γ)L+ωU],G _ {\mathrm {A O R}} = (D - \gamma L) ^ {- 1} \left[ (1 - \omega) D + (\omega - \gamma) L + \omega U \right],

其中 γ\gamma 和 ω\omega 为松弛参数. 对应的矩阵分裂为

M=1ω(D−γL),N=1ω[(1−ω)D+(ω−γ)L+ωU].M = \frac {1}{\omega} (D - \gamma L), \quad N = \frac {1}{\omega} [ (1 - \omega) D + (\omega - \gamma) L + \omega U ].

易知:

(1) 当 γ=ω\gamma = \omega 时, AOR 即为 SOR 迭代法;
(2) 当 γ=ω=1\gamma = \omega = 1 时, AOR 即为 G-S 迭代法;
(3) 当 γ=0,ω=1\gamma = 0, \omega = 1 时，AOR 即为 Jacobi 迭代法

AOR迭代法中含有两个参数.因此在理论上，通过选取合适的参数,AOR迭代法会收敛得更快.但也是因为含有两个参数,使得参数的选取变得更加困难,因此较少使用.

与SSOR类似，我们也可以定义SAOR迭代法

6.1.6 Richardson迭代法

Richardson迭代法是一类形式非常简单的算法,其迭代格式为

x(k+1)=x(k)+ω(b−Ax(k)),k=0,1,2,… .x ^ {(k + 1)} = x ^ {(k)} + \omega (b - A x ^ {(k)}), \quad k = 0, 1, 2, \dots .

它可以看作是基于以下矩阵分裂的迭代法：

M=1ωI,N=1ωI−A.M = \frac {1}{\omega} I, \quad N = \frac {1}{\omega} I - A.

对应的迭代矩阵为

GR=I−ωA.G _ {\mathrm {R}} = I - \omega A.

在每次迭代时可以选取不同的参数, 即

x(k+1)=x(k)+ωk(b−Ax(k)),k=0,1,2,… .x ^ {(k + 1)} = x ^ {(k)} + \omega_ {k} (b - A x ^ {(k)}), \quad k = 0, 1, 2, \dots .

6.1.7 分块迭代法

如果 AA 的对角线中出现零, 则 Jacobi, G-S, SOR 等方法就不再有定义. 此时我们可以采用分块迭代格式. 另外, 分块迭代法也能提升算法的计算效率.

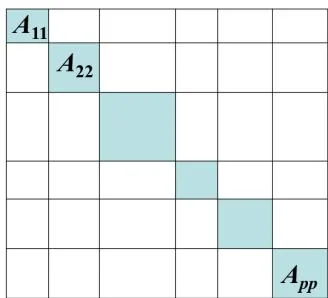
将 AA 写成如下的分块形式(如右图所示)：

A=[A11A12…A1pA21A22…A2p⋮⋮⋱⋮Ap1Ap2…App],A = \left[ \begin{array}{c c c c} A _ {1 1} & A _ {1 2} & \dots & A _ {1 p} \\ A _ {2 1} & A _ {2 2} & \dots & A _ {2 p} \\ \vdots & \vdots & \ddots & \vdots \\ A _ {p 1} & A _ {p 2} & \dots & A _ {p p} \end{array} \right],

则相应的分块 Jacobi, 分块 G-S 和分块 SOR 迭代法分别定义为:

  • 分块 Jacobi 迭代:

Aiixi(k+1)=bi−∑j=1,j≠ipAijxj(k),i=1,2,…,p.A _ {i i} \boldsymbol {x} _ {i} ^ {(k + 1)} = \boldsymbol {b} _ {i} - \sum_ {j = 1, j \neq i} ^ {p} A _ {i j} \boldsymbol {x} _ {j} ^ {(k)}, \quad i = 1, 2, \dots , p.

  • 分块 Gauss-seidel 迭代:

Aiixi(k+1)=bi−∑j=1i−1Aijxj(k+1)−∑j=i+1pAijxj(k),i=1,2,…,p.A _ {i i} \boldsymbol {x} _ {i} ^ {(k + 1)} = \boldsymbol {b} _ {i} - \sum_ {j = 1} ^ {i - 1} A _ {i j} \boldsymbol {x} _ {j} ^ {(k + 1)} - \sum_ {j = i + 1} ^ {p} A _ {i j} \boldsymbol {x} _ {j} ^ {(k)}, \quad i = 1, 2, \dots , p.

  • 分块SOR迭代：

xi(k+1)=(1−ω)xi(k)+ωAii−1(bi−∑j=1i−1Aijxj(k+1)−∑j=i+1pAijxj(k)),\boldsymbol {x} _ {i} ^ {(k + 1)} = (1 - \omega) \boldsymbol {x} _ {i} ^ {(k)} + \omega A _ {i i} ^ {- 1} \left(\boldsymbol {b} _ {i} - \sum_ {j = 1} ^ {i - 1} A _ {i j} \boldsymbol {x} _ {j} ^ {(k + 1)} - \sum_ {j = i + 1} ^ {p} A _ {i j} \boldsymbol {x} _ {j} ^ {(k)}\right),
i=1,2,…,p.i = 1, 2, \dots , p.

4 分块迭代法采用更多的 3 级 BLAS 运算, 因此更有利于发挥现代计算机的性能.

Previous06_第六讲_线性方程组基本迭代法
Next6.2_收敛性分析