28.1_Rosenbrock 函数
28.1 Rosenbrock函数
本步骤将处理Rosenbrock函数。该函数的式子如下,其形状如图28-1所示。
观察图28-1,可以看到函数像是一个抛物线形状的绵延不断的山谷。如果画出图28-1中“山”的等高线,就会发现线的形状很像香蕉,所以Rosenbrock函数也叫“香蕉函数”。
本步骤的目标是找到使Rosenbrock函数的输出值最小的 和 。先说答案,Rosenbrock函数的最小值在 处。在本步骤,我们将使用DeZero,看看它能否真的找到这个最小值。
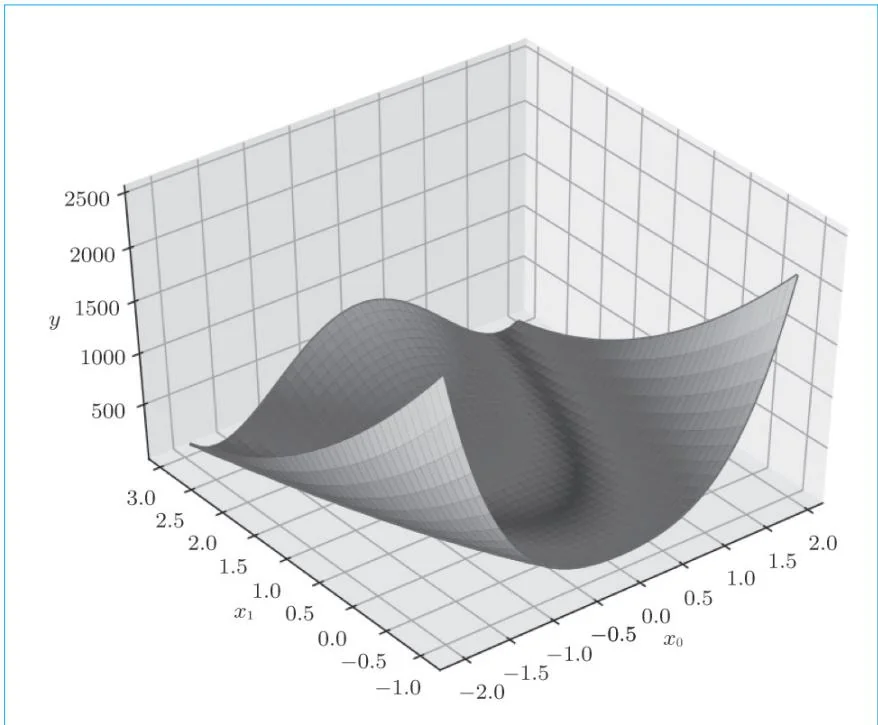
图28-1 Rosenbrock函数的形状(图片引自参考文献[19])

Rosenbrock函数的严格的定义是 ,其中 和 是常数。上面的例子是 、 时的 Rosenbrock 函数。Rosenbrock 函数常作为优化问题的基准函数来使用。当 Rosenbrock 函数作为基准函数时,一般使用 、 作为 和 的值。