57.2_conv2d函数的实现
57.2 conv2d函数的实现
本书把DeZero的im2col函数当作黑盒使用(不关注其内部实现)。im2col函数是对Variable实例的输入进行计算的DeZero函数,其导数可以通过backward求得。

由于CNN的函数代码较多,所以我们不将CNN相关的代码保存在dezero/functions.py中,而是保存在dezero/functions_conv.py中。DeZero的im2col函数也在dezero/functions_conv.py中。另外,dezero/functions.py中导入了dezero/functions_conv.py中实现的DeZero函数。这样用户就能从dezero/functions.py导入所有的函数。
现在来看DeZero的im2col函数,它有以下参数。表57-1是对其参数的说明。
im2col(x, kernel_size, stride=1, pad=0, to_matrix=True)表 57-1 im2col 函数的参数
kernel_size参数可以是int或(int,int)(元组)。如果传来的值是(int,int),那么第一个元素对应于高度,第二个元素对应于宽度;如果只传int,那么高度和宽度是同一个值。参数stride和pad的类型也一样。最后的参数to_matrix是标志位,如果为True,则指示函数在取出应用卷积核的区域后将其变为矩阵(这样就能以矩阵的乘积进行计算了)。
下面来实际使用这个im2col函数。
steps/step57.py
import numpy as np
importdezero-functionsasF
$\mathrm{x1} = \mathrm{np.random.randint(1,3,7,7)}$
col1 $=$ F.im2col(x1,kernel_size=5,stride $= 1$ pad $= 0$ to_matrix=True) print(col1.shape)dezero/util.py
$\texttt{x2} = \texttt{np.random.randint(10,3,7,7)}$ #10个数据
kernel_size $= (5,5)$
stride $= (1,1)$
pad $= (\theta ,\theta)$
col2 $= \mathrm{F.im2col(x2}$ ,kernel_size,stride,pad,to_matrix $\equiv$ True)
print(col2.shape)运行结果
(9,75) (90,75)上面的代码展示了两个例子。第一个是形状为 的数据,即数据的批量大小为1,通道数为3,高为7,宽为7。第二个例子是将第一个例子的批量大小增加到10的情况。分别对两个数据集应用im2col函数后,第二维的元素数都变为75。这与卷积核的元素数(通道数为3,大小为 )一致。另外,批量大小为1的im2col的结果大小为(9,75)。第二个例子的批量大小为10,所以结果大小为(90,75),是第一个例子的10倍。
接下来使用im2col函数来实现进行卷积运算的DeZero的函数。在此之前,首先实现工具函数pair(x)。
def pair(x):
if isinstance(x, int):
return (x, x)
elif isinstance(x, tuple):
assert len(x) == 2
return x
else:
raise ValueError如果参数 是 int, 函数 pair(x) 将返回 (x, x)。如果 是有两个元素的元组, pair(x) 则将其按原样返回。在使用这个函数的情况下, 不管输入是 int 还是 (int, int), 我们都可以得到具有两个元素的元组。示例如下所示。
fromdezero.utilismportpair
print pair(1))
print (pair((1,2)))运行结果
(1, 1)
(1, 2)
下面实现进行卷积运算的函数 conv2d simples(将以下代码添加到dezero/functions_conv.py,而不是dezero/functions.py中)。
dezero/functions_conv.py
fromdezero.utilisimportpair,get_conv_outsize
def conv2d.simple(x,W,b=None,stride $\coloneqq 1$ pad $= 0$ : x,W $=$ as_variable(x),as_variable(W) Weight $=$ W #为了避免WWidth和Weight)冲突 N,C,H,W=x.shape OC,C,KH,KW $=$ Weight.shape SH,SW $=$ pair(stride) PH,PW $=$ pairPAD OH $=$ get_conv_outsize(H,KH,SH,PH) OW $=$ get_conv_outsize(W,KW,SW,PH) col $=$ im2col(x,(KH,KW),stride,pad,to_matrix=True)# $①$ Weight $=$ Weight.reshape(OC,-1).transpose() # $②$ t $=$ linear(col,Weight,b)# $③$ y $=$ t.reshape(N,OH,OW,OC).transpose(0,3,1,2) # $④$ returny上面代码中重要的部分用阴影表示。①处使用im2col展开输入数据,②处将卷积核(Weight)像图57-2那样并排展开为一列。通过在Weight.reshape(OC, -1)中指定-1可以做到这一点,这是reshape函数的一个便利的功能。如果reshape函数的参数被指定为-1,在保持多维数组元素数量不变的情况下,元素会被降维合并到一起。例如,形状为(10,3,5,5)的数组的元素数是750,对这个数组使用reshape(10,-1),它将变换为形状是(10,75)的数组。
③处计算矩阵的乘积,这一行使用了用于线性变换的linear函数进行包含偏置的计算。最后的④处将输出变换为合适的形状。在变换时使用了DeZero的transpose函数。步骤38中曾经介绍过transpose函数可以用来交换张量的轴的顺序,这里我们以图57-3的形式改变轴的顺序。
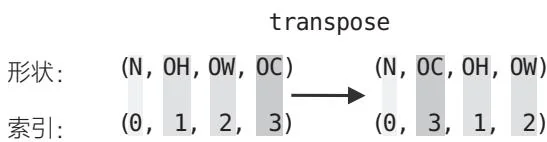
图57-3 通过transpose函数交换轴的顺序
以上就是conv2d.simple函数的实现。由于我们在实现卷积运算时使用的是此前实现的DeZero函数,所以它的反向传播也可以正确进行。例如,我们可以按以下方式使用conv2d.simple函数。
steps/step57.py
N, C, H, W = 1, 5, 15, 15
OC, (KH, Kw) = 8, (3, 3)
x = Variable(np.random.randint(N, C, H, W))
W = np.random.randint(OC, C, KH, Kw)
y = F.conv2d.simple(x, W, b=None, stride=1, pad=1)
y.backup()
print(y.shape)
print(x.grad.shape)运行结果
(1,8,15,15) (1,5,15,15)上面的代码成功地执行了卷积运算。这里展示的卷积运算采用了普通的实现方式(因此函数也被命名为conv2d.simple),更好的实现方式是实现继承Function类的Conv2d类。Conv2d类和conv2d函数的代码在dezero/functions_conv.py中。感兴趣的读者可以查阅。

Conv2d类在正向传播阶段使用im2col方法,并通过张量积进行计算。另外,通过im2col展开的二阶张量(这里称之为col)在使用后会立即从内存中删除(因为col非常大,会占用很多内存)。之后的反向传播阶段通过转置卷积①来进行计算。