22.2 减法

减法式子 $y = x_{0} - x_{1}$ 的导数为 $\frac{\partial y}{\partial x_0} = 1$ 和 $\frac{\partial y}{\partial x_1} = -1$ 。因此，在反向传播时，针对从上游传来的导数，把乘以1得到的结果作为 $x_{0}$ 的导数，把乘以-1得到的结果作为 $x_{1}$ 的导数。在此基础上编写的代码如下所示。

steps/step22.py   
class Sub(Function): def forward(self, x0, x1): y = x0 - x1 return y def backward(self, gy): return gy, -gy   
def sub(x0, x1): x1 = as_array(x1) return Sub()  $(x0,x1)$    
Variable._sub_  $=$  sub

如果 $x0$ 和 $x1$ 是Variable实例，就可以执行 $y = x0 - x1$ 的计算了。但是，如果 $x0$ 不是Variable实例，就无法正确执行 $y = 2.0 - x$ 这样的计算。在这种情况下被调用的是 $x$ 的__rsub__方法，参数以图22-1的方式传递。

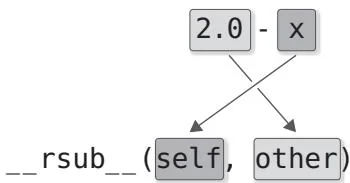
图22-1 向__rsub__方法传递参数的示意图

如图22-1所示，在调用__rsub__(self, other)时，减号运算符右项的x传给了self参数。考虑到这一点，__rsub__应按如下方式实现。

steps/step22.py

def rsub(x0, x1):
    x1 = as_array(x1)
    return Sub() (x1, x0) # 交换x1和x0
Variable._rsub_ = rsub

上面的代码准备了函数rsub(x0，x1)，函数内部交换了 $x_0$ 和 $x_1$ 的顺序，然后调用了Sub()（x1，x0）。最后函数rsub被赋给特殊方法__rsub__。

在加法运算和乘法运算中，左项和右项交换并不会影响计算结果，所以我们不必区分左右项，但在减法运算的情况下，就要区分左项和右项了（ $\times 0$ 减去 $x1$ 和 $x1$ 减去 $x0$ 的结果是不同的）。因此，我们需要按照前面的方式为右项单独准备一个函数 $\operatorname{rsub}(x0, x1)$ 。

到这里就完成了减法运算的实现，现在我们可以编写以下代码了。

steps/step22.py

$\mathbf{x} =$  Variable(np.array(2.0))  
y1  $= 2.0 - x$    
y2  $= x - 1.0$    
print(y1)  
print(y2)

运行结果

variable(0.0)  
variable(1.0)

接下来是除法运算。