60.2 LSTM层的实现

接下来是第二项改进。这里我们会实现LSTM层，并用它来代替RNN层。下面用式子来表示LSTM所做的计算。

上面的式子是LSTM所做的计算。LSTM除了使用隐藏状态 $\pmb{h}$ ，还使用记忆单元 $\pmb{c}$ 。式子60.2和式子60.3中的 $\odot$ 是哈达玛积的符号，表示每对相应元素的乘积。对式子的介绍到此为止，下面我们在DeZero中实现上面的式子。

本书只介绍 LSTM 的主要内容，更详细的说明请参考本书前作《深度学习进阶：自然语言处理》第 6 章的内容。

下面在DeZero中实现式子60.1、式子60.2和式子60.3。代码如下所示。

dezero/layers.py

class LSTM(Layer): def __init__(self, hidden_size, in_size=None): super().__init__() H, I = hidden_size, in_size self.x2f = Linear(H, in_size=I) self.x2i = Linear(H, in_size=I) self.x2o = Linear(H, in_size=I) self.x2u = Linear(H, in_size=I) self.h2f = Linear(H, in_size=H, nobias=self) self.h2i = Linear(H, in_size=H, nobias=self) self.h2o = Linear(H, in_size=H, nobias=self) self.h2u = Linear(H, in_size=H, nobias=self) self.reset_state() def reset_state(self): self.h = None self.c = None def forward(self, x): if self.h is None: f = F.sigmoid(self.x2f(x)) i = F.sigmoid(self.x2i(x)) o = F.sigmoid(self.x2o(x)) u = F.tanh(self.x2u(x)) else: f = F.sigmoid(self.x2f(x) + self.h2f(self.h)) i = F.sigmoid(self.x2i(x) + self.h2i(self.h)) o = F.sigmoid(self.x2o(x) + self.h2o(self.h)) u = F.tanh(self.x2u(x) + self.h2u(self.h)) if self.c is None: c_new = (i * u) else: c_new = (f * self.c) + (i * u) h_new = o * F.tanh(c_new) self.h, self.c = h_new, c_new return h_new

上面的代码虽然有点多，但主要的工作是将LSTM的式子转换为代码。有了DeZero，即使是LSTM的复杂式子也可以轻松实现。最后再次尝试训练上一个步骤的正弦波。训练代码如下所示。

steps/step60.py

import numpy as np   
importdezero   
fromdezero import Model   
fromdezero import SeqDataLoader   
importdezero-functions as F   
importdezero.layers as L   
max_epoch  $= 100$    
batch_size  $= 30$    
hidden_size  $= 100$    
bptt_length  $= 30$    
train_set  $\equiv$ dezero.datasets.SinCurve(train=True)   
#①使用时间序列数据的数据加载器   
dataloder  $\equiv$  SeqDataLoader(train_set，batch_size  $\equiv$  batch_size)   
seqlen  $\equiv$  len(train_set)   
class BetterRNN(Model): def__init__(self, hidden_size,out_size): super().__init_(） self.rnn  $=$  L.LSTM(hidden_size)#②使用LSTM self.fc  $=$  L.Linear(out_size) def reset_state(self): self.rnn.reset_state() def forward(self,x): y  $=$  self.rnn(x) y  $=$  self.fc(y) returny   
model  $\equiv$  BetterRNN(hidden_size,1) optimizer  $\equiv$ dezero.trainers.Adam().setup(model)   
for epoch in range(max_epoch): model.reset_state() loss，count  $= 0$  ，0 forx,t in dataloader: y  $=$  model(x) loss  $+ =$  F.mean_squared_error(y,t) count  $+ = 1$  if count%bptt_length  $= = 0$  or count  $= =$  seqlen: #dezero.utils.plotDOT_graph(loss）#绘制计算图

model.cleargrades() loss.backup() loss.unchain_backward() optimizer.update() avg_loss  $=$  float(loss.data)/count print('| epoch %d | loss  $\% f^{\prime}\%$  (epoch  $+1$  ,avg_loss))

只有两处与上一个步骤不同。第一处是使用SeqDataLoader类创建数据加载器；第二处是使用LSTM层设计模型。以这种方式进行训练，训练速度会比上一个步骤的更快。现在使用训练好的模型来对新的数据(无噪音的余弦波)进行预测。结果如图60-1所示。

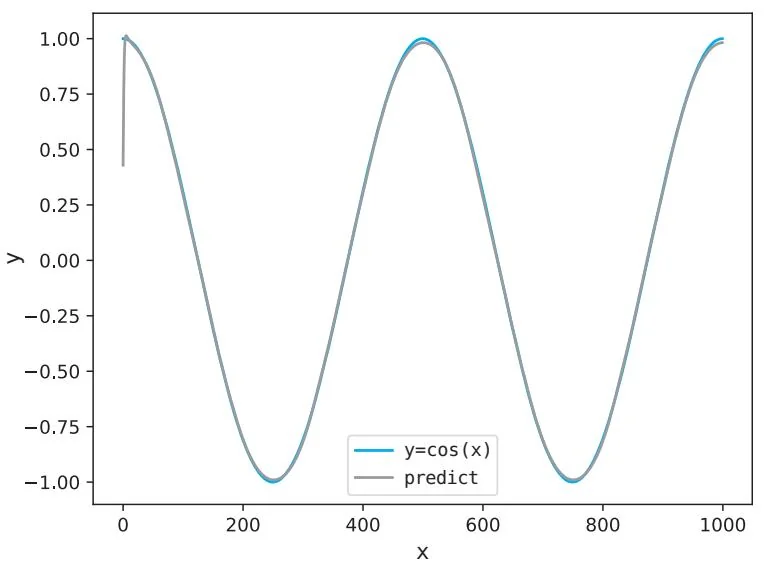
图60-1 使用了LSTM层的模型的预测结果

图60-1表明预测结果良好，比上一个步骤的结果(图59-7)的精度更高。我们已经成功实现了LSTM这种复杂的层，并完成了时间序列数据处理这一复杂任务。最后一起来看一下由前面的代码创建的计算图，计算图如图60-2所示。

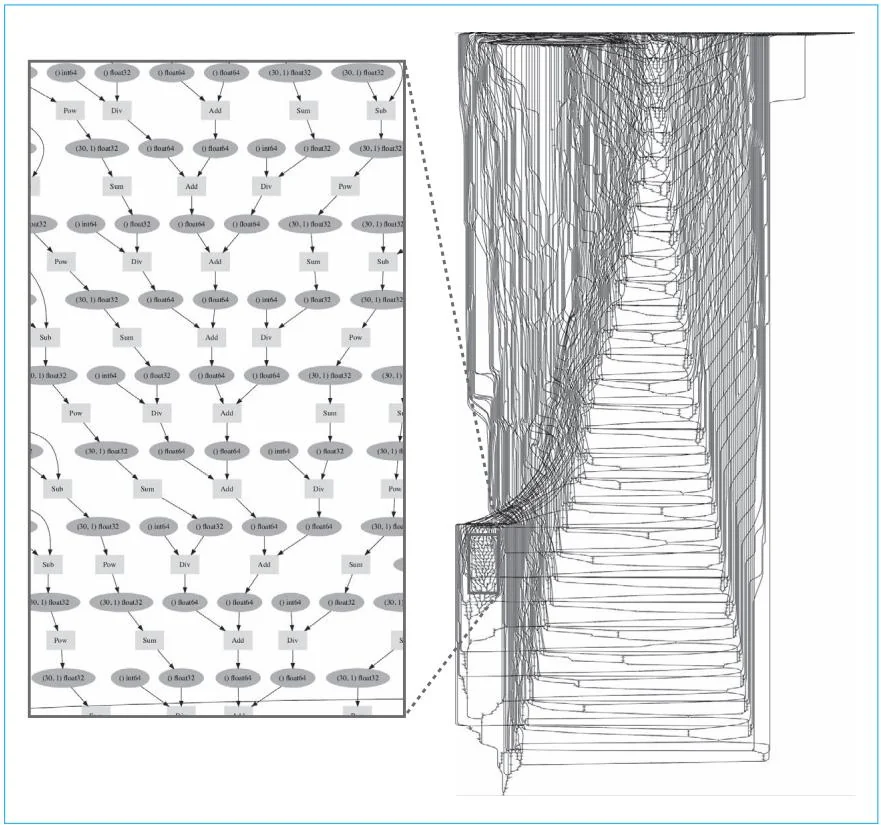
图60-2 使用LSTM模型训练时间序列数据时创建的计算图

如图60-2所示，这里创建的是一个相当复杂的计算图。如果没有DeZero这样的框架，我们很难创建如此复杂的计算图。DeZero的灵活性使得这样一个复杂的计算图的创建工作变得异常简单。不管将来碰到多么复杂的计算，DeZero都可以轻松解决。

本书的60个步骤到此就全部结束了。到达此处意味着我们已经实现了创建深度学习框架的宏伟目标。感谢大家跟随我的脚步走完了这个漫长的旅

程。作为本书的作者，我很开心大家能花这么多时间读完这么多页的内容。

回顾这段旅程，DeZero从最开始的一只小小的“箱子”起步，一点点地扩展，在我们解决各种问题，进行各种实验的同时，DeZero也在不断成长。经过一点点的积累，DeZero已经成长为一个优秀的深度学习框架。现在的DeZero已经具备了许多现代框架应该具备的功能。

虽然本书到此结束，但我们还有很多工作要做。请大家继续走下去，自由地走下去。无论是使用从本书获得的知识来创建自己的原创框架，还是进一步扩展 DeZero，或是改用 PyTorch 或 TensorFlow 等框架，请尽情享受新的旅程。后面的专栏探讨了 DeZero 未来的发展方向，感兴趣的读者可以参考。

专栏：走向未来

本专栏会介绍几个未来针对DeZero可做的工作，其中总结了笔者想到的一些内容，如将来如何扩展DeZero，作为OSS(开源软件)如何进行开发，需要哪些材料等。此外，本专栏还列举了正文中没有提到的DeZero开发过程中的故事（如图标的创作）等。

增加函数和层

本书实现了许多DeZero的函数和层。当然，还有一些函数和层尚未实现。例如，进行张量积计算的tensorDot函数和用于批量正则化的batchNorm函数等。另外，与其他深度学习框架比较一下，我们也会发现还有哪些函数和层尚未实现。例如，通过阅读PyTorch的文档，可以整理出DeZero中缺少的函数。

提高内存的使用效率

提高深度学习框架的内存效率是一个重要的课题，尤其是在大型网络中，由于网络会使用大量的内存，所以深度学习框架经常会出现物理内存不足的问题。在内存的使用效率方面，我们还可以对DeZero做一些改进。最重要的改进是让DeZero保留所有正向传播计算的结果(数据的ndarray实例)，也就是预想反向传播的计算要用到这些结果，在DeZero中保留所有中间计算的结果。但是有些函数不需要保留中间计算的结果。例如tanh函数就能在没有正向传播输入的情况下计算反向传播，因此，在这种情况下，正向传播的输入数据应被立即删除。考虑到这一点，我们可以设计一种机制，根据函数来决定要保留的数据。Chainer和PyTorch其实已经实现了这一机制。感兴趣的读者可以参考Chainer的Aggressive Buffer Release(参考文献[24])等。

静态计算图与ONNX

DeZero采用Define-by-Run(动态计算图)的方式创建计算图，不提供Define-and-Run(静态计算图)的方式。静态计算图适用于对性能有要求的场景，而且静态计算图在经过编译(转换)后，可以在非Python的环境中运行。考虑到这些，或许有些用户希望DeZero也能够运行静态计算图。

另外，在深度学习领域，还有一种叫作ONNX(参考文献[40])的数据格式。ONNX是用来表示深度学习模型的格式，许多框架支持该格式。ONNX的优势在于训练好的模型可以轻松移植到其他框架。如果DeZero也支持ONNX，它就可以与各种框架联动，通用性会更强。

发布到PyPI

软件开发结束之后，为了让用户使用，我们需要将代码汇总成包发布。在Python领域，常用的软件库是PyPI(Python Package Index)。软件包发布到PyPI后，用户就可以使用pip install ...命令来安装软件包，这样任何人都可以轻松使用它。

DeZero已经发布到PyPI了。网上有很多介绍如何将代码发布到PyPI的文章，大家可自行参考。笔者也欢迎大家基于本书的DeZero开发自己的原创框架，并发布到网上供世人使用。有机会请试一试。

准备文档

在发布框架(或库)时，提供文档会方便用户使用。许多有名的框架提供了关于如何使用其函数、类等(API)的文档。

Python 提供了 docstring(文档字符串)方案。docstring 是为 Python 函数或类等编写的说明文字(注释)，需要以固定格式编写在代码中。

DeZero 的实际代码中也有写好的 docstring。例如dezero/cuda.py 中 as_cupy 函数的代码，具体如下所示。

def as_cupy(x):
    '''Convert to `copy.ndarray`.  
Args:
    x ('numpy.ndarray' or 'copy.ndarray'): Arbitrary object that can be converted to `copy.ndarray`.  
Returns:
    'copy.ndarray': Converted array.  
'''if isinstance(x, Variable):
    x = x.data  
if not gpu_enable:
    raise Exception('CuPy cannot be loaded. Install CuPy!')  
return cp.asarray(x)

上面代码中的注释部分包含了函数的基本信息、参数类型、返回值类型等的说明。说明风格有NumPy风格和Google风格等几种比较有名的风格。DeZero采用了Google风格。上面的说明能帮助读者理解函数。当然，这些说明也可以用母语来写(考虑到本书可能会被翻译为多种语言，所以笔者在DeZero中用英语写了docstring)。另外，写好docstring后，可以通过Sphinx(参考文献[39])工具等将其输出为HTML、PDF等形式。在使用Sphinx的情况下，我们可以不费吹灰之力创建出一个专用页面。

制作图标

创建OSS时，我们也可以考虑为它制作一个图标。拥有一个有吸引力的图标有助于得到用户的认可。当然，图标可以由开发者自己制作，但要想使设计更有吸引力，不妨考虑请专业人士来制作。DeZero的图标也是在众包网站上以竞标的形式请人制作的。非常感谢设计者的完美设计。

增加实现示例（examples）

前面介绍的是创建DeZero的过程，而真正有趣的是使用创建的DeZero来

实现有名的研究成果或自己设计的新模型。我们可以考虑增加使用DeZero的实现实例。用DeZero实现GAN(参考文献[41])、VAE(参考文献[42])和Style Transfer(参考文献[43])等著名的研究成果是展示如何使用DeZero的一个好办法。通过这样的工作，我们还可以发现DeZero缺失的功能。另外，在dezero/examples中有一些使用DeZero的实示例(预计会继续增加)，感兴趣的读者可以参考。

附录A

in-place 运算

(步骤14的补充内容)

本附录内容是对步骤14的补充，这里笔者会对步骤14中所说的“在导数加法计算时不使用 $+=$ ”的原因进行说明。