26.4 代码验证

现在试着将步骤24中实现的Goldstein-Price函数可视化。代码如下所示。

steps/step26.py

import numpy as np   
fromdezero import Variable   
fromdezero.utils import plotidot_graph   
def goldstein(x,y):  $z = (1 + (x + y + 1)**2*(19 - 14*x + 3*x**2 - 14*y + 6*x*y + 3*y**2))*\backslash$ $(30 + (2*x - 3*y)**2*(18 - 32*x + 12*x**2 + 48*y - 36*x*y + 27*y**2))$  return z   
 $x =$  Variable(np.array(1.0))   
 $y =$  Variable(np.array(1.0))   
 $z =$  goldstein(x,y)   
z.backup()   
 $x.name = 'x'$ $y.name = 'y'$ $z.name = 'z'$    
plotidot_graph(z,verbose=False,to_file='goldstein.png')

运行上面的代码会得到文件goldstein.png。结果如图26-3所示，这是一个各种变量和函数交织在一起的计算图。仔细观察会发现该计算图以输入变量x和y为始，以输出变量z为终。这里多说两句，在使用DeZero实现Goldstein-Price函数时，我们几乎将式子直接照搬在代码中，但其实DeZero在幕后创建了图26-3这种错综复杂的计算图。

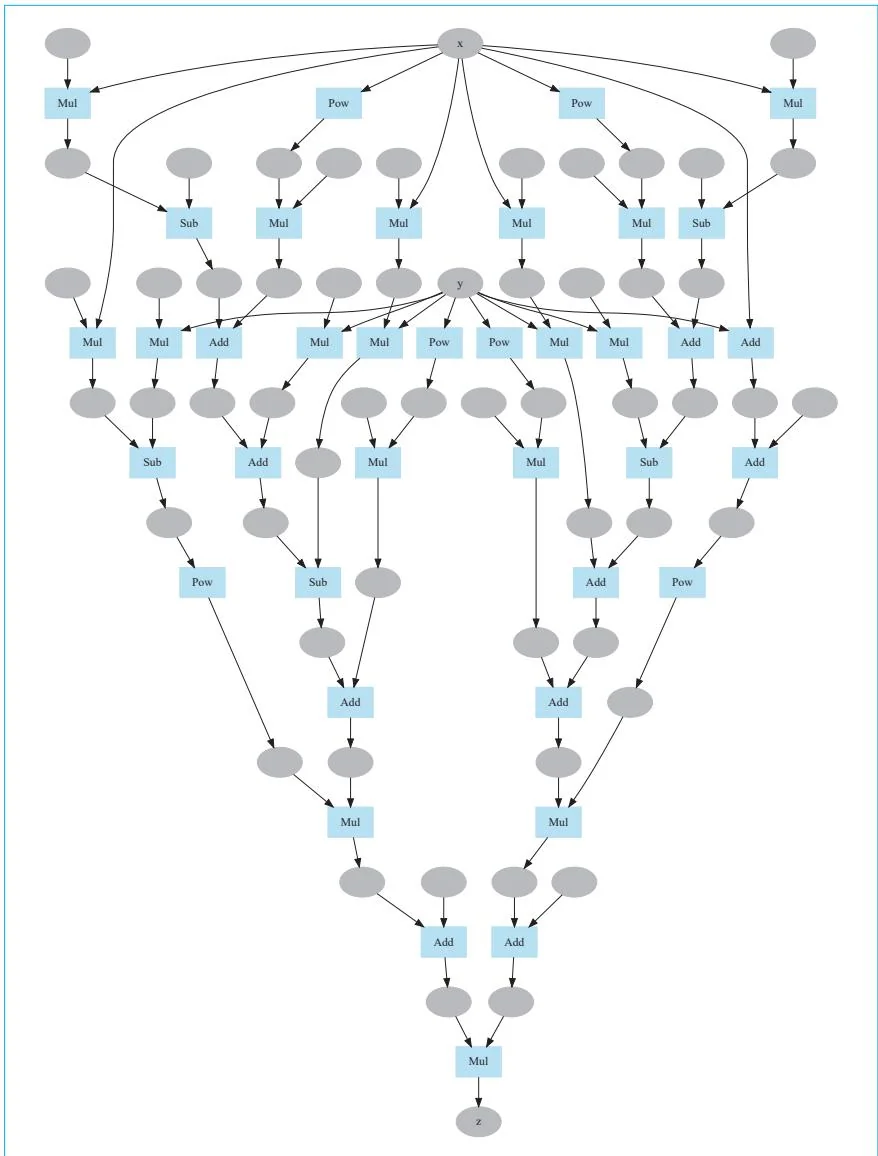
图26-3 Goldstein-Price函数的计算图

到这里就完成了计算图的可视化。将来我们会根据需要使用这里实现的函数。

步骤27

泰勒展开的导数

下面使用DeZero解决一些具体问题。我们先来思考一下sin函数的导数。它的导数当然可以通过解析方式求出。这里我们采用“正面进攻”的做法，也就是使用DeZero直接实现sin函数，然后尝试使用泰勒展开式求出sin函数的导数。