16.4 代码验证

现在我们可以按照 generation 的值从大到小的顺序取出函数了。这样一来，无论计算图多么复杂，反向传播应该都能以正确的顺序进行。下面试着求出图 16-4 这个计算的导数。计算图和代码如下所示。

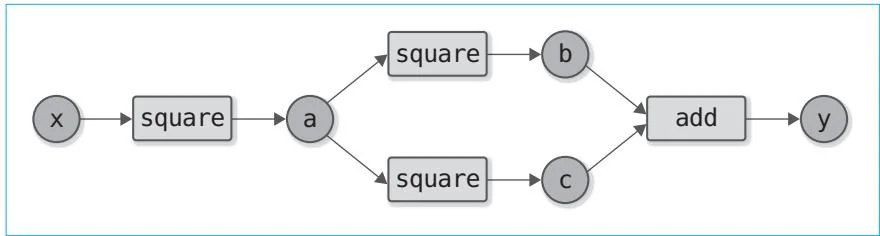
图16-4 此前无法正确处理的计算图的例子

steps/step16.py   
 $\begin{array}{rl} & {\mathrm{x} = \mathrm{Variable}(\mathrm{np.array}(2.0))}\\ & {\mathrm{a} = \mathrm{square}(\mathrm{x})}\\ & {\mathrm{y} = \mathrm{add}(\mathrm{square}(\mathrm{a}),\mathrm{square}(\mathrm{a}))}\\ & {\mathrm{y}.}\end{array}$  backward()   
print(y.data)   
print(x.grad)

运行结果 32.0 64.0

从运行结果来看，求出的 $x$ 的导数是 64.0。我们使用式子来确认一下，也就是求 $y = (x^2)^2 + (x^2)^2$ ，即 $y = 2x^4$ 的导数。由于 $y' = 8x^3$ ，所以 $x = 2.0$ 时的导数为 64.0，与上面的运行结果一致。

我们终于可以处理复杂的计算图了。图16-4所示的计算图比较简单，但其实DeZero已经可以对连接方式比较复杂的计算图求导了，比如图16-5这样的计算图。

图16-5 连接方式更加复杂的计算图的例子（步骤35中实际创建的y = tanh(x)的四阶导数的计算图）

本步骤到此结束。这个步骤是整本书中比较难的一个部分。理解了这个步骤的内容，大家就能很快感受到DeZero的威力了。在下一个步骤，我们来看看DeZero的性能，特别是它的内存使用情况。

步骤17

内存管理和循环引用

DeZero 是一个重视教学的通俗易懂的框架，所以牺牲了一些性能。我们此前确实也没有关注速度和内存的使用情况。在本步骤和下一个步骤，我们会向 DeZero 引入一些可以提高性能的技术。首先来学习一下 Python 的内存管理。

Python是一门编程语言，它其实也是一个执行Python代码的程序。这个程序通常称为Python解释器。默认的Python解释器是CPython，它是用C语言实现的。本步骤按照CPython的做法对Python内存管理进行说明。