13.1 支持可变长参数的Add类的反向传播

在实现反向传播之前，我们先来看看图13-1中加法运算的计算图。

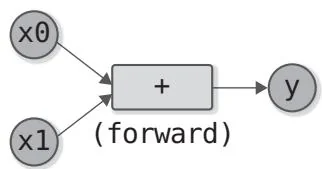
图13-1 加法运算计算图的正向传播和反向传播（求 $y = x0 + x1$ 的导数的函数用 $+'$ 表示）。

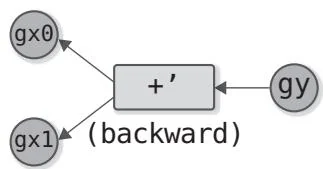
如图13-1所示，加法运算的正向传播有两个输入和一个输出。反向传播的情况正好相反，有一个输入和两个输出。从表达式来看，当 $y = x_0 + x_1$ 时，由导数公式可得 $\frac{\partial y}{\partial x_0} = 1$ ， $\frac{\partial y}{\partial x_1} = 1$ 。

式子（函数） $y = x_{0} + x_{1}$ 有两个输入变量。这种有多个输入变量的函数称为多元函数。在多元函数中，只对一个输入变量求导（将其他变量视为常数），得到的是偏导数。偏导数的导数符号是 $\partial$ 。拿例子中的 $\frac{\partial y}{\partial x_0}$ 来说，它表示我们只关注 $x_{0}$ 并对其求导， $x_{0}$ 以外的变量一律视为常数。本书在后面提到偏导数时，也会将其简称为导数。此外，即使是仅有一个变量的情况，在式子中我们也会使用符号 $\partial$ 。

在加法运算的反向传播中，从输出端传播的导数乘以1后的值就是输入变量 $(x_0, x_1)$ 的导数。换言之，加法运算的反向传播就是把上游的导数原封不动地“传走”。考虑到这些内容，我们按如下方式实现Add类。

steps/step13.py

class Add(Function): def forward(self, x0, x1): y = x0 + x1 return y def backward(self, gy): return gy, gy

在上面的代码中，backward方法有一个输入和两个输出。当然，为了支持这种有多个返回值的情况，我们必须修改反向传播的实现。在DeZero中，这是通过Variable类的backward方法实现的。