31.1 在反向传播时进行的计算

与正向传播一样，反向传播也会进行具体的计算。以上一个步骤的Sin类为例，实现backward方法的代码如下所示。

class Sin(Function): def backward(self, gy): x = self.inputs[0].data gx = gy * np.cos(x) return gx

上面的代码进行了 $\mathrm{gx = gy*np.cos(x)}$ 这个具体的计算。但是，当前的DeZero不会为该计算创建计算图，因为该计算针对的是ndarray实例。如果能对反向传播所进行的计算创建连接，会发生什么呢？答案是高阶导数会被自动计算出来。在解释这个原理之前，我们先来看看图31-1中的计算图。

图31-1 $y = \sin(x)$ 的计算图

图31-1是 $y = \sin(x)$ 的计算图。调用y.backup()即可求出y对x的导数。这是我们已经见过的例子。现在来看一下图31-2的计算图。

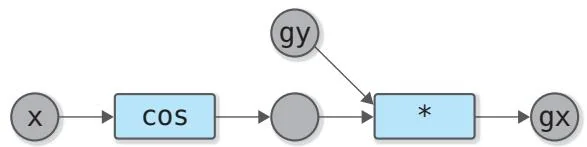
图31-2 用于求 $y = \sin (x)$ 的导数的计算图（gx是y对x的导数）

图31-2中的计算图用于求sin函数的导数。该图以计算图的形式展示了前面Sin类的反向传播的代码 $(gx = gy * np.cos(x))$ 。对于图31-2这样的计算图，我们可以通过调用gx.backup()求出gx对x的导数。由于gx本来就是 $y = \sin (x)$ 的导数，所以调用gx.backup()可以对x再次求导，也就是求x的二阶导数。

如果理解不了上面的内容，你也可以把图31-2中的x当作时间，把gx当作速度来进行思考。这样来看，图31-2就表示一个输入某时间后输出在该时间的速度的计算图。此时通过反向传播求出的是速度对时间的导数，结果对应的是加速度。

接下来我们要做的是将图31-2这种求导计算作为计算图创建出来。求导计算换句话说就是通过反向传播进行计算。因此，如果能为反向传播进行的计算建立连接，就可以解决这个问题。下面我们来思考一下具体的实现方法。