10.4 测试小结

在创建DeZero方面，关于测试，了解以上知识就足够了。读者可以根据前面的步骤编写DeZero的测试代码。不过，本书之后的内容省略了测试相关的说明。如果读者觉得需要添加测试代码，请自行编写。

通常，我们会在一个地方汇总管理所有测试代码文件。本书的测试代码也统一放在 tests 目录下（该目录下还包含了另行实现的用于测试的工具函数的代码）。有兴趣的读者可以看看这些测试代码，其中很多代码与我们在本步骤编写的代码类似。可以使用以下命令一起运行所有测试文件。

$ python -m unittest discover tests

像这样使用 discover 子命令后，discover 会在其后指定的目录下搜索测试文件，然后将所有找到的文件一起运行。在默认情况下，指定目录下符合 test*.py 模式的文件会被识别为测试文件（模式可以修改）。这样就能一次性运行 tests 目录下的所有测试文件了。

DeZero的tests目录下也有以Chainer的结果为正确答案的测试。例如在测试sigmoid函数时，测试代码使用DeZero和Chainer分别对相同的输入进行计算，然后比较这两个输出是否大体相同。

DeZero 的 GitHub 仓库还集成了 Travis CI（参考文献 [9]）。Travis CI 是一个持续集成服务。在对 DeZero 的 GitHub 仓库①的代码进行 push 和 Pull Request 操作时，测试会自动运行。如果结果有问题，Travis CI 会通过电子邮件通知。另外，DeZero 的 GitHub 仓库首页会显示图 10-1 这样的界面。

图10-1 DeZero的GitHub仓库的首页界面

pypi v0.0.11

license MIT

build p

ssing

如图10-1所示，界面上会显示“build: passing”徽章。这个徽章意味着测试通过（如果测试失败，界面上会显示“build: failed”徽章）。通过与CI工具的协作，源代码能够不断得到测试。这样可以确保代码的可靠性。

DeZero现在还是一个小软件，我们会把它发展成更大的软件。引入本步骤介绍的测试机制后，我们有望持续保持代码的可靠性。以上就是第1阶段的内容。

★★★★★★★

在第1阶段，我们一步一个脚印地创建了DeZero。最初的DeZero只有一个“小箱子”(变量)，现在它已经发展到能够运行反向传播这种复杂算法的规模了。但是，现在实现的反向传播只能应用于简单的计算。从下一个阶段开始，我们将进一步扩展DeZero，使其可以应用于更复杂的计算。

专栏：自动微分

深度学习框架的核心技术是反向传播。有些资料将反向传播称为“自动微分”。需要注意的是，“自动微分”指代的是范围更加具体的一种技术，在学术领域尤其如此。下面是对自动微分的补充说明。

自动微分指的是自动求出导数的做法（技术）。“自动求出导数”是指由计算机（而非人）求出导数。具体来说，它是指在对某个计算（函数）编码后，计算机会自动求出该计算的导数的系统。

计算机程序求导的方法主要有3种。

第1种方法是数值微分。如同步骤4中实现的那样，首先给变量以微小的差异并执行普通计算（正向传播），重复两次该操作，然后基于输出的差值计算得到近似的导数。数值微分虽然容易实现，但也存在一些问题，比如输出中包含误差、在处理多变量的函数时计算成本高等。

第2种方法是符号微分（symbolic differentiation）。这是使用导数公式求导的方法。输入是式子，输出也是式子(式子可以用树状结构的数据形式表示)。这种方法被用在Mathematica和MATLAB等软件中。

符号微分的输出是求导后的表达式，即导函数，这时还没有进行任何数值计算。在得到导函数之后，我们就可以求出某个特定值（如 $x = 3.0$ ）上的导数了。

符号微分的问题是式子很容易变得臃肿。特别是在不考虑优化的实现中，式子很快就会变“大”（可以说是式子“大爆炸”）。但深度学习中处理的计算需要高效地对大量变量求出导数“值”（而不是表达式），这就需要使用更合适的方法了。

第3种方法是自动微分。这是一种采用链式法则求导的方法。我们对某个函数编码后，可以通过自动微分高效地求出高精度的导数。反向传播也是自动微分

的一种。更准确地说，自动微分可以大体分为两种：前向模式的自动微分和反向模式的自动微分。反向传播相当于反向模式的自动微分。

反向传播（反向模式的自动微分）将导数从输出到输入的方向传播。前向模式的自动微分则与之相反，导数的传播方向是从输入到输出。这两种方法都利用链式法则来求导，但路径并不相同。如果输出只有一个，要计算的是这个输出变量的导数，那使用反向模式的自动微分再合适不过了。许多机器学习问题的输出是一个变量，所以使用反向模式的自动微分。本书不对前向模式的自动微分做过多说明，对前向模式的自动微分感兴趣的读者可以阅读参考文献[6]和参考文献[7]。

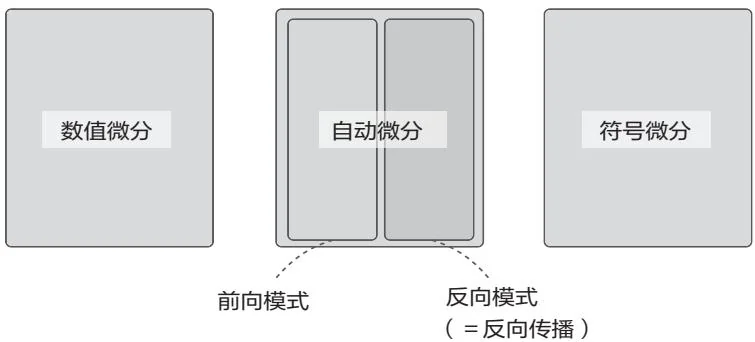
图A-1 汇总了前面介绍的计算机程序求导的方法

如图A-1所示，自动微分是用计算机求导的一种方法。深度学习框架中实现的是反向模式的自动微分。不过有些资料不区分前向模式和反向模式，笼统地将反向传播称为“自动微分”。

在学术领域，自动微分的研究有很长的历史，积累了许多重要的研究成果。遗憾的是，此前自动微分与机器学习领域没有什么交集。近来，随着深度学习的蓬勃发展，自动微分领域受到越来越多的关注，机器学习和编程语言等领域与自动微分领域开始了新的交流。

第2阶段

用自然的代码表达

我们已经完成了构建DeZero的第1阶段的工作，现在它可以自动求出特定计算的导数。假设计算图由平方或指数函数等函数类组成(笔直的计算图)，它的导数就可以通过调用backward方法自动求得。

下面进入第2阶段。这个阶段的主要目标是扩展当前的DeZero，使它能够执行更复杂的计算。具体来说，我们将修改DeZero的基础代码，使它能够处理接收多个输入的函数和返回多个输出的函数。我们还将扩展DeZero，使它可以用自然的代码来表达，例如能够使用 $^+$ 和 $\ast$ 等运算符。

第2阶段结束时，DeZero会被打包为一个Python包。这样，第三方也能使用DeZero了。下面进入第2阶段吧！

步骤11

可变长参数（正向传播篇）

之前涉及的函数，其输入输出都只有一个变量，如 $y = \text{square}(x)$ 和 $y = \exp(x)$ 等，但有些函数需要多个变量作为输入，例如图11-1所示的加法运算和乘法运算的情况。

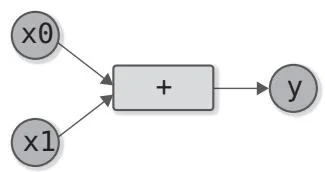
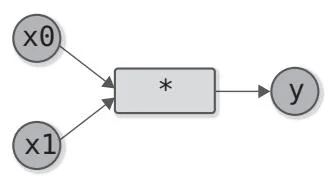
图11-1 加法运算的计算图和乘法运算的计算图（乘法运算用*表示）

另外，有些函数可能有多个输出，例如图11-2所示的函数。

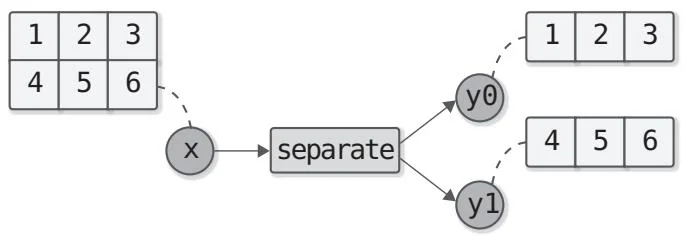
图11-2 有多个输出的计算图示例（分割多维数组的函数）

考虑到这些情况，我们来扩展DeZero，使其可以处理可变长的输入和输出。可变长意味着参数(或返回值)的数量可以发生变化，数量可以是不小于1的任意整数值。下面修改Function类以支持可变长的参数和返回值。