42.4 DeZero的mean_squared_error函数(补充内容)

前面我们实现了求均方误差的函数。代码摘录如下。

steps/step42.py

def mean_squared_error(x0, x1):
    diff = x0 - x1
    y = F.sum(diff ** 2) / len(diff)
    return y

这个函数正确地进行了计算。此处是用DeZero函数进行计算的，所以也能求导。不过，当前实现还有一些地方需要改进。为了方便说明，我们先看一下图42-6的计算图。

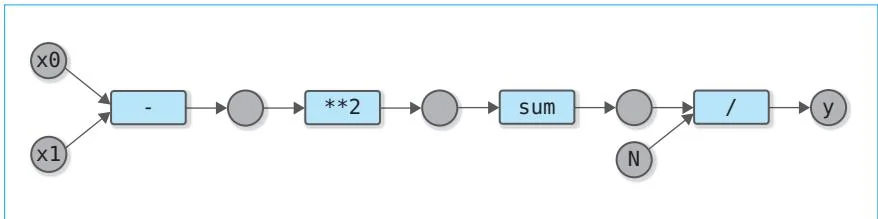
图42-6 mean_squared_error函数的计算图

图42-6是由上面的mean_squared_error函数产生的计算图。我们需要关注的是中间的变量。这里有3个匿名变量。由于这些变量记录在计算图里，所以只要计算图存在，它们就会一直保存在内存中。这些变量的数据（ndarray实例）也将一直存在。

DeZero在求导时首先进行正向传播，然后进行反向传播。图42-6中的变量(以及它们引用的数据)在正向传播和反向传播期间都保存在内存中。

如果内存的使用量不存在问题，那么上面的实现方法也没有问题。不过这种会被第三方使用的函数有更好的实现方法，即继承Function类进行实现，也就是实现一个名为MeanSquaredError的DeZero函数类。实际的代码如下所示。

dezero/functions.py

class MeanSquaredError(Function): def forward(self, x0, x1): diff = x0 - x1 y = (diff ** 2).sum() / len(diff) return y def backward(self, gy): x0, x1 = self.inputs diff = x0 - x1 gx0 = gy * diff * (2. / len(diff)) gx1 = -gx0 return gx0, gx1   
def mean_squared_error(x0, x1): return MeanSquaredError((x0, x1)

首先在正向传播中以ndarray实例为对象。这段代码与之前DeZero版本的函数中实现的代码几乎相同。然后将反向传播的代码汇总到一起实现backward方法。反向传播的实现具体来说就是通过式子求导后将其编写成代码。此处不再赘述。

用新方法实现的mean_squared_error函数能得到与之前的版本相同的结果。但从内存效率上来说，新的实现方法更好。这是为什么呢？我们看一下新的mean_squared_error函数的计算图(图42-7)。

图42-7 新的mean_squared_error函数的计算图

将图42-7与旧的计算图(图42-6)比较可知，新的计算图中没有中间变量。中间的数据只用在MeanSquaredError类的forward方法中。准确来说，它们作为ndarray实例使用，一旦离开forward方法的作用范围，就马上从内存中被清除。

出于以上原因，我们使用新的方式实现了dezero/functions.py中的mean_squared_error函数。为了便于参考，旧的实现方式被命名为mean_squared_error.simple(在原名后附上了simple)，添加到dezero/functions.py中。以上就是对DeZero的mean_squared_error函数的补充说明。