4.1 什么是导数

什么是导数？简单地说，导数是变化率的一种表示方式。比如某个物体的位置相对于时间的变化率就是位置的导数，即速度。速度相对于时间的变化率就是速度的导数，即加速度。像这样，导数表示的是变化率，它被定义为在极短时间内的变化量。函数 $f(x)$ 在 $x$ 处的导数可用下面的式子表示。

式子4.1中的 $\lim_{h\to 0}$ 表示极限，意思是 $h$ 应尽可能地接近0。式子4.1中的

$\frac{f(x + h) - f(x)}{h}$ 为图4-1中通过两点的直线的斜率。

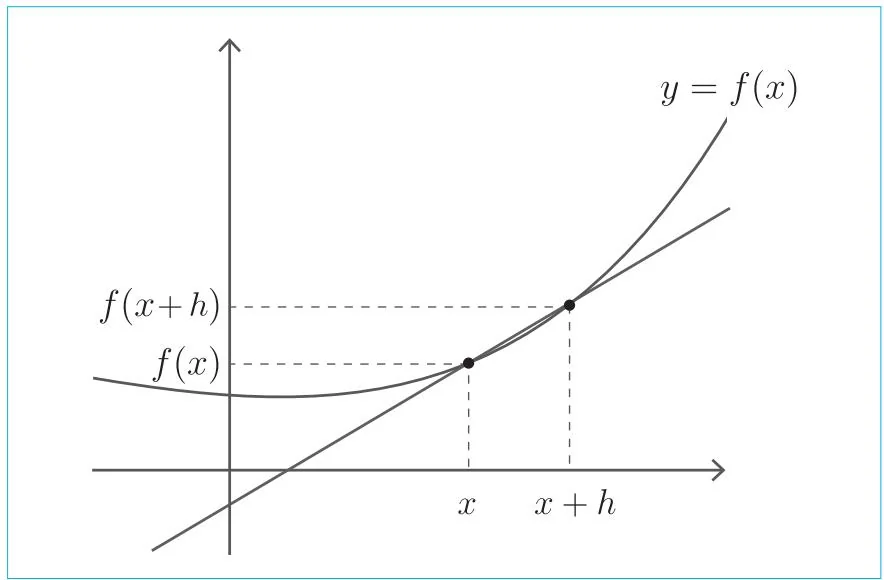
图4-1 曲线 $y = f(x)$ 和通过其两点的直线

如图4-1所示，函数 $f(x)$ 在 $x$ 和 $x + h$ 两点之间的变化率为 $\frac{f(x + h) - f(x)}{h}$ 。让 $h$ 的值尽可能地接近0，就可以求出 $x$ 处的变化率。这就是 $y = f(x)$ 的导数。另外，在 $y = f(x)$ 的可导区间内，对于该区间内的任何 $x$ ，式子4.1都成立。因此，式子4.1中的 $f'(x)$ 也是一个函数，我们称之为 $f(x)$ 的导函数。