34.3 sin函数的高阶导数

下面试着求sin函数的高阶导数。这次不仅要尝试求二阶导数，还要求三阶导数和四阶导数。代码如下所示。

import numpy as np   
fromdezero import Variable   
importdezero-functionsasF   
 $\texttt{x} =$  Variable(np.array(1.0))   
y  $=$  F.sin(x)   
y.backupcreate_graph  $\equiv$  True)   
fori in range(3): gx=x.grad x.cleargrad() gx.backupcreate_graph  $\equiv$  True) print(x.grad）#n阶导数

运行结果

variable(-0.8414709848078965)  
variable(-0.5403023058681398)  
variable(0.8414709848078965)

上面的代码使用for语句来重复进行反向传播。这样就能求出二阶导数、三阶导数等 $n$ 阶导数了。for语句中的代码与之前的相同。具体来说，就是使用 $\mathtt{gx} = \mathtt{x}$ .grad取出导数，然后从gx进行反向传播。在进行反向传播之前，调用x.cleargrad()来重置导数。重复这个过程，就可以得到 $n$ 阶导数。

上面的代码中用来执行导入操作的代码是 importdezero-functions as F。由此我们就可以使用F.sin()和F.cos()这样的写法了。今后我们还会在dezero/functions.py中增加各种函数，到时F.xxx()这种写法会非常方便。

接下来在前面代码的基础上编写绘制图像的代码。修改后的代码如下所示。

steps/step34.py

import numpy as np   
import matplotlib.pyplot as plt   
fromdezero import Variable   
importdezero-functions as F   
 $\texttt{x} =$  Variable(np.linspace(-7,7,200))   
y  $=$  F.sin(x)   
y.backupcreate_graph  $\equiv$  True)   
logs  $=$  [y.data]   
for i in range(3): logs.append(x.grad.data) gx  $=$  x.grad   
x.cleargrad() gx.backupcreate_graph  $\equiv$  True)

绘制图像

labels = ["y=sin(x)", "y","y''","y''"]  
for i, v in enumerate(logs):  
    plt.plot(x.data, logs[i], label=labels[i])  
plt.legend(loc='lower right')  
plt.show()

这段代码与前面代码的主要区别是输入的变量变成了 $x = \text{Variable}(\text{np.linspace}(-7, 7, 200))$ 。这里的 np.linspace(-7, 7, 200) 会创建一个数组，该

数组包含200个-7到7均匀间隔的数。具体来说，这是一个一维数组，值为[-7., -6.92964824, -6.85929648, ..., 7.]。上面的代码将这个一维数组封装在了Variable中。

除输入变量变为一维数组外，求高阶导数的代码与之前的完全相同。当输入多维数组时，此前实现的DeZero函数会对每个元素分别执行计算。因此，200个元素可以一次(正向传播)完成计算。

输入多维数组时，很多NumPy的函数会分别计算每个元素。在正向传播时，DeZero的函数使用NumPy的函数来计算ndarray实例。因此，如果向DeZero函数输入多维数组，DeZero函数将逐元素进行计算。

执行上面的代码，结果如图34-1所示。

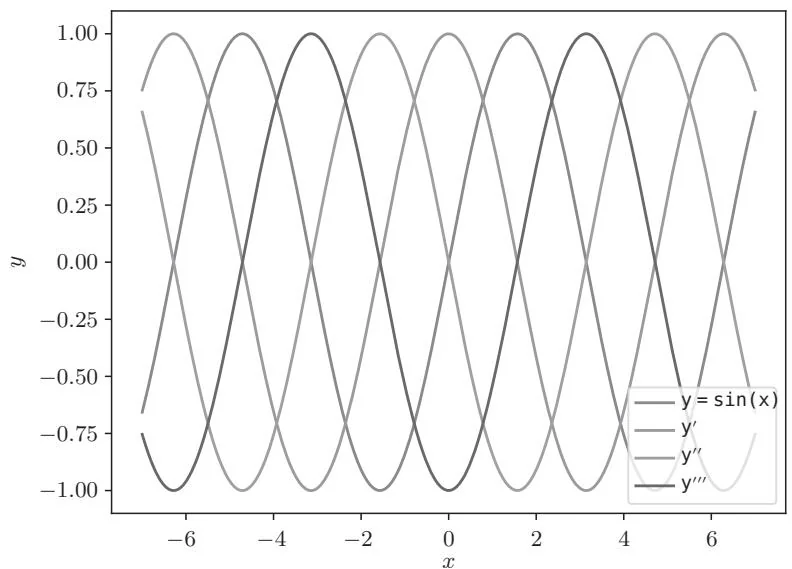
图34-1 y=sin(x)及其高阶导数的图像(标签y'对应一阶导数，y''对应二阶导数，y''对应三阶导数。参见彩图)

图34-1是 $y = \sin(x)$ 和它的高阶导数的图像，其展示了波的相位发生了偏移的函数。之所以这么说，是因为按照一阶导数、二阶导数、三阶导数这种方式不断求导，函数也会不断发生变化，即 $y = \sin(x) \rightarrow y = \cos(x) \rightarrow y = -\sin(x) \rightarrow y = -\cos(x)$ 。

本步骤到此结束。本步骤重新实现了DeZero的sin函数和cos函数。在下一个步骤，我们将继续增加新的DeZero函数。

步骤35

高阶导数的计算图

紧接着上一个步骤的内容，本步骤将继续增加DeZero的函数。这里要增加的是tanh函数，tanh表示双曲正切，tanh函数可用式子35.1表示，其图像如图35-1所示。

图35-1 tanh函数的图像

如图35-1所示，tanh函数将输入转化为-1和1之间的值。首先求式子35.1的导数 $\frac{\partial y}{\partial x}$