41.1 向量的内积和矩阵的乘积

下面介绍向量的内积和矩阵的乘积。首先是向量的内积。假设有向量 $\mathbf{a} = (a_{1},\dots ,a_{n})$ 和向量 $\pmb {b} = (b_{1},\dots ,b_{n})$ 。向量的内积可以定义为式子41.1。

如式子41.1所示，把两个向量间相应元素的乘积相加，得到的就是向量的内积。

这里对式子中符号的使用做一些规定。我们使用 $a$ 、 $b$ 这样的符号表示标量，使用 $\mathbf{a}$ 、 $\mathbf{b}$ 这样的粗体符号表示向量和矩阵。

接下来是矩阵的乘积。矩阵乘积的计算方法如图41-1所示。

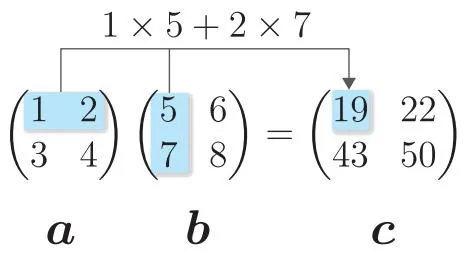
图41-1 矩阵乘积的计算方法

如图41-1所示，矩阵乘积的计算方法是先分别求出左侧矩阵水平方向的向量和右侧矩阵垂直方向的向量的内积，然后将结果存储在新矩阵的相应元素中。例如， $\pmb{a}$ 的第1行和 $\pmb{b}$ 的第1列的结果是新矩阵第1行第1列的元素， $\pmb{a}$ 的第2行和 $\pmb{b}$ 的第1列的结果是新矩阵第2行第1列的元素，以此类推。

下面使用NumPy来实现向量的内积和矩阵的乘积。为此，我们需要使用np.dot函数。

import numpy as np

向量的内积

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.dot(a, b)
print(c)

矩阵的乘积

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
c = np.dot(a, b)
print(c)

运行结果

32  
[[19, 22], [43, 50]]

如代码所示，在计算向量的内积和矩阵的乘积时都可以使用np.dot函数。如果np.dot(x，y)的两个参数都是一维数组，函数计算的就是向量的内积；如果两个参数都是二维数组，函数计算的就是矩阵的乘积。