0x23 剪枝

剪枝，就是减小搜索树规模、尽早排除搜索树中不必要的分支的一种手段。形象地看，就好像剪掉了搜索树的枝条，故称之为“剪枝”。在深度优先搜索中，有以下几类常见的剪枝方法：

1.优化搜索顺序

在一些搜索问题中，搜索树的各个层次、各个分支之间的顺序不是固定的。不同的

搜索顺序会产生不同的搜索树形态，其规模大小也相差甚远。例如：

(1)在上一节的“小猫爬山”问题中，把小猫按照重量递减的顺序进行搜索。
(2) 在上一节的“Sudoku”问题中，优先搜索“能填的合法数字”最少的位置。

2. 排除等效冗余

在搜索过程中，如果我们能够判定从搜索树的当前节点上沿着某几条不同分支到达的子树是等效的，那么只需要对其中的一条分支执行搜索。我们会在本节的“Sticks”问题中看到该剪枝的应用。

另外，就如我们在上一节的“Sudu”问题中提出的，初学者一定要避免重叠、混淆“层次”与“分支”，避免遍历若干棵覆盖同一状态空间的等效搜索树。

3. 可行性剪枝

在搜索过程中，及时对当前状态进行检查，如果发现分支已经无法到达递归边界，就执行回溯。这就好比我们在道路上行走时，远远看到前方是一个死胡同，就应该立即折返绕路，而不是走到路的尽头再返回。

某些题目条件的范围限制是一个区间，此时可行性剪枝也被称为“上下界剪枝”。

4. 最优性剪枝

在最优化问题的搜索过程中，如果当前花费的代价已经超过了当前搜到的最优解，那么无论采取多么优秀的策略到达递归边界，都不可能更新答案。此时可以停止对当前分支的搜索，执行回溯。

5. 记忆化

可以记录每个状态的搜索结果，在重复遍历一个状态时直接检索并返回。这就好比我们对图进行深度优先遍历时，标记一个节点是否已经被访问过。

不过，读者可能已经发现，在“小猫爬山”与“Sudoku”问题中，我们的搜索算法遍历的状态空间其实是“树”形，不会重复访问，所以不需要进行记录。

在本节中，我们通过几道例题来了解这些剪枝方法的具体应用。

【例题】Sticks FOJ1011

乔治拿来一组等长的木棒，将它们随机地砍断，得到若干根小木棍，并使每一节木棍的长度都不超过50个长度单位。然后他又想把这些木棍拼接起来，恢复到裁剪前的状态，但他忘记了初始时有多少木棒以及木棒的初始长度。请你设计一个程序，帮助乔治计算木棒的可能最小长度。每一节木棍的长度都用大于零的整数表示。

输入包含多组数据，每组数据包括两行。第一行是一个不超过64的整数，表示砍断之后共有多少节木棍。第二行是截断以后，所得到的各节木棍的长度。在最后一组数据之后，是一个零。

对于每组数据，分别输出原始木棒的可能最小长度。

我们可以从小到大枚举原始木棒的长度len（也就是枚举答案）。当然，len应该是所有木棍长度总和sum的约数，并且原始木棒的根数cnt就等于sum/len。

对于枚举的每个len，我们可以依次搜索每根原始木棒由哪些木棍拼成。具体地讲，搜索所面对的状态包括：已经拼好的原始木棒根数，正在拼的原始木棒的当前长度，每个木棍的使用情况。在每个状态下，我们从尚未使用的木棍中选择一个，尝试拼到当前的原始木棒里，然后递归到新的状态。递归边界就是成功拼好cnt根原始木棒，或者因无法继续拼接而宣告失败。

这个算法的效率比较低，我们来依次考虑几类剪枝：

1.优化搜索顺序

把木棍长度从大到小排序，优先尝试较长的木棍。

1. 排除等效冗余

(1) 可以限制先后加入一根原始木棒的木棍长度是递减 $(\geq)$ 的。这是因为先拼上一根长度为 $x$ 的木棍，再拼上一根长为 $y$ 的木棍 $(x < y)$ ，与先拼上 $y$ 再拼上 $x$ 显然是等效的，只需要搜索其中一种。
(2) 对于每根原始木棒，记录最近一次尝试拼接的木棍长度。如果分支搜索失败回溯，不再尝试向该木棒中拼接其他相同长度的木棍（必定也会失败）。
(3) 如果在一根原始木棒中尝试拼接的第一根木棍的递归分支就以失败返回，直接判定当前分支无解。这是因为目前剩余的原始木棒都是“空”的（还没有进行拼接），这些木棒是等效的。木棍拼在当前的木棒中失败，拼在其他木棒中一样会失败。

上述(1)至(3)三点分别利用了“同一根木棒上木棍顺序的等效性”“等长木棍的等效性”“空木棒的等效性”，剪掉了搜索树上诸多分支，使得搜索效率大大提升。

int a[100], v[100], n, len, cnt;  
// 正在拼第 stick 根原始木棒（已经拼好了 stick-1 根）  
// 第 stick 根木棒的当前长度为 cab  
// 拼接到第 stick 根木棒中的上一根小木棍为 last  
bool dfs(int stick, int cab, int last) {  
// 所有原始木棒已经全部拼好，搜索成功  
if (stick > cnt) return true;  
// 第 stick 根木棒已经拼好，去拼下一根  
if (cab == len) return dfs(stick + 1, 0, 1);  
int fail = 0; // 剪枝(b)  
// 剪枝(a): 小木棍长度递减（从 last 开始枚举）  
for (int i = last; i <= n; i++)  
if (!v[i] && cab + a[i] <= len && fail != a[i]) {

$\begin{array}{l}\mathrm{v[i] = 1;}\\ \mathrm{if~(dfs(stick,cab + a[i],i + 1))~return~true;}\\ \mathrm{fail = a[i];}\\ \mathrm{v[i] = 0; //~还原现场}\\ \mathrm{if~(cab == 0)~return~false; //~剪枝(c)}\\ \} \\ \mathrm{return~false; //~所有分支均尝试过，搜索失败} \end{array}$    
int main() {while (cin >> n && n){int sum  $= 0$  ,val  $= 0$  for(int i  $= 1$  ;i  $<   =$  n;i++) {scanf("%d",&a[i]);sum  $+ =$  a[i];val  $=$  max(val,a[i]);1sort(a  $+1$  ，a+n+1);reverse(a+1,a+n+1);for(len  $=$  val;len  $<   =$  sum;len++) {if (sum % len) continue;cnt  $=$  sum / len; //原始木棒长度为len，共cnt根memset(v,0,sizeof(v));if (dfs(1,0,1)) break;1cout<<len<<endl;

【例题】生日蛋糕 POJJ1190

Mr. W 要制作一个体积为 $N\pi$ 的 $M$ 层生日蛋糕，每层都是一个圆柱体。

设从下往上数第 $i(1 \leq i \leq M)$ 层蛋糕是半径为 $R_{i}$ , 高度为 $H_{i}$ 的圆柱。当 $i < M$ 时, 要求 $R_{i} > R_{i} + 1$ 且 $H_{i} > H_{i} + 1$ 。

因为要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积 $Q$ 最小。

记 $Q = S\pi$ ，请编程对给出的 $N$ 和 $M$ ，找出一种蛋糕的制作方案（适当的 $R_{i}$ 和 $H_{i}$ 的值），使 $S$ 最小。

除 $Q$ 外，以上所有符号皆表示正整数， $N \leq 10000, M \leq 20$ ，圆柱体积 $V = \pi R^2 H$

侧面积 $A^{\prime} = 2\pi RH$ ，底面积 $A = \pi R^2$ 。

搜索框架：从下往上搜索，枚举每层的半径和高度作为分支。

搜索面对的状态有：正在搜索蛋糕第 dep 层，当前外表面面积 $s$ ，当前体积 $v$ ，第 dep + 1 层的高度和半径。不妨用数组 $h$ 和 $r$ 分别记录每层的高度和半径。

整个蛋糕的“上表面”面积之和等于最底层的圆面积，可以在第 $M$ 层直接累加到 $s$ 中。这样在第 $M - 1$ 层往上的搜索中，只需要计算侧面积。

剪枝：

1.上下界剪枝

在第 dep 层时，只在下面的范围内枚举半径和高度即可。

首先，枚举 $R \in [dep, \min(\lfloor \sqrt{N - v} \rfloor, r[dep + 1] - 1)]$ 。

其次，枚举 $H \in [dep, \min(\lfloor (N - v) / R^2 \rfloor, h[dep + 1] - 1)]$ 。

上面两个区间右边界中的式子可以通过圆柱体积公式 $\pi R^2 H = \pi (N - v)$ 得到。

2.优化搜索顺序

在上面确定的范围中，使用倒序枚举。

3.可行性剪枝

可以预处理出从上往下前 $i(1 \leq i \leq M)$ 层的最小体积和侧面积。显然，当第 $1 \sim i$ 层的半径分别取 $1, 2, 3, \dots, i$ ，高度也分别取 $1, 2, 3, \dots, i$ 时，有最小体积与侧面积。

如果当前体积 $v$ 加上 $1 \sim dep - 1$ 层的最小体积大于 $N$ ，可以剪枝。

4. 最优性剪枝一

如果当前表面积 $s$ 加上 $1 \sim dep - 1$ 层的最小侧面积大于已经搜到的答案，剪枝。

5. 最优性剪枝二

利用 $h$ 与 $r$ 数组， $1 \sim dep - 1$ 层的体积可表示为 $n - v = \sum_{k=1}^{dep-1} h[k] * r[k]^2$ , $1 \sim dep - 1$ 层的表面积可表示为 $2 \sum_{k=1}^{dep-1} h[k] * r[k]$ 。

因为 $2\sum_{k = 1}^{dep - 1}h[k]*r[k] = \frac{2}{r[dep]}\ast \sum_{k = 1}^{dep - 1}h[k]*r[k]*r[dep]\geq \frac{2}{r[dep]}\ast \sum_{k = 1}^{dep - 1}h[k]*$ $r[k]^2\geq \frac{2(n - v)}{r[dep]},$ 所以当 $\frac{2(n - v)}{r[dep]} +s$ 大于已经搜到的答案时，可以剪枝。

加入以上五个剪枝后，搜索算法就可以快速求出该问题的最优解了。

实际上，搜索算法面对的状态可以看作一个多元组，其中每一元都是问题状态空间中的一个“维度”。例如本题中，层数 $dep$ 、表面积 $s$ 、体积 $v$ 、第 $dep + 1$ 层的高度和半径就构成状态空间中的五个维度，其中每一项发生变化，都会移动到状态空间中的另一个“点”。这些维度通常在题目描述中也有所体现，它们一般在输入变量、限制条件、待求解变量等非常关键的位置出现。读者一定要注意提取这些“维度”，从而设计出合适的搜索框架。

搜索过程中的剪枝，其实就是针对每个“维度”与该维度的边界条件，加以缩放、推导，得出一个相应的不等式，来减少搜索树分支的扩张。例如本题中的剪枝1、剪枝3和剪枝4，就是考虑与半径、高度、体积、表面积这些维度的上下界进行比较后直接得到的。

为了进一步提高剪枝的效果，除了当前花费的“代价”之外，我们还可以对未来至少需要花费的代价进行预算，这样更容易接近每个维度的上下界。例如本题中的前 $dep - 1$ 层最小体积、最小侧面积就是这种想法。剪枝5则通过表面积与体积之间的关系，对不等式进行缩放， $2(n - v) / r[dep]$ 这个式子也是对前 $dep - 1$ 层侧面积的一个估计。这告诉我们在一般的剪枝不足以应对问题的时候，也可以结合各维度之间的联系得到更加精准的剪枝。在A*算法中，我们会更详细地讲解这种“未来预算”理论。

*【例题】Sudoku POJ3076

在上一节中，我们解决了 $9 * 9$ 的传统数独问题。在这道题目中，你需要填写一个 $16 * 16$ 的数独，使得每行、每列、每个 $4 * 4$ 的十六宫格内字母 A~P 均恰好出现一次。

在上一节99的数独问题中，我们只使用了"优先选择能填的数字最少的位置"这一策略，并且只有当某个位置无法填数时才判定失败进行回溯。不过，请读者考虑下面这个1616数独的局部情况：

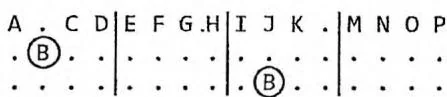
如上图所示，虽然每个位置都还有能填的数，但是因为图中圈出的两个 $B$ 的影响，导致 $B$ 不可能填入第一行中的任何一个空位。类似的还有其他更加复杂的情况。也就是说，我们需要对数独进行更加全面的可行性判定，尽早发现无解的分支执行回溯。

我们加入以下的可行性剪枝：

1. 遍历当前所有的空格

(1) 若某个位置 $\mathrm{A} \sim \mathrm{P}$ 都不能填，立即回溯。
(2) 若某个位置只有 1 个字母可填, 立即填上这个字母。

1. 考虑所有的行

(1) 若某个字母不能填在该行的任何一个空位上，立即回溯。
(2) 若某个字母只能填在该行的某一个空位上，立即填写。

1. 考虑所有的列，执行与第2步类似的过程。

2. 考虑所有的十六宫格，执行类似的过程。

之后，我们再选择可填的字母最少的位置，枚举填写哪个字母作为分支。

使用位运算来进行常数优化仍然是必要的。不过，因为上述剪枝较为复杂，按照上

一节中 $9*9$ 数独的位运算记录方法，实现起来比较困难，所以在本题中，我们直接对每个位置保存一个16位二进制数，存储该位置能填的数字情况，一共 $16*16 = 256$ 个这样的二进制数。在每次递归前，我们简单地把这256个数的副本记录在局部变量上，在还原现场时直接恢复即可。本书配套光盘中提供了本题的参考代码。

数独可以转化为精确覆盖问题，使用一种叫做Dancing Links的数据结构求解。这超出了我们的讨论范围，学有余力的读者可以自行查阅相关资料。不过，建议读者还是使用搜索算法实现上一节与本节中的共计三道数独问题，因为算法思维能力的训练远比学习几个能直接拿来解决问题的数据结构重要。