0x5C_计数类DP
0x5C计数类DP
在本章的最后两节,我们通过几道例题来介绍动态规划中的计数问题和数位统计问题。这两类问题都特别强调“不重不漏”,统计对象的可能情况一般比较多,通常需要精确的划分和整体性的计算。因此,使用动态规划抽象出问题中的“子结构”和推导的“阶段”,将有助于我们准确而高效地进行求解。
【例题】Gerald and Giant Chess Codeforces559C
给定一个 的棋盘,棋盘上只有 个格子是黑色的,其他格子都是白色的。
在棋盘左上角有一个卒,每一步可以向右或向下移动一格,并且不能移动到黑色格子中。求这个卒从左上角移动到右下角,一共有多少种可能的路线。
。输出对 取模后的结果即可。
棋盘上的白色格子数量巨大,而黑色格子最多只有2000个。我们应该考虑如何依靠黑色格子进行计数。如果这个卒能走进黑色格子,那么从左上角走到右下角的路线总数就是 ,我们在0x37节“组合计数”中提到过这个公式。若我们再求出从左上角到右下角经过了至少一个黑色格子的路线数量,二者相减就得到了只经过白色格子的路线数。
把所有黑色格子按照行、列坐标递增的顺序排序。特别地,我们假设左上角是第0个黑色格子,右下角是第 个黑色格子。设第 个黑色格子在第 行第 列。设 表示从左上角走到排序后的第 个黑色格子,并且途中不经过其他黑色格子的路线数。
上式的含义是,枚举 作为从左上角到 经过的第一个黑色格子。也就是从左上角到 不能经过其他黑格子,路线数为 。从 到 随便走,路线数就是一个组合数。等式中求和符号的部分求出了从左上角到 ,途中经过至少一个黑色格子的路线数,用总数减掉,就得到了 。
我们为什么这样设计状态转移方程?为什么限制 作为经过的第一个黑色格子呢?请读者回顾0x53节“区间DP”中的“金字塔”一题,在该题中我们提到,一个状态划分成的若干个子问题之间应该具有互斥性,才不会造成重复统计。实际上,我们在求解计数类动态规划问题时,通常要找到一个“基准点”,围绕这个基准点构造一个不可划分的“整体”,以避免子问题之间的重叠。既然需要求出从左上角到 途中经过至少一个黑色格子的路线数,就枚举第一个经过的黑色格子 ,使左上角到 构成一个整体,让这段路程只能经过白色格子,不能再进行拆分。因为第一个经过的黑色格子不同,所以不同的 对应的路线肯定不会重复。而 又取遍了 之前的所有黑色格子,所以路线也不会遗漏。结合乘法原理和加法原理,我们就得到了状态转移方程中求和符号的部分。
以 为初值,计算上面的状态转移方程,最终 就是本题的答案。对于组合数,可以预处理阶乘关于 的乘法逆元来计算。
define x first
define y second
const int SIZE $= 2010$
pair<int, int> a[SIZE];
int h, w, n, f[SIZE], mod $= 100000007$
long long jc[200010], jcinv[200010];
int C(int n, int m) { return jc[n] \* jcinv[m] % mod \* jcinv[n - m] % mod; }
long long power(long long a, int b) { long.long c = 1; for ( ; b; b >= 1 ) { if (b & 1) c = c*a%mod; a = a*a%mod; } return c;
}
int main() { jc[0] $= 1$ , jcinv[0] $= 1$ . for (int i = 1; i <= 200000; i++) { jc[i] $=$ jc[i - 1] \* i % mod; jcinv[i] $=$ power(jc[i], mod - 2); } cin >> h >> w >> n; for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].x, &a[i].y); sort(a + 1, a + n + 1); a[n + 1].x = h, a[n + 1].y = w; for (int i = 1; i <= n + 1; i++) { f[i] $=$ C(a[i].x + a[i].y - 2, a[i].x - 1); for (int j = 1; j < i; j++) { if (a[j].x > a[i].x || a[j].y > a[i].y) continue; f[i] $=$ (f[i] - (long long)f[j] * C(a[i].x + a[i].y - a[j].x - a[j].y, a[i].x - a[j].x)) % mod; }}cout $\ll$ (f[n + 1] $^+$ mod $\%$ mod<<endl;【例题】Connected Graph POJ1737
求 个节点的无向连通图有多少个,节点有标号,编号为 。
注:节点有标号,意味着下列三种是不同的连通图,都应该算作一次计数。
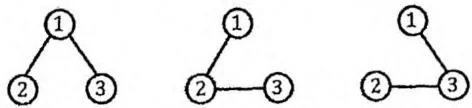
在计数类动态规划中,通常要把一个问题划分成若干个子问题,以便于执行递推。一个连通图不容易进行划分,而一个不连通的无向图则很容易划分成节点更少的两部分。所以我们可以考虑求出 个点的无向图总数,减去 个点的不连通无向图的数量,就是 个点的连通无向图个数。
个点的无向图总数显然是 。含义是 个点的无向图至多有 条边,每条边可有可无,所以共有 张不同的无向图。
接下来计算 个点的不连通无向图的数量。一张不连通的无向图必定由若干个连通块构成。根据上一题提到的“围绕基准点构造一个整体”的思想,我们可以枚举标号为1的节点所在的连通块包含的节点个数 ,从 这 个节点中选出 个,与1号节点一起构成大小为 的连通块。显然,我们有 种选法。剩余 个节点构成任意无向图,有 种方法。
综上所述,设 表示i个节点的无向连通图个数,状态转移方程为:
初值: 。目标:
*【例题】How many of them
在无向连通图中,若一条边被删除后,图会分成不连通的两部分,则称该边为割边。求满足如下条件的无向连通图的数量:
由 个节点构成,节点有标号,编号为 。
割边不超过 条。
3.没有自环和重边。
数据范围: 。答案可能很大,你只需要输出对给定整数 取模后的结果。
在0x66节,我们会详细介绍有关无向图连通性的知识,不熟悉的读者可以简单浏览,或者先记住以下定义和结论:
在无向图中,不含割边的极大连通子图称为双连通分量。若把每个双连通分量看作一个节点,则所有双连通分量和割边构成一个树形结构。如右图所示。
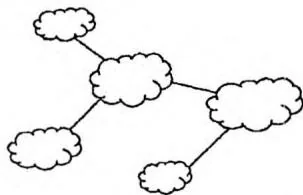
设 表示 个点构成的包含 条割边的无向连通图数量。先来考虑 时的计算方法。
我们多次提到计数类 DP 中“围绕基准点构造一个整体”的思想。在上面的结构中,就以编号为 1 的节点为“基准点”,枚举 1 号节点所在的双连通分量的大小 。从 这 个节点中选出 个,与 1 号节点共同构成双连通分量,方案数为 。
接下来考虑图中其他部分。如果去掉1号节点所在的双连通分量,那么无向图会分成若干个连通块,从每个连通块出发,都有一条边连接到1号节点所在的双连通分量上。例如右图中有3个连通块。
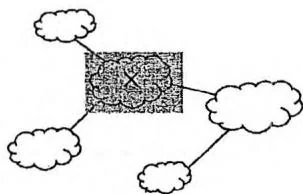
设 表示 个点构成的、有 个连通块的、包含 条割边的无向图数量。
回到 的计算。去掉 1 号节点所在的双连通分量后,图中剩余部分的方案数就是 ,其中 是一个正整数,表示图中剩余部分分为 个连通块。每个连通块与 1 号节点所在的双连通分量之间的边都是一条割边,所以剩余部分还需要贡献 条割边。因为 1 号节点所在的双连通分量包含 个节点,每个连通块可以连接到这 个节点中的任意一个上,所以连接方案共有 种。
综上所述,我们得到 的状态转移方程:
特别地,设 表示 个节点的无向连通图数量,在上一题中我们求出了 ,于是:
最后,我们考虑 的计算方法。以编号最小的节点所在的连通块为基准,枚举该连通块的大小 和割边数量 。当然,需要从 个节点中再选出 个节点构成这个连通块,所以该连通块的方案就有 种。另外,我们需要从
该连通块中选出一个节点,用于与刚才删掉的双连通分量相连,显然有 种选法。除此之外,图中其他部分的方案数就是 。于是,我们得到状态转移方程:
在具体实现时,还要注意一些初值和边界问题,这里就不再赘述。本题较为复杂,供学有余力的读者思考。
【例题】A Decorative Fence POJ1037
有 块长方形的木板,长度分别为 ,宽度都是1。现在要用这 块木板组成一个宽度为 的栅栏,满足在栅栏中,每块木板两侧的木板要么都比它高,要么都比它低。也就是说,栅栏中的木板是高低交错的。我们称“两侧比它低的木板”处于高位,“两侧比它高的木板”处于低位。
显然,有很多种构建栅栏的方案。每个方案可以写作一个长度为 的序列,序列中的各元素是木板的长度。把这些序列按照字典序排序,如下图所示,就是 时所有满足条件的栅栏按照木板长度的字典序排序后的结果。

All cute fences made of planks, ordered by their catalogue numbers.
现在给定整数 ,求排名为 的栅栏中,各木板的长度从左到右依次是多少。 。
类似于倍增优化DP中的“拼凑”思想,我们可以用“试填法”来确定排名为 的栅栏中各木板的长度。具体来说,我们可以从小到大枚举第一块木板的长度,当第一块木板长度为 时,设后面 块木板构成栅栏的方案数为 ,若 ,则说明第一块木板的长度就应该是 ,可以继续尝试确定第二块木板的长度。否则,说明第一块木板应该更长,此时令 减去 , 增加1,重复上述判断。为了让“试填法”更加高效,我们需要预处理 的值。
设 表示用 块长度不同的木板构成栅栏,其中最左边的木板的长度从小到大排在第 位,并且位置状况为 ( 表示处于低位, 表示处于高位)的方案总数。状态转移方程为:
注意,在动态规划的状态表示中,我们没有采取像“用长度为 的木板、最左边的长度为 ”这种长度绝对确定的表述,而是把 和 依据相对大小顺序进行定义。这是因为以下两个子问题其实是等价的:
用长度为 的木板构成栅栏,其中最左边的长度为 。
用 块长度不同的木板构成栅栏,其中最左边的长度排名为 。
实际上我们之前多次使用的“离散化”思想,就与上面这种“等效代换”思想的本质是相同的。利用上面两个子问题的等价性,我们在进行状态转移、数量统计时会非常容易。
在完成动态规划预处理后,就可以执行“试填法”了。
假设已经确定了从左到右前 块木板的长度,现在正在考虑第 块木板。记录上一块木板的长度last、上一块木板的高低位置情况 表示低位, 表示高位)。
把 赋值为 ,即可得到第 块木板应该处于高位还是低位。
特别地,第1块木板既可能处于高位,也可能处于低位。所以要注意单独处理,先确定下来第1块木板的高度和位置情况,作为last和 的初始值。
从小到大枚举第 块木板的长度,设它的真实长度为len,该长度在剩余木板中从小到大排名为 。若 为0,需要满足len<last,否则应满足len>last。
若 ,则令 减掉 ,继续尝试更大的 。
否则,第 块木板的长度就应该是len,可以把它输出。然后,令 增加1,考虑下一块木板。
最后,我们就得到了所求的栅栏方案。动态规划的时间复杂度为 ,试填过程的时间复杂度为 。
int t, n; long long m, f[21][21][2];
void prework() {
f[1][1][0] = f[1][1][1] = 1;
for (int i = 2; i <= 20; i++)
for (int j = 1; j <= i; j++) {
for (int p = j; p <= i - 1; p++)
f[i][j][0] += f[i - 1][p][1];
for (int p = 1; p <= j - 1; p++)
f[i][j][1] += f[i - 1][p][0];
}
}int main(){ prework(); cin>>t; while $(\mathrm{t - - })$ { cin>>n>>m; bool used[21]; memset(used,0,sizeof(used)); int last,k; //第1块木板,既可能处于高位,也可能处于低位,单独处理 for(intj=1;j<=n;j++){ if(f[n][j][1] >= m){ last=j,k=1; break;} else m $=$ f[n][j][1]; if(f[n][j][0] >= m){ last=j,k=0; break;} else m $=$ f[n][j][0]; } used,last]=1; printf("%d",last); //第2~n块木板,高低位置、合法的长度范围与上一块木板有关 for(inti=2;i<=n;i++){ k^=1; //真实长度为len,在剩余木板中排名为j int j=0; for(intlen=1;len<=n;len++){ if(used[len])continue; j++; if(k==0&&len<last||k==1&&len>last){ if(f[n-i+1][j][k]>=m){ last=len; break;} } else m $=$ f[n-i+1][j][k];} used(last] $= 1$ printf("%d",last); } puts("");
}