0x6A_网络流初步
0x6A 网络流初步
网络流是图论中一个博大精深的分支。若要详细讲解网络流的各种模型与应用,甚至可以单独占用一章的篇幅。本节主要希望读者建立对网络流的初步认识,内容会比较浅显,少部分算法和证明的细节会被省略。
一个网络 是一张有向图,图中每条有向边 都有一个给定的权值 ,称为边的容量。特别地,若 ,则 。图中还有两个指定的特殊节点 和 ( ),分别称为源点和汇点。
设 是定义在节点二元组 上的实数函数,且满足:
称为网络的流函数。对于 , 称为边的流量, 称为边的剩余容量。
称为整个网络的流量(其中 表示源点)。
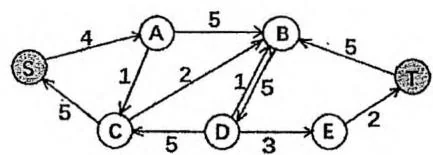
如下图所示。左边是一个网络,有源点 、汇点 以及 共7个点。有向边上的数值标识了边的容量,例如 。
右边画出了该网络的一个流,在有向边上用“ ”的形式标注流量,例如 。流量为0的边省略了标注。值得一提的是,按照流函数的定义,图中标注的每条边的反向边其实都有一个负的流量,例如 , ,这些没有标出,请读者留意。
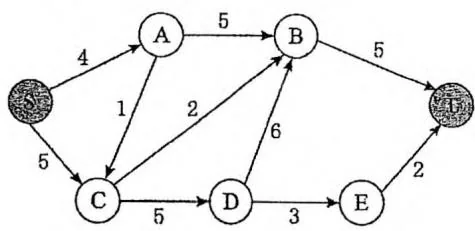
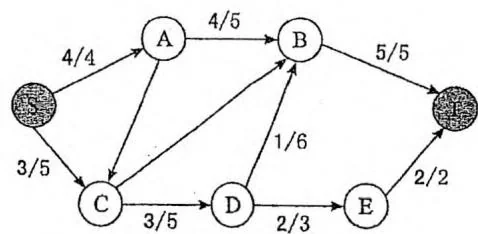
上文给出的流函数 的三条性质分别称为容量限制、斜对称和流量守恒。尤其是流量守恒定律,它告诉我们网络中除源点、汇点以外,任何节点不储存流,其流入总量等于流出总量。网络流模型可以形象地描述为:在不超过容量限制的前提下,“流”从源点源源不断地产生,流经整个网络,最终全部归于汇点。
最大流
对于一个给定的网络,合法的流函数 有很多。使得整个网络的流量 最大(其中 表示源点)的流函数被称为网络的最大流,此时的流量被称为网络的最大流量。
最大流能解决许多实际的问题。就拿我们上两节讨论的二分图为例。对于一张 个点 条边的二分图,我们可以新增一个源点 和一个汇点 ,从 到每个左部点连有向边,从每个右部点到 连有向边,把原二分图的每条边看作从左部点到右部点的有向边,形成一张 个点 条边的网络,网络中每条边的容量都设为1,如下图所示。容易发现,二分图的最大匹配数就等于网络的最大流量,求出最大流后,所有有流经过的点、边就是匹配点、匹配边。
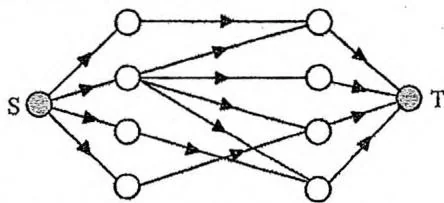
进一步地,若要求二分图多重匹配,则只需把 到左部点的有向边容量设为左部点的匹配数量上限 ,右部点到 的有向边容量设为右部点的匹配数量上限 ,原二分图每条边的容量设为 ,再求最大流即可。
计算最大流的算法很多,本节简单涉及Edmonds-Karp增广路算法和Dinic算法。
Edmonds-Karp 增广路算法
若一条从源点 到汇点 的路径上各条边的剩余容量都大于 0,则称这条路径为一条增广路。显然,可以让一股流沿着增广路从 流到 ,使网络的流量增大。Edmonds-Karp 算法的思想就是不断用 BFS 寻找增广路,直至网络上不存在增广路为止。
在每轮寻找增广路的过程中,Edmonds-Karp算法只考虑图中所有 的边,用BFS找到任意一条从 到 的路径,同时计算出路径上各边的剩余容量的最小值 ,则网络的流量就可以增加 。
需要注意的是,当一条边的流量 时,根据斜对称性质,它的反向边流量 ,此时必定有 。故Edmonds-Karp算法在BFS时除了
原图的边集 之外,还应该考虑遍历 中每条边的反向边。
在具体实现时,我们可以按照邻接表“成对存储”技巧(在之前的章节曾多次提及),把网络的每条有向边及其反向边存在邻接表下标为“2和3”“4和5”“6和7”……的位置上,每条边只记录剩余容量 即可。当一条边 流过大小为 的流时,令 的剩余容量减小 , 的剩余容量增大 。
如下图所示。第一幅图是网络中每条边的原始容量,Edmonds-Karp算法找到了流量为5的增广路 。于是在第二幅图中,剩余容量对应发生了变化。紧接着,第三幅图中,算法又找到了流量为2的增广路 。最终在第四幅图中,网络不存在增广路,最大流的大小就是7。图中省略了剩余容量为0的边。
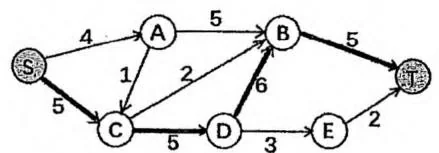
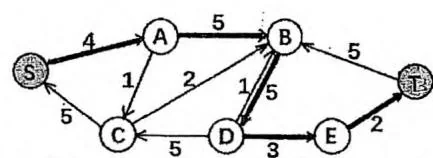
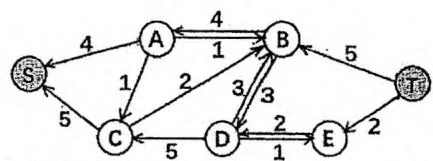
Edmonds-Karp 增广路算法的时间复杂度为 。然而在实际运用中则远远达不到这个上界,效率较高,一般能够处理 规模的网络。
const int inf = 1 << 29, N = 2010, M = 20010;
int head[N], ver[M], edge[M], Next[M], v[N], incf[N], pre[N];
int n, m, s, t, tot, maxflow;
void add(int x, int y, int z) {
ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot;
ver[++tot] = x, edge[tot] = 0, Next[tot] = head[y], head[y] = tot;
}bool bfs(){memset(v,0,sizeof(v)); queue<int>q; q.push(s); $v[s] = 1$ incf[s] $\equiv$ inf; //增广路上各边的最小剩余容量while (q.size()) { int x = q.front(); q.pop(); for (int i = head[x]; i; i = Next[i]) if (edge[i]) { int y = ver[i]; if (v[y]) continue; incf[y] = min(incf[x], edge[i]); pre[y] = i; // 记录前驱,便于找到最长路的实际方案 q.push(y), v[y] = 1; if (y == t) return 1; } return 0;
}
void update() { // 更新增广路及其反向边的剩余容量 int x = t; while (x != s) { int i = pre[x]; edge[i] -= incf[t]; edge[i^1] += incf[t]; // 利用“成对存储”的xor1技巧 x = ver[i^1]; } maxflow += incf[t];
}
int main() { while (cin >> m >> n) { memset(head, 0, sizeof(head)); s = 1, t = n; tot = 1; maxflow = 0; for (int i = 1; i <= m; i++) { int x, y, c; scanf("%d%d%d", &x, &y, &c); add(x, y, c); } while (bfs()) update(); cout << maxflow << endl; }Dinic算法
在任意时刻,网络中所有节点以及剩余容量大于0的边构成的子图被称为残量网络。Edmonds-Karp每轮可能会遍历整个残量网络,但只找出1条增广路,还有进一步优化的空间。
在 节介绍宽度优先遍历时,我们就提到了节点的层次 ,它表示 到 最少需要经过的边数。在残量网络中,满足 的边 构成的子图被称为分层图。分层图显然是一张有向无环图。
Dinic算法不断重复以下步骤,直到在残量网络中 不能到达
在残量网络上BFS求出节点的层次,构造分层图。
在分层图上DFS寻找增广路,在回溯时实时更新剩余容量。另外,每个点可以流向多条出边,同时还加入了若干剪枝,请参阅参考程序及其注释。
Dinic算法的时间复杂度为 。实际运用中远远达不到这个上界,可以说是比较容易实现的效率最高的网络流算法之一,一般能够处理 规模的网络。特别地,Dinic算法求解二分图最大匹配的时间复杂度为 ,实际表现则更快。
const int inf = 1 << 29, N = 50010, M = 300010;
int head[N], ver[M], edge[M], Next[M], d[N];
int n, m, s, t, tot, maxflow;
queue<int> q;
void add(int x, int y, int z) {
ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot;
ver[++tot] = x, edge[tot] = 0, Next[tot] = head[y], head[y] = tot;
}
bool BFS() { // 在残量网络上构造分层图
memset(d, 0, sizeof(d));
while (q.size()) q.pop();
q.push(s); d[s] = 1;
while (q.size()) {
int x = q.front(); q.pop();
for (int i = head[x]; i; i = Next[i])
if (edge[i] && !d[ver[i]]) {
q.push(ver[i]);
d[ver[i]] = d[x] + 1;
if (ver[i] == t) return 1;
}
}return 0;
}
int dinic(int x, int flow) { // 在当前分层图上增广 if $(x == t)$ return flow; int rest $=$ flow,k; for (int i = head[x]; i && rest; i = Next[i]) if (edge[i] && d[ver[i]] $= =$ d[x] + 1) { k = dinic( ver[i], min(rest, edge[i])); if (!k) d[ver[i]] = 0; // 剪枝,去掉增广完毕的点 edge[i] -- k; edge[i ^ 1] += k; rest $= = k;$ } return flow - rest;
}
int main() { cin >> n >> m; cin >> s >> t; // 源点、汇点 tot $= 1$ ; for (int i = 1; i <= m; i++) { int x,y,c; scanf("%d%d%d", &x,&y,&c); add(x,y,c); } int flow $= 0$ while (bfs()) while (flow = dinic(s, inf)) maxflow $+ =$ flow; cout << maxflow << endl;二分图最大匹配的必须边与可行边
给定一张二分图,其最大匹配的方案不一定是唯一的。若任何一个最大匹配方案的匹配边都包括 ,则称 为二分图最大匹配的必须边。若 至少属于一个最大匹配的方案,则称 为二分图最大匹配的可行边。
先来考虑一种简化情况——二分图的最大匹配是一组完备匹配。我们先任意求出一组完备匹配的方案,此时左、右部所有的节点都是匹配点。
根据定义, 是必须边,当且仅当以下两个条件都满足:
当前是匹配边。
删除边 后,不能找到另一条从 到 的增广路。
是可行边,当且仅当满足以下两个条件之一:
当前是匹配边。
是非匹配边,设当前 与 匹配, 与 匹配,连接边 后,节点 失去匹配。必须能找到一条从 到 的增广路。
如果我们把二分图 中的“非匹配边”看作从左部到右部的有向边,把“匹配边”看作从右部到左部的有向边,构成一张新的有向图,记为 ,那么 中从 到 有增广路,等价于 中存在从 到 的路径。
考虑必须边的条件, 是匹配边,对应 中有一条从 到 的有向边。在此前提下,若 到 还存在一条路径,则 和 互相可达,必处于同一个强连通分量中。如下图所示, 和 在 中互相可达,构成一个环,把环上的边的匹配状态取反,得到另一组完备匹配。
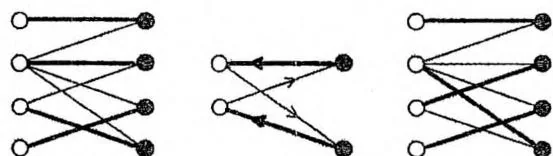
因此,必须边的判定条件可改写为: 当前是二分图 的匹配边,并且 两点在有向图 中属于不同的强连通分量。
类似地,可行边的判定条件可改写为: 当前是二分图 的匹配边,或者 两点在有向图 中属于同一个强连通分量。
【例题】舞动的夜晚 ContestHunter#17-C
L公司和H公司举办了一次联谊晚会。晚会上,L公司的N位员工和H公司的M位员工打算进行一场交际舞会。在这些领导中,一些L公司的员工和H公司的员工之间是互相认识的,这样的认识关系一共有E对。舞会上,每位员工会尝试选择一名他认识的对方公司的员工作为舞伴,并且每位员工至多跳一支舞。完成的交际舞的数量越多,晚会的气氛就越热烈。顾及晚会的气氛,员工们希望知道,哪些员工之间如果进行了交际舞,就会使整场晚会能够完成的交际舞的最大数量减小。
数据范围: , 。
本题是让我们求二分图的不可行边(可行边的补集)。不过,本题不保证二分图的最大匹配是一组完备匹配。
在这种情况下,必须边、可行边的第二个条件会出现问题。设 是非匹配边:
二者之一可能本来就是非匹配点。不妨设 是非匹配点,此时直接断开 原来的匹配边,连接 ,得到的匹配集仍然是最大匹配。
即使当前 与 匹配, 与 匹配,连接边 后,节点 失去匹配,我们也不一定非要找到从 到 的增广路。因为从 出发找到到达另一个非匹配点 的增广路,同样可以得到一组包含 的最大匹配。
所以我们不能像完备匹配中一样,直接用强连通分量进行判定。然而,我们可以借助网络流的源点和汇点。回想我们根据二分图 建立有向图 的方法, 其实就是用网络流计算二分图最大匹配时,残量网络中除去源点、汇点之外的部分——非匹配边(左部到右部)的剩余容量为 1,匹配边的反向边(右部到左部)的剩余容量为 1。
若 当前是非匹配点,则 的剩余容量必定为 1。若 当前是匹配点,则 的剩余容量必定为 0, 的剩余容量必定为 1。换言之,残量网络中存在路径 。若二分图中 到 有增广路,则残量网络上 能到达 ,进而到达 。故 仍在同一个强连通分量中,它们借助汇点 实现了连通。
综上所述,在一般的二分图中(最大匹配不一定是完备匹配),可以用最大流计算出任意一组最大匹配。此时必须边的判定条件为: 流量为 1,并且在残量网络上属于不同的强连通分量。可行边的判定条件为: 流量为 1,或者在残量网络上属于同一个强连通分量。
使用Dinic算法求最大流,Tarjan算法求强连通分量,最后逐一对边进行判定,整个算法的时间复杂度为
最小割
给定一个网络 ,源点为 ,汇点为 。若一个边集 被删去之后,源点 和汇点 不再连通,则称该边集为网络的割。边的容量之和最小的割称为网络的最小割。
最大流最小割定理
任何一个网络的最大流量等于最小割中边的容量之和,简记为“最大流 最小割”。
假设“最小割 最大流”,那么割去这些边之后,因为网络流量尚未最大化,所以仍然可以找到一条 到 的增广路,与 不连通矛盾,故“最小割 最大流”。如果我们能给出一个“最小割 最大流”的构造方案,即可得到上述定理。
求出最大流后,从源点开始沿残量网络BFS,标记能够到达的点。 中所有连接“已标记点 ”和“未标记点 ”的边 构成该网络的最小割。详细证明略。
【例题】Cable TV Network FOJ1966
给定一张无向图,求最少去掉多少个点,可以使图不连通。点数 。
若无向图不连通,则图中必有两个点不连通,但这两个点是未知的。可以枚举这两个点 和 ,然后求在剩余的 个节点中最少去掉多少个,可以使 和 不连通。当然我们要求 和 不是直接相连的,否则不可能达到要求。在每次枚举的结果中取最小值就是本题的答案。
“去掉最少的点使 不连通”的问题与最小割十分相似,只不过要割的是“点”而不是“边”。我们可以按照下面的方法构建一个网络:
把原来无向图中的每个点 ,拆成 和 两个点。
对 ,连有向边 ,容量为 1。
对于原无向图的每条边 , 在网络中连有向边 , 容量为 。
以 为网络的源点, 为网络的汇点,求最小割(最大流),即可得到最少需要去掉的点数。
在上面的网络中, 这条有向边对应原无向图的节点 。无向图中任意经过点 的路径,对应在网络中必须先到达 ,然后通过 ,再从 离开。我们一般称 为“入点”, 为“出点”。容易发现,在无向图中删去一个点,就等价于在网络中断开 。
另外,我们只能删掉无向图的节点,不能删掉无向图的边,所以网络中其他边的容量都设为 (实际可设为大于 的整数)。最小割必定不会包含这些容量为 的边——因为去掉所有容量为1的边(容量之和为 ),就足以使 和 不连通了。
综上所述,网络的最小割就是由最少数量的形如 的边构成的边集,也就是原图最少需要去掉的点数。
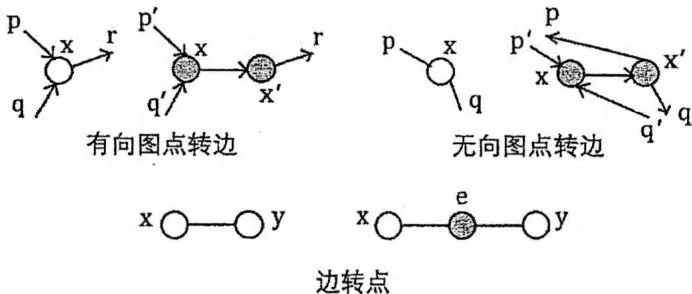
本题的解法包含两个重要的技巧。一是“点边转化”,图的节点可以拆为“入点”和“出点”两个,把点的属性体现在“入点”与“出点”之间的边上;图的边也可以分成两截,在中间加一个节点,把边的属性体现在中间的点上,如下图所示。二是在最小割中,容量为 的边具有“防止割断”的含义。
费用流
给定一个网络 ,每条边 除了有容量限制 ,还有一个给定的“单位费用” 。当边 的流量为 时,就要花费 。该网络中总花费最小的最大流被称为“最小费用最大流”,总花费最大的最大流被称为“最大费用最大流”,二者合称为“费用流”模型。注意:费用流的前提是最大流,然后才考虑费用的最值。
类似于“二分图最大匹配”与最大流的关系,“二分图带权最大匹配”可直接用最大费用最大流求解,每条边的权值就是它的单位费用。
Edmonds-Karp 增广路算法
在Edmonds-Karp求解最大流的基础上,把“用BFS寻找任意一条增广路”改为“用SPFA寻找一条单位费用之和最小的增广路”(也就是把 当做边权,在残量网络上求最短路)即可求出最小费用最大流。注意:一条反向边 的费用应设为 。参考程序将以下面的例题为背景给出。
【例题】K取方格数 FOJ3422
在 节“线性DP”的例题“传纸条”中,我们解决了“二取方格数”问题。 取方格数是它的扩展。在一个 的矩形网格中,每个格子里都写着一个整数。可以从左上角到右下角安排 条路线,每一步只能往下或往右,沿途经过的格子中的整数会被取走。若多条路线重复经过一个格子,只取一次。求能取得的整数的和最大是多少。 。
当 时,若把第 行第 列的格子 看作一个节点,从格子 对应的节点向格子 对应的节点连有向边,则能取得的整数之和的最大值就相当于从 到 的最长路(只不过权值在节点上)。
当 时,我们需要限制“每个节点的权值只能被算一次”。这种点(或边)同时带有权值和上界限制的最优化问题,恰好与费用流的模型非常相似。我们可以按照如下规则构造一个网络:
应用“点边转化”技巧,把每个格子 对应的节点拆成一个“入点”和一个“出点”,整个网络共有 个点。
从每个 的入点向出点连两条有向边。第一条有向边容量为 1,费用为格子 中的数。第二条有向边容量为 ,费用为 0。这表示第一次经过该点时,可以把数取走,之后再经过时就不再计算。
从 的出点到 和 的入点连有向边,容量为 ,费用为
0。
以 (1,1) 的入点为源点, 的出点为汇点,求最大费用最大流。因为 (1,1) 的入点和出点之间的两条有向边一共只有 的容量,并且“费用流”先保证“最大流”,再最优化“费用”,所以最终会恰好找到 条路线。求出的总费用就是本题的答案。
const int N = 5010, M = 200010;
int ver[M], edge[M], cost[M], Next[M], head[N];
int d[N], incf[N], pre[N], v[N];
int n, k, tot, s, t, maxflow, ans;
void add(int x, int y, int z, int c) {
// 正向边,初始容量 z,单位费用 c
ver[++tot] = y, edge[tot] = z, cost[tot] = c;
Next[tot] = head[x], head[x] = tot;
// 反向边,初始容量 0,单位费用 -c,与正向边“成对存储”
ver[++tot] = x, edge[tot] = 0, cost[tot] = -c;
Next[tot] = head[y], head[y] = tot;
}
int num(int i, int j, int k) {
return (i - 1)*n + j + k*n*n;
}
bool spfa() {
queue<int> q;
memset(d, 0xfc, sizeof(d)); // -INF
memset(v, 0, sizeof(v));
q.push(s); d[s] = 0; v[s] = 1; // SPFA 求最长路
incf[s] = 1 << 30; // 增广路上各边的最小剩余容量
while (q.size()) {
int x = q.front(); v[x] = 0; q.pop();
for (int i = head[x]; i; i = Next[i]) {
if (!edge[i])
continue; // 剩余容量为 0,不在残量网络中,不遍历
int y = ver[i];
if (d[y] < d[x] + cost[i]) {
d[y] = d[x] + cost[i];
}
}$\begin{array}{l}\mathrm{incf}[y] = \min (\mathrm{incf}[x],\mathrm{edge}[i]);\\ \mathrm{pre}[y] = i; / /\mathrm{~} / \\ \mathrm{if~(~!v[y])~v[y]~ = ~1,~q.push(y);} \end{array}$
if(!v[y])v[y] $= 1$ ,q.push(y);1
1
1
if(d[t] == 0xcfcfcfcf) return false; //汇点不可达,已求出最大流return true;// 更新最长增广路及其反向边的剩余容量
void update() { int $\mathbf{x} = \mathbf{t}$ ; while $(\texttt{x} !=\texttt{s})$ { int i $=$ pre[x]; edge[i] $- =$ incf[t]; edge[i^1] $+ =$ incf[t];//利用“成对存储”的xor1技巧 x=ver[i^1]; } maxflow+=incf[t]; ans+=d[t]*incf[t];
}
int main(){ cin>>n>>k; s=1,t=2*n*n; tot=1; //从2开始“成对存储”,2和3是一对,4和5是一对 for(inti=1;i<=n;i++) { intc;scanf("%d",&c); add(num(i,j,0),num(i,j,1),1,c); add(num(i,j,0),num(i,j,1),k-1,0); if(j<n>add(num(i,j,1),num(i,j+1,0),k,0); if(i<n>add(num(i,j,1),num(i+1,j,0),k,0); } while(spfa())update();//计算最大费用最大流 cout<<ans<<endl;