0x46_二叉查找树与平衡树初步

0x46 二叉查找树与平衡树初步

在二叉树中，有两组非常重要的条件，分别是两类数据结构的基础性质。其一是“堆性质”，我们曾在0x17节中提及。二叉堆以及高级数据结构中的所有可合并堆，都满足“堆性质”。其二就是本节即将探讨的“BST性质”，它是二叉查找树(Binary Search Tree)以及所有平衡树的基础。

BST

给定一棵二叉树，树上的每个节点带有一个数值，称为节点的“关键码”。所谓“BST性质”是指，对于树中的任意一个节点：

  1. 该节点的关键码不小于它的左子树中任意节点的关键码。

  2. 该节点的关键码不大于它的右子树中任意节点的关键码。

满足上述性质的二叉树就是一棵“二叉查找树”(BST)。显然，二叉查找树的中序遍历是一个关键码单调递增的节点序列。

BST的建立

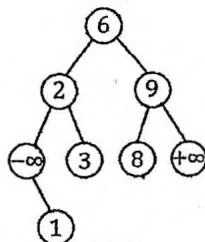
为了避免越界，减少边界情况的特殊判断，我们一般在BST中额外插入一个关键码为正无穷（一个很大的正整数）和一个关键码为负无穷的节点。仅由这两个节点构成的BST就是一棵初始的空BST。如右图所示。

简便起见，在接下来的操作中，我们假设BST不会含有关键码相同的节点。

struct BST {
    int l, r; // 左右子节点在数组中的下标
    int val; // 节点关键码
} a[SIZE]; // 数组模拟链表
int tot, root, INF = 1 << 30;
int New(int val) {
    a[++tot].val = val;
    return tot;
}
void Build() {
    New(-INF), New(INF);
    root = 1, a[1].r = 2;
}

BST的检索

在 BST 中检索是否存在关键码为 val 的节点。

设变量 pp 等于根节点 root，执行以下过程：

  1. 若 pp 的关键码等于 val，则已经找到。

  2. 若 pp 的关键码大于 val

(1) 若 pp 的左子节点为空，则说明不存在 val。

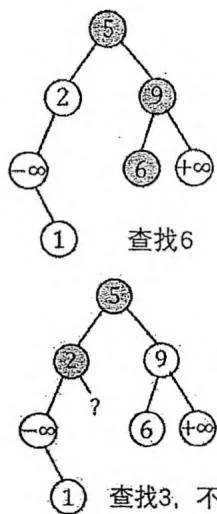
(2) 否则，在 pp 的左子树中递归进行检索。

  1. 若 pp 的关键码小于 val

(1) 若 pp 的右子节点为空，则说明不存在 val。
(2) 否则，在 pp 的右子树中递归进行检索。

int Get(int p, int val) {
    if (p == 0) return 0; // 检索失败
    if (val == a[p].val) return p; // 检索成功
    return val < a[p].val ? Get(a[p].1, val) : Get(a[p].r, val);
}

BST的插入

在 BST 中插入一个新的值 val（假设目前 BST 中不存在关键码为 val 的节点）。

与 BST 的检索过程类似。

在发现要走向的 pp 的子节点为空，说明val不存在时，直接建立关键码为val的新节点作为 pp 的子节点。


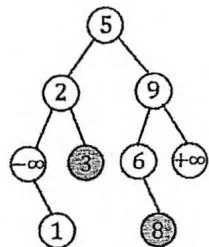
插入3和8

void Insert(int &p, int val) {
    if (p == 0) {
        p = New(val); // 注意 p 是引用，其父节点的 l 或 r 值会被同时更新
        return;
    }
    if (val == a[p].val) return;
    if (val < a[p].val) Insert(a[p].l, val);
    else Insert(a[p].r, val);
}

BST求前驱/后继

以“后继”为例。val 的“后继”指的是在 BST 中关键码大于 val 的前提下，关键码最小的节点。

初始化 ansans 为具有正无穷关键码的那个节点的编号。然后，在 BST 中检索 valval 。在检索过程中，每经过一个节点，都检查该节点的关键码，判断能否更新所求的后继 ansans 。

检索完成后，有3种可能的结果：

  1. 没有找到 val。

此时val的后继就在已经经过的节点中，ans即为所求。

2.找到了关键码为val的节点 pp ，但 P\mathcal{P} 没有右子树。

与上一种情况相同，ans即为所求。

3.找到了关键码为val的节点 pp ，且 P\mathcal{P} 有右子树。

从 pp 的右子节点出发，一直向左走，就找到了val的后继。

intGetNext(intval){ int ans  $= 2$  //a[2].val  $\equiv =$  INF intp  $=$  root; while(p){ if(val  $\equiv =$  a[p].val）{//检索成功 if(a[p].r>0）{//有右子树 p=a[p].r; //右子树上一直向左走 while(a[p].1>0)p=a[p].l; ans  $=$  p; } break; } //每经过一个节点，都尝试更新后继 if(a[p].val  $>$  val&&a[p].val<a[ans].val）ans  $=$  p; p  $=$  val<a[p].val?a[p].l:a[p].r; } return ans;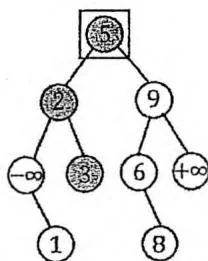


求3的后继


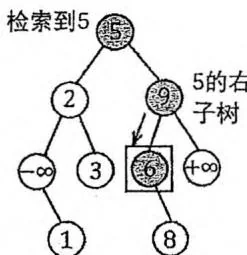
求5的后继

BST的节点删除

从 BST 中删除关键码为 val 的节点。

首先，在 BST 中检索 val，得到节点 pp 。

若 pp 的子节点个数小于 2，则直接删除 pp ，并令 pp 的子节点代替 pp 的位置，与 pp 的父节点相连。

若 pp 既有左子树又有右子树，则在 BST 中求出 val 的后继节点 next。因为 next 没有左子树，所以可以直接删除 next，并令 next 的右子树代替 next 的位置。最后，再让 next 节点代替 pp 节点，删除 pp 即可。如右图所示。


删除5 5的后继6代替5 6的右子树8代替6

void Remove(int val) { //检索val，得到节点p int  $\& p =$  root; while (p){ if(val  $= = a[p].val)$  break;  $\mathsf{p} = \mathsf{val} <   \mathsf{a}[\mathsf{p}].\mathsf{val}$  ?a[p].1:a[p].r; } if  $(p = = 0)$  return; if(a[p].1  $= = 0$  ）{//没有左子树  $\mathsf{p} = \mathsf{a}[\mathsf{p}].\mathsf{r}; / /$  右子树代替p的位置，注意p是引用} elseif(a[p].r  $= = 0$  ）{//没有右子树  $\mathsf{p} = \mathsf{a}[\mathsf{p}].\mathsf{l}; / /$  左子树代替p的位置，注意p是引用} else{//既有左子树又有右子树 //求后继节点 int next  $= a[p].r;$  while(a[next].1>0）next  $=$  a[next].l; //next一定没有左子树，直接删除 Remove(a[next].val); //令节点next代替节点p的位置 a[next].1=a[p].1,a[next].r=a[p].r;  $\mathsf{p} = \mathsf{next}; / /$  注意p是引用 }

在随机数据中，BST一次操作的期望复杂度为 O(log⁡N)O(\log N) 。然而，BST很容易退化，例如在BST中依次插入一个有序序列，将会得到一条链，平均每次操作的复杂度为 O(N)O(N) 。我们称这种左右子树大小相差很大的BST是“不平衡”的。有很多方法可以维持BST的平衡，从而产生了各种平衡树。本节我们介绍一种入门级平衡树——Treap。

Treap

满足 BST 性质且中序遍历为相同序列的二叉查找树是不唯一的。这些二叉查找树是等价的，它们维护的是相同的一组数值。在这些二叉查找树上执行同样的操作，将得到相同的结果。因此，我们可以在维持 BST 性质的基础上，通过改变二叉查找树的形

态，使得树上每个节点的左右子树大小达到平衡，从而使整棵树的深度维持在 O(log⁡N)O(\log N) 级别。

改变形态并保持 BST 性质的方法就是“旋转”。最基本的旋转操作称为“单旋转”，它又分为“左旋”和“右旋”。如下图所示。

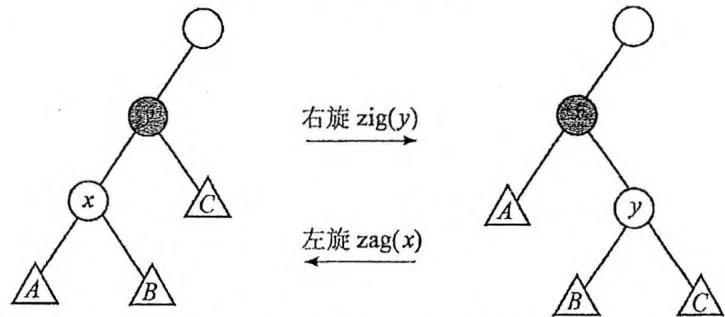
注意：某些书籍中把左、右旋操作定义为一个节点绕其父节点向左或右旋转。本书后面即将讲解的Treap代码仅记录左右子节点，没有记录父节点，为了方便起见，统一以“旋转前处于父节点位置”（旋转后处于子节点位置）的节点作为左、右旋的作用对象（函数参数）。

以右旋为例。在初始情况下， xx 是 yy 的左子节点， AA 和 BB 分别是 xx 的左右子树， CC 是 yy 的右子树。

“右旋”操作在保持BST性质的基础上，把 xx 变为 yy 的父节点。因为 xx 的关键码小于 yy 的关键码，所以 yy 应该作为 xx 的右子节点。

当 xx 变成 yy 的父节点后， yy 的左子树就空了出来，于是 xx 原来的右子树 BB 就恰好作为 yy 的左子树。

右旋操作的代码如下， zig⁡(p)\operatorname{zig}(p) 可以理解成把 pp 的左子节点绕着 pp 向右旋转：

void zig(int &p) {
    int q = a[p].l;
    a[p].l = a[q].r, a[q].r = p;
    p = q; // 注意 p 是引用
}

左旋操作的代码如下， zag⁡(p)\operatorname{zag}(p) 可以理解成把 pp 的右子节点绕着 pp 向左旋转：

void zag(int &p) {
    int q = a[p].r;
    a[p].r = a[q].l, a[q].l = p;
    p = q; // 注意 p 是引用
}

合理的旋转操作可使 BST 变得更“平衡”。如下页图所示，对形态为一条链的 BST

进行一系列单旋转操作后，这棵BST变得比较平衡了。

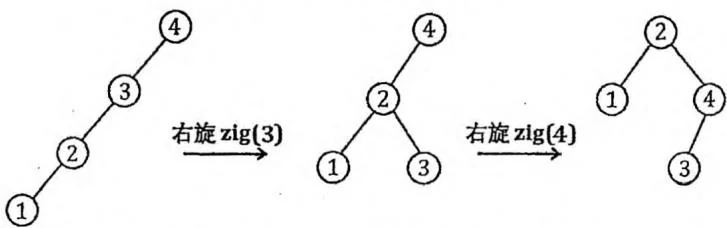
现在，我们的问题是，怎样才算“合理”的旋转操作呢？我们发现，在随机数据下，普通的BST就是趋近平衡的。Treap的思想就是利用“随机”来创造平衡条件。因为在旋转过程中必须维持BST性质，所以Treap就把“随机”作用在堆性质上。

Treap 是英文 Tree 和 Heap 的合成词。Treap 在插入每个新节点时，给该节点随机生成一个额外的权值。然后像二叉堆的插入过程一样，自底向上依次检查，当某个节点不满足大根堆性质时，就执行单旋转，使该点与其父节点的关系发生对换。

特别地，对于删除操作，因为 Treap 支持旋转，我们可以直接找到需要删除的节点，并把它向下旋转成叶节点，最后直接删除。这样就避免了采取类似普通 BST 的删除方法可能导致的节点信息更新、堆性质维护等复杂问题。

总而言之，Treap 通过适当的单旋转，在维持节点关键码满足 BST 性质的同时，还使每个节点上随机生成的额外权值满足大根堆性质。Treap 是一种平衡二叉查找树，检索、插入、求前驱后继以及删除节点的时间复杂度都是 O(log⁡N)O(\log N) 。

【例题】普通平衡树 BZOJ3224/TYVJ1728

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入数值 xx

  2. 删除数值 xx (若有多个相同的数，应只删除一个)

  3. 查询数值 xx 的排名 (若有多个相同的数，应输出最小的排名)

  4. 查询排名为 xx 的数值

  5. 求数值 xx 的前驱 (前驱定义为小于 xx 的最大的数)

  6. 求数值 xx 的后继 (后继定义为大于 xx 的最小的数)

这是一道平衡树的模板题，我们直接用Treap实现即可。

根据题意，数据中可能有相同的数值，我们可以给每个节点增加一个域 cnt，记录该节点的“副本数”，初始为 1。若插入已经存在的数值，就直接把“副本数”加 1。在删除时，减少节点的“副本数”，当减为 0 时删除该节点。这样就可以比较容易地处理关键码相同的问题。

题目还要求查询排名，我们可以给每个节点增加一个域 size，记录以该节点为根的子树中所有节点的“副本数”之和。当不存在重复数值时，size 其实就是子树大小。

与线段树一样，我们需要在插入或删除时从下往上更新 size 信息。另外，在发生旋转操作时，也需要同时修改 size。最后，在 BST 检索的基础上，通过判断左、右子树 size 的大小，选择适当的一侧递归，就很容易查询排名了。

因为在插入和删除操作时，Treap 的形态会发生变化，所以我们一般使用递归实现，以便于在回溯时更新 Treap 上存储的 size 等信息。

const int SIZE = 100010;  
struct Treap {  
    int l, r; // 左右子节点在数组中的下标  
    int val, dat; // 节点关键码、权值  
    int cnt, size; // 副本数、子树大小  
} a[SIZE]; // 数组模拟链表  
int tot, root, n, INF = 0x7FFFFFF;  
int New(int val) {  
    a++; val = val;  
    a[tot].dat = rand();  
    a[tot].cnt = a[tot].size = 1;  
    return tot;  
}  
void Update(int p) {  
    a[p].size = a[a[p].l].size + a[a[p].r].size + a[p].cnt;  
}  
void Build() {  
    New(-INF), New(INF);  
    root = 1, a[1].r = 2;  
    Update(root);  
}  
int GetRankByVal(int p, int val) {  
    if (p == 0) return 0;  
    if (val == a[p].val) return a[a[p].l].size + 1;  
    if (val < a[p].val) return GetRankByVal(a[p].l, val);  
    return GetRankByVal(a[p].r, val) + a[a[p].l].size + a[p].cnt;

}

int GetValByRank(int p, int rank) { if  $(p == 0)$  return INF; if (a[a[p].1].size >= rank) return GetValByRank(a[p].1, rank); if (a[a[p].1].size + a[p].cnt >= rank) return a[p].val; return GetValByRank(a[p].r, rank - a[a[p].1].size - a[p].cnt); }   
void zig(int &p) { int q = a[p].1; a[p].1 = a[q].r, a[q].r = p, p = q; Update(a[p].r), Update(p);   
}   
void zag(int &p) { int q = a[p].r; a[p].r = a[q].l, a[q].l = p, p = q; Update(a[p].l), Update(p);   
}   
void Insert(int &p, int val) { if  $(p == 0)$  { p = New(val); return; } if (val == a[p].val) { a[p].cnt++, Update(p); return; } if (val < a[p].val) { Insert(a[p].l, val); if (a[p].dat < a[a[p].l].dat) zig(p); // 不满足堆性质，右旋 } else { Insert(a[p].r, val); if (a[p].dat < a[a[p].r].dat) zag(p); // 不满足堆性质，左旋 }
Update(p);   
}   
int GetPre(int val){ int ans  $= 1$  ;//a[1].val  $\equiv = -\mathrm{INF}$  int p  $=$  root; while (p){ if(val  $= =$  a[p].val）{ if(a[p].1>0）{ p=a[p].1; while(a[p].r>0)p=a[p].r; //左子树上一直向右走 ans  $=$  p; } break; } if(a[p].val  $<$  val&&a[p].val>a[ans].val)ans  $=$  p; p  $=$  val  $<$  a[p].val?a[p].l:a[p].r; } return a[ans].val;   
}   
intGetNext(int val){ int ans  $= 2$  ;//a[2].val  $\equiv = \mathrm{INF}$  int p  $=$  root; while(p){ if(val  $= =$  a[p].val）{ if(a[p].r>0）{ p=a[p].r; while(a[p].1>0)p=a[p].1; //右子树上一直向左走 ans  $=$  p; } break; } if(a[p].val  $>$  val&&a[p].val<a[ans].val)ans  $=$  p; p  $=$  val  $<$  a[p].val?a[p].l:a[p].r; } return a[ans].val;
void Remove(int &p, int val) {
    if (p == 0) return;
    if (val == a[p].val) { // 检索到了 val
        if (a[p].cnt > 1) { // 有重复，减少副本数即可
            a[p].cnt--, Update(p);
            return;
        }
    if (a[p].l || a[p].r) { // 不是叶子节点，向下旋转
        if (a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat)
            zig(p), Remove(a[p].r, val);
        else
            zag(p), Remove(a[p].l, val);
        Update(p);
    }
    else p = 0; // 叶子节点，删除
    return;
} 
val < a[p].val ? Remove(a[p].l, val) : Remove(a[p].r, val); 
Update(p);
} 
int main() {
    Build();
    cin >> n;
    while (n--) {
        int opt, x;
        scanf("%d%d", &opt, &x);
        switch (opt) {
            case 1:
                Insert(root, x);
            break;
        case 2:
            Remove(root, x);
            break;
        case 3:
            printf("%d\n", GetRankByVal(root, x) - 1);
            break;
        case 4:
printf("%d\n", GetValByRank(root, x + 1)); break;   
case 5: printf("%d\n", GetPre(x)); break;   
case 6: printf("%d\n", GetNext(x)); break;   
}   
}

除了 Treap 以外，常见的平衡二叉查找树还有 Splay、红黑树、AVL、SBT、替罪羊树等。其中，C++ STL 的 set、map 等就采用了效率很高的红黑树的一种变体。不过，大多数平衡树因为实现比较复杂，或者应用范围能被其他平衡树替代，在算法竞赛等短时间程序设计中并不常用。在这些平衡树中，Splay（伸展树）灵活多变，应用广泛，能够很方便地支持各种动态的区间操作，是用于解决复杂问题的一个重要的高级数据结构。学有余力的读者可以自行查阅相关资料，并尝试用 Splay 完成本章末尾的一道标有“*”号的练习题。

Previous0x44_分块
Next0x45_点分治