0x41并查集

并查集（Disjoint-Set）是一种可以动态维护若干个不重叠的集合，并支持合并与查询的数据结构。详细地说，并查集包括如下两个基本操作：

1. Get，查询一个元素属于哪一个集合。

2. Merge，把两个集合合并成一个大集合。

为了具体实现并查集这种数据结构，我们首先需要定义集合的表示方法。在并查集中，我们采用“代表元”法，即为每个集合选择一个固定的元素，作为整个集合的“代表”。

其次，我们需要定义归属关系的表示方法。第一种思路是维护一个数组 $f$ ，用 $f[x]$ 保存元素 $x$ 所在集合的“代表”。这种方法可以快速查询元素的归属集合，但在合并时需要修改大量元素的 $f$ 值，效率很低。第二种思路是使用一棵树形结构存储每个集合，树上的每个节点都是一个元素，树根是集合的代表元素。整个并查集实际上是一个森林（若干棵树）。我们仍然可以维护一个数组 $fa$ 来记录这个森林，用 $fa[x]$ 保存 $x$ 的父节点。特别地，令树根的 $fa$ 值为它自己。这样一来，在合并两个集合时，只需连接两个树根（令其中一个树根为另一个树根的子节点，即 $fa[root_1] = root_2$ ）。不过在查询元素的归属时，需要从该元素开始通过 $fa$ 存储的值不断递归访问父节点，直至到达树根。为了提高查询效率，并查集引入了路径压缩与按秩合并两种思想。

路径压缩与按秩合并

读者可能已经注意到，第一种思路（直接用数组 $f$ 保存代表）的查询效率很高，我们不妨考虑把两种思路进行结合。实际上，我们只关心每个集合对应的“树形结构”的根节点是什么，并不关心这棵树的具体形态——这意味着下图中的两棵树是等价的：

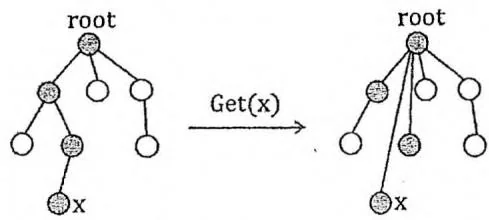
因此，我们可以在每次执行Get操作的同时，把访问过的每个节点（也就是所查询元素的全部祖先）都直接指向树根，即把上图中左边那棵树变成右边那棵。这种优化方法被称为路径压缩。采用路径压缩优化的并查集，每次Get操作的均摊复杂度为 $O(\log N)$ 。

还有一种优化方法被称为按秩合并。所谓“秩”，一般有两种定义。有的资料把并查集中集合的“秩”定义为树的深度（不进行路径压缩）。有的资料把集合的“秩”定义为集合的大小。无论采取哪种定义，我们都可以把集合的“秩”记录在“代表元素”，也就是树根上。在合并时都把“秩”较小的树根作为“秩”较大的树根的子节点。

值得一提的是，当“秩”定义为集合的大小时，“按秩合并”也称为“启发式合并”，它是数据结构相关问题中一种重要的思想，应用非常广泛，不只局限于并查集中。启发式合并的原则是：把“小的结构”合并到“大的结构”中，并且只增加“小的结构”的查询代价。这样一来，把所有结构全部合并起来，增加的总代价不会超过 $N \log N$ 。故单独采用“按秩合并”优化的并查集，每次Get操作的均摊复杂度也是 $O(\log N)$ 。

同时采用“路径压缩”和“按秩合并”优化的并查集，每次Get操作的均摊复杂度可以进一步降低到 $O(\alpha(N))$ ，其中 $\alpha(N)$ 为反阿克曼函数，它是一个比“对数函数” $\log N$ 增长还要慢的函数，对于 $\forall N \leq 2^{2^{10^{19729}}}$ ，都有 $\alpha(N) < 5$ ，故 $\alpha(N)$ 可近似为一个常数。著名计算机科学家R.E.Tarjan于1975年发表的论文中给出了证明。

在实际应用中，我们一般只用路径压缩优化就足够了。接下来，我们对并查集的具体代码实现作一下具体说明。

1. 并查集的存储

使用一个数组 $fa$ 保存父节点（根的父节点设为自己）。

int fa[SIZE];

2. 并查集的初始化

设有 $n$ 个元素，起初所有元素各自构成一个独立的集合，即有 $n$ 棵1个点的树。

for (int i = 1; i <= n; i++) fa[i] = i;

3. 并查集的 Get 操作

若 $x$ 是树根，则 $x$ 就是集合代表，否则递归访问 $f a[x]$ 直至根节点。

int get(int x) { if  $(x == fa[x])$  return x; return fa[x] = get(fa[x]); // 路径压缩，fa直接赋值为代表元素}

4. 并查集的 Merge 操作

合并元素 $x$ 和元素 $y$ 所在的集合，等价于让 $x$ 的树根作为 $y$ 的树根的子节点。

void merge(int x, int y) {
    fa[get(x)] = get(y);
}

【例题】程序自动分析NOI2015/BZOJ4195

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 $x_{1}, x_{2}, x_{3}, \cdots$ 代表程序中出现的变量，给定 $n$ 个形如 $x_{i} = x_{j}$ 或 $x_{i} \neq x_{j}$ 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如一个问题中的约束条件为 $x_{1} = x_{2}, x_{2} = x_{3}, x_{3} = x_{4}, x_{1} \neq x_{4}$ ，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

$1 \leq n \leq 10^{5}, 1 \leq x \leq 10^{9}$ 。

先满足所有“相等”类型的约束条件。容易发现，如果把每个变量看作无向图中的一个节点，每个“相等”的约束条件看作无向图中的一条边，那么两个变量相等当且仅当它们连通。于是，我们可以把变量分成若干个集合，每个集合都对应无向图中的一个连通块。

有两种方法求出这些集合。第一种是建出上面提到的无向图，执行深度优先遍历，划分出无向图中的每个连通块。第二种是使用并查集动态维护。起初，所有变量各自构成一个集合；对于每条“相等”的约束条件，合并它约束的两个变量所在的集合即可。最后，扫描所有“不等”类型的约束条件。若存在一条“不等”的约束条件，它约束的

两个变量处于同一个集合内，则不可能被满足。若不存在这样的“不等”约束，则全部条件可以被满足。

值得注意的是，本题中变量 $x$ 的范围很大。我们可以首先使用0x05节中提到的“离散化”方法把变量 $x$ 的范围映射到 $1 \sim 2n$ 之内，再用上述算法解决。

从这道题目我们看到，并查集能在一张无向图中维护节点之间的连通性，这是它的基本用途之一。实际上，并查集擅长动态维护许多具有传递性的关系。所谓传递性，顾名思义，就是指如果 $A$ 与 $B$ 有某种关系， $B$ 与 $C$ 有某种关系，那么 $A$ 与 $C$ 也有某种确定的关系。本题中的“等于”就是一种传递关系，而“不等于”则显然不具有传递性。

【例题】Supermarket FOJ1456

给定 $N$ 个商品，每个商品有利润 $p_i$ 和过期时间 $d_i$ ，每天只能卖一个商品，过期商品不能再卖，求如何安排每天卖的商品，可以使收益最大。 $1 \leq N, p_i, d_i \leq 10000$ 。

在第 $0 \times 17$ 节中，我们给出了一个利用二叉堆实现的算法。在本节中，请读者尝试换一种思路，使用并查集配合贪心解决本题。

在第 $0 \times 17$ 节的二叉堆做法中，我们把商品按照过期时间从前到后排序，然后依次尝试用每个商品替换掉堆中利润较低的商品。

另一种显而易见的贪心策略则是，优先考虑卖出利润大的商品，并且对每个商品，在它过期之前尽量晚卖出——占用较晚的时间，显然对其他商品具有“决策包容性”。第0x07节曾多次使用这一性质证明过贪心算法。

于是我们可以把商品按照利润从大到小排序，并建立一个关于“天数”的并查集，起初每一天各自构成一个集合。对于每个商品，若它在 $d$ 天之后过期，就在并查集中查询 $d$ 的树根（记为 $r$ ）。若 $r$ 大于0，则把该商品安排在第 $r$ 天卖出，合并 $r$ 与 $r-1$ （令 $r$ 为 $r-1$ 的子节点），答案累加该商品的利润。

这个并查集实际上维护了一个数组中“位置”的占用情况。每个“位置”所在集合的代表就是从它开始往前数第一个空闲的位置（包括它本身）。当一个“位置”被占用时（某一天安排了商品），就把该“位置”在并查集中指向它前一个“位置”。利用并查集的路径压缩，就可以快速找到最晚能卖出的时间（从过期时间往前数第一个空闲的天数）。

$\spadesuit$ “扩展域”与“边带权”的并查集

并查集实际上是由若干棵树构成的森林，我们可以在树中的每条边上记录一个权值，即维护一个数组 $d$ ，用 $d[x]$ 保存节点 $x$ 到父节点 $f a[x]$ 之间的边权。在每次路

径压缩后，每个访问过的节点都会直接指向树根，如果我们同时更新这些节点的 $d$ 值，就可以利用路径压缩过程来统计每个节点到树根之间的路径上的一些信息。这就是所谓“边带权”的并查集。

【例题】银河英雄传说 NOI2002/CODEVS1540

有一个划分成 $N$ 列的星际战场，各列依次编号为 $1,2,\dots ,N$ 。有 $N$ 艘战舰，也依次编号为 $1,2,\dots ,N$ ，其中第 $i$ 号战舰处于第 $i$ 列。

有 $M$ 条指令，每条指令格式为以下两种之一：

1. M $i j$ ，表示让第 $i$ 号战舰所在列的全部战舰保持原有顺序，接在第 $j$ 号战舰所在列的尾部。
   2.Cij，表示询问第 $i$ 号战舰与第 $j$ 号战舰当前是否处于同一列中，如果在同一列中，它们之间间隔了多少艘战舰。

一条“链”也是一棵树，只不过是树的特殊形态。因此可以把每一列战舰看作一个集合，用并查集维护。最初， $N$ 个战舰构成 $N$ 个独立的集合。

在没有路径压缩的情况下， $fa[x]$ 就表示排在第 $x$ 号战舰前面的那个战舰的编号。一个集合的代表就是位于最前边的战舰。另外，让树上每条边带权值 1，这样树上两点之间的距离减 1 就是二者之间间隔的战舰数量。

在考虑路径压缩的情况下，我们额外建立一个数组 $d, d[x]$ 记录战舰 $x$ 与 $f a[x]$ 之间的边的权值。在路径压缩把 $x$ 直接指向树根的同时，我们把 $d[x]$ 更新为从 $x$ 到树根的路径上的所有边权之和。下面的代码对Get函数稍加修改，即可实现对 $d$ 数组的维护：

int get(int x) { if  $(x == fa[x])$  return x; int root = get(fa[x]); // 递归计算集合代表  $d[x] += d[fa[x]]$ ; // 维护d数组——对边权求和 return fa[x] = root; // 路径压缩 }

当接收到一个 $C x y$ 指令时，分别执行 get(x) 和 get(y) 完成查询和路径压缩。若二者的返回值相同，则说明 $x$ 和 $y$ 处于同一列中。因为 $x$ 和 $y$ 此时都已经指向树根，所以 $d[x]$ 保存了位于 $x$ 之前的战舰数量， $d[y]$ 保存了位于 $y$ 之前的战舰数量。二者之差的绝对值再减1，就是 $x$ 和 $y$ 之间间隔的战舰数量。

当接收到一个 $M x y$ 指令时，把 $x$ 的树根作为 $y$ 的树根的子节点，连接的新

边的权值应该设为合并之前集合 $y$ 的大小（根据题意，集合 $y$ 中的全部战舰都排在集合 $x$ 之前）。因此，我们还需要一个 size 数组在每个树根上记录集合大小。下面这段对 Merge 函数稍加修改的代码实现了这条指令：

void merge(int x, int y) {
    x = get(x), y = get(y);
    fa[x] = y, d[x] = size[y];
    size[y] += size[x];
}

刚才我们在“程序自动分析”一题中提到，并查集擅长维护具有传递性的关系及其连通性。在某些问题中，“传递关系”不止一种，并且这些“传递关系”能够互相导出。此时可以使用“扩展域”或者“边带权”的并查集来解决。我们通过几道例题来详细说明。另外，我们会在0x67节探讨2-SAT模型，那时读者就会更加深刻地理解并查集能够处理的“关系”本质。

【例题】 Parity game POJ1733

小A和小B在玩一个游戏。首先，小A写了一个由0和1组成的序列 $S$ ，长度为 $N_{\circ}$

然后，小B向小A提出了M个问题。在每个问题中，小B指定两个数 $l$ 和 $r$ 小A回答 $S[l\sim r]$ 中有奇数个1还是偶数个1。

机智的小B发现小A有可能在撒谎。例如，小A曾经回答过 $S[1\sim 3]$ 中有奇数个1， $S[4\sim 6]$ 中有偶数个1，现在又回答 $S[1\sim 6]$ 中有偶数个1，显然小A是自相矛盾的。请你帮助小B检查这M个答案，并指出在至少多少个回答之后可以确定小A一定在撒谎。即求出一个最小的 $k$ ，使得存在一个01序列满足第 $1\sim k - 1$ 个回答，但不存在满足第 $1\sim k$ 个回答的01序列。 $N \leq 10^{9}$ ， $M <= 10000$ 。

如果我们用sum数组表示序列 $S$ 的前缀和，那么在每个回答中：

1. $S[l \sim r]$ 有偶数个 1，等价于 $sum[l - 1]$ 与 $sum[r]$ 奇偶性相同。

2. $S[l \sim r]$ 有奇数个1，等价于 $sum[l - 1]$ 与 $sum[r]$ 奇偶性不同。

注意，这里没有求出sum数组，我们只是把sum看作变量。读者可以发现，此时本题与本节中“程序自动分析”一题非常类似——都是给定若干个变量和关系，判定这些关系可满足性的问题。不同点是本题的传递关系不止一种：

1. 若 $x_{1}$ 与 $x_{2}$ 奇偶性相同， $x_{2}$ 与 $x_{3}$ 奇偶性也相同，那么 $x_{1}$ 与 $x_{3}$ 奇偶性相同。这种情况与“程序自动分析”中的等于关系一样。

2. 若 $x_{1}$ 与 $x_{2}$ 奇偶性相同， $x_{2}$ 与 $x_{3}$ 奇偶性不同，那么 $x_{1}$ 与 $x_{3}$ 奇偶性不同。

3. 若 $x_{1}$ 与 $x_{2}$ 奇偶性不同， $x_{2}$ 与 $x_{3}$ 奇偶性也不同，那么 $x_{1}$ 与 $x_{3}$ 奇偶性相同。

另外，序列长度 $N$ 很大，但问题数 $M$ 较少，可以先用0x05节中学习的离散化方法把每个问题的两个整数 $l - 1$ 和 $r$ 缩小到等价的 $1\sim 2M$ 以内的范围：

struct { int l, r, ans; } query[10010];
int a[20010], fa[20010], d[20010], n, m, t;
void read_discrete() { // 读入、离散化
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        char str[5];
        scanf("%d%d%s", &query[i].l, &query[i].r, str);
        query[i].ans = (str[0] == 'o' ? 1 : 0);
        a[++t] = query[i].l - 1;
        a[++t] = query[i].r;
    }
    sort(a + 1, a + t + 1);
    n = unique(a + 1, a + t + 1) - a - 1;
}

为了处理本题的多种传递关系，第一种解决方案是使用“边带权”的并查集。

边权 $d[x]$ 为0，表示 $x$ 与 $fa[x]$ 奇偶性相同；为1，表示 $x$ 与 $fa[x]$ 奇偶性不同。在路径压缩时，对 $x$ 到树根路径上的所有边权做异或(xor)运算，即可得到 $x$ 与树根的奇偶性关系。

对于每个问题，设在离散化后 $l - 1$ 和 $r$ 的值分别是 $x$ 和 $y$ ，设ans表示该问题的回答（0代表偶数个，1代表奇数个）。

先检查 $x$ 和 $y$ 是否在同一个集合内（奇偶关系是否已知）。get(x)、get(y) 都执行完成后， $d[x] \lor d[y]$ 即为 $x$ 和 $y$ 的奇偶性关系（如下图）。若 $d[x] \lor d[y] \neq ans$ （该关系与回答矛盾），则在该问题之后即可确定小 A 撒谎。

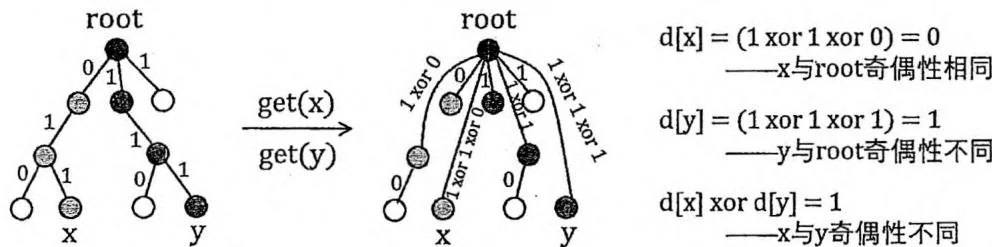
若 $x$ 和 $y$ 不在同一个集合内，则合并两个集合。此时应该先通过 get 操作得到

两个集合的树根（设为 $p$ 和 $q$ ），令 $p$ 为 $q$ 的子节点。如下图所示。已知 $d[x]$ 与 $d[y]$ 分别表示路径 $x \sim p$ 与 $y \sim q$ 之间所有边权的“xor和”， $p \sim q$ 之间的边权 $d[p]$ 是待求的值。显然，路径 $x \sim y$ 由路径 $x \sim p$ ， $p \sim q$ 与 $q \sim y$ 组成，因此 $x$ 与 $y$ 的奇偶性关系 $ans = d[x] \lor d[y] \lor d[y]$ 。进而推出新连接的边权 $d[p] = d[x] \lor d[y] \lor d[ans]$ 。

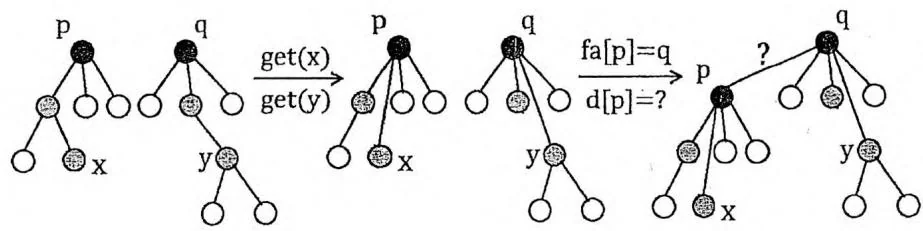
“边带权”并查集解法的主要代码片段：

int get(int x) { if  $(x == fa[x])$  return x; int root  $=$  get(fa[x]);  $d[x]\hat{=} d[fa[x]]$  return fa[x]  $=$  root;   
}   
int main() { read_discrete(); for (int i = 1; i <= n; i++) fa[i]  $= i$  . for (int i = 1; i <= m; i++) { //求出1-1和r离散化之后的值 int  $\mathbf{x} =$  lower_bound(a + 1, a + n + 1, query[i].l - 1) - a; int y  $=$  lower_bound(a + 1, a + n + 1, query[i].r) - a; //执行get函数，得到树根，并进行路径压缩 int p  $=$  get(x), q  $=$  get(y); if  $(p == q)$  { //已经在同一集合内 if  $((d[x]\wedge d[y]) != query[i].ans) / /$  矛盾，输出 {cout << i - 1 << endl; return 0;} } else//不在同一集合，合并 fa[p]  $= q$  ，  $d[p] = d[x]\wedge d[y]\wedge$  query[i].ans; } cout << m << endl; //没有矛盾

第二种解决方案是使用“扩展域”的并查集。

把每个变量 $x$ 拆成两个节点 $x_{odd}$ 和 $x_{even}$ ，其中 $x_{odd}$ 表示 $\text{sum}[x]$ 是奇数， $x_{even}$ 表示 $\text{sum}[x]$ 是偶数。我们也经常把这两个节点称为 $x$ 的“奇数域”和“偶数域”。

对于每个问题，设在离散化后 $l - 1$ 和 $r$ 的值分别是 $x$ 和 $y$ ，设ans表示该问题的回答（0代表偶数个，1代表奇数个）。

1. 若 $ans = 0$ ，则合并 $x_{odd}$ 与 $y_{odd}$ ， $x_{even}$ 与 $y_{even}$ 。这表示“ $x$ 为奇数”与“ $y$ 为奇数”可以互相推出，“ $x$ 为偶数”与“ $y$ 为偶数”也可以互相推出，它们是等价的信息。

2. 若 $ans = 1$ ，则合并 $x_{odd}$ 与 $y_{even}$ ， $x_{even}$ 与 $y_{odd}$ 。这表示“ $x$ 为奇数”与“ $y$ 为偶数”可以互相推出，“ $x$ 为偶数”与“ $y$ 为奇数”也可以互相推出，它们是等价的信息。

上述合并同时还维护了关系的传递性。试想，在处理完 $(x, y, 0)$ 和 $(y, z, 1)$ 两个回答之后， $x$ 和 $z$ 之间的关系也就已知了，如下图所示。这种做法就相当于在无向图上维护节点之间的连通情况，只是扩展了多个域来应对多种传递关系。

在处理每个问题之前，我们当然也要先检查是否存在矛盾。若两个变量 $x$ 和 $y$ 对应的 $x_{odd}$ 和 $y_{odd}$ 节点在同一集合内，则已知二者奇偶性相同。若两个变量 $x$ 和 $y$ 对应的 $x_{odd}$ 和 $y_{even}$ 节点在同一集合内，则已知二者奇偶性不同。

“扩展域”并查集解法的主要代码片段：

int get(int x) { if  $(x == fa[x])$  return x; return fa[x] = get(fa[x]);   
}   
int main() { read_discrete(); for (int i = 1; i <= 2 * n; i++) fa[i] = i; for (int i = 1; i <= m; i++) { // 求出1-1和r离散化之后的值 int x = lower_bound(a + 1, a + n + 1, query[i].1 - 1) - a; int y = lower_bound(a + 1, a + n + 1, query[i].r) - a; int xOdd = x, x_even = x + n;

int yOdd  $= y$  ，y_even  $= y + n$  ·  
if (query[i].ans  $= = 0$  ）{//回答奇偶性相同if（get(xOdd)  $= =$  get(y_even)){//与已知情况矛盾cout<<i-1<<endl;return0;1fa[get(x Odd)]  $= =$  get(y Odd);//合并fa[get(x EVEN)]  $= =$  get(y EVEN);}else{//回答奇偶性不同if（get(x Odd)  $= =$  get(y Odd)){//与已知情况矛盾cout<<i-1<<endl;return0;1fa[get(x Odd)]  $= =$  get(y-even); //合并fa[get(x EVEN)]  $= =$  get(y Odd);1cout<<m<<endl;//没有矛盾

【例题】食物链NOI2001/FOJ1182

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B，B吃C，C吃A。

现有 $N$ 个动物,以 $1 \sim N$ 编号。每个动物都是 $\mathrm{A},\mathrm{B},\mathrm{C}$ 中的一种,但是我们并不知道 它到底是哪一种。有人用两种说法对这 $N$ 个动物所构成的食物链关系进行了描述：

1. 第一种说法是“ $1XY$ ”，表示 $X$ 和 $Y$ 是同类。
   2.第二种说法是“ $2XY$ ”，表示 $X$ 吃 $Y_{\circ}$

此人对 $N$ 个动物，用上述两种说法，一句接一句地说出 $K$ 句话，这 $K$ 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

1. 当前的话与前面的某些真的话冲突，就是假话。

2. 当前的话中 $X$ 或 $Y$ 比 $N$ 大，就是假话。

3. 当前的话表示 $X$ 吃 $X$ , 就是假话。

你的任务是根据给定的 $N(1 \leq N \leq 50000)$ 和 $K$ 句话 $(0 \leq K \leq 10^{5})$ , 输出假话的总数。

本题仍然可以用“边带权”或者“扩展域”的并查集解决。我们以“扩展域”并

查集为例进行讲解。

把每个动物 $x$ 拆成三个节点，同类域 $x_{\text{self}}$ 、捕食域 $x_{\text{eat}}$ 和天敌域 $x_{\text{enemy}}$ 。

若一句话说“ $x$ 与 $y$ 是同类”，则说明“ $x$ 的同类”与“ $y$ 的同类”一样，“ $x$ 捕食的物种”与“ $y$ 捕食的物种”一样，“ $x$ 的天敌”与“ $y$ 的天敌”一样。此时，我们合并 $x_{\text{self}}$ 与 $y_{\text{self}}$ ， $x_{\text{eat}}$ 与 $y_{\text{eat}}$ ， $x_{\text{enemy}}$ 与 $y_{\text{enemy}}$ 。

若一句话说“ $x$ 吃 $y$ ”，说明“ $x$ 捕食的物种”就是“ $y$ 的同类”，“ $x$ 的同类”都是“ $y$ 的天敌”。又因为题目中告诉我们食物链是长度为3的环形，所以“ $x$ 的天敌”就是“ $y$ 捕食的物种”（ $x$ 吃 $y, y$ 吃 $z, z$ 就吃 $x$ ）。此时，应合并 $x_{\text{eat}}$ 与 $y_{\text{self}}$ ， $x_{\text{self}}$ 与 $y_{\text{enemy}}$ ， $x_{\text{enemy}}$ 与 $y_{\text{eat}}$ 。

在处理每句话之前，都要检查这句话的真假。

有两种信息与“ $x$ 与 $y$ 是同类”矛盾：

1. $x_{\text{eat}}$ 与 $y_{\text{self}}$ 在同一集合，说明 $x$ 吃 $y$ 。

2. $x_{\text{self}}$ 与 $y_{\text{eat}}$ 在同一集合，说明 $y$ 吃 $x$ 。

有两种信息与“ $x$ 吃 $y$ ”矛盾：

1. $x_{\text{self}}$ 与 $y_{\text{self}}$ 在同一集合，说明 $x$ 与 $y$ 是同类。

2. $x_{\text{self}}$ 与 $y_{\text{eat}}$ 在同一集合，说明 $y$ 吃 $x$ 。