0x36 组合计数

加法原理

若完成一件事的方法有 $n$ 类，其中第 $i$ 类方法包括 $a_{i}$ 种不同的方法，且这些方法互不重合，则完成这件事共有 $a_{1} + a_{2} + \dots + a_{n}$ 种不同的方法。

乘法原理

若完成一件事需要 $n$ 个步骤，其中第 $i$ 个步骤有 $a_{i}$ 种不同的完成方法，且这些步骤互不干扰，则完成这件事共有 $a_{1} * a_{2} * \dots * a_{n}$ 种不同的方法。

排列数

从 $n$ 个不同元素中依次取出 $m$ 个元素排成一列，产生的不同排列的数量为：

P _ {n} ^ {m} = \frac {n !}{(n - m) !} = n * (n - 1) * \dots * (n - m + 1)

组合数

从 $n$ 个不同元素中取出 $m$ 个组成一个集合(不考虑顺序)，产生的不同集合数量

为：

C _ {n} ^ {m} = \frac {n !}{m ! (n - m) !} = \frac {n * (n - 1) * \cdots * (n - m + 1)}{m * (m - 1) * \cdots * 2 * 1}

性质

$C_n^m = C_n^{n - m}$
$C_n^m = C_{n - 1}^m +C_{n - 1}^{m - 1}$
$C_n^0 + C_n^1 + C_n^2 + \dots + C_n^n = 2^n$

证明：

由组合数的定义，对于从 $n$ 个不同元素中取出 $m$ 个组成的每个集合，剩余未取出的元素也构成一个集合，两个集合一一对应，所以性质1成立。

从 $n$ 个不同元素中取出 $m$ 个组成一个集合有两类方法：取 $n$ 号元素、不取 $n$ 号元素。若取 $n$ 号元素，则应在剩余 $n - 1$ 个元素中选出 $m - 1$ 个，有 $C_{n - 1}^{m - 1}$ 种取法。若不取 $n$ 号元素，则应在剩余 $n - 1$ 个元素中选出 $m$ 个，有 $C_{n - 1}^{m}$ 种取法。根据加法原理，性质2成立。

从 $n$ 个不同元素中取出若干个元素组成一个集合，有 $n + 1$ 类方法，分别是取出 $0,1,2,\dots ,n$ 个。根据加法原理，共有 $C_n^0 +C_n^1 +C_n^2 +\dots +C_n^n$ 种方法。从另一个方面去想， $n$ 个元素每个元素可以取或不取，总方法数显然为 $2^{n}$ ，二者相等，故性质3成立。

证毕。

组合数的求法

根据性质2，用递推法可求出 $0 \leq y \leq x \leq n$ 的所有组合数 $C_x^y$ ，复杂度为 $O(n^2)$ 。

组合数的结果一般较大, 若题目要求对一个数 $p$ 取模, 并且 $1 \sim n$ 都存在模 $p$ 乘法逆元, 则可以先计算分子 $n!$ , 再计算分母 $m!(n - m)!$ 每项的逆元, 全部乘起来得到 $C_n^m$ , 复杂度为 $O(n \log n)$ 。

若题目要求我们进行高精度运算，为避免除法，可用0x31节中“阶乘分解”的做法，把分子、分母快速分解质因数，把整个分子、分母对应质因子的指数相减（把分母消去），最后把剩余的质因子乘起来，复杂度为 $O(n \log n)$ 。

二项式定理

(a + b) ^ {n} = \sum_ {k = 0} ^ {n} C _ {n} ^ {k} a ^ {k} b ^ {n - k}

证明：

数学归纳法。当 $n = 1$ 时， $(a + b)^{1} = C_{n}^{0}a^{0}b^{1} + C_{n}^{1}a^{1}b^{0} = a + b$ 成立。

假设当 $n = m$ 时命题成立，当 $n = m + 1$ 时：

\begin{array}{l} (a + b) ^ {m + 1} = (a + b) (a + b) ^ {m} = (a + b) \sum_ {k = 0} ^ {m} C _ {m} ^ {k} a ^ {k} b ^ {m - k} \\ = \sum_ {k = 0} ^ {m} C _ {m} ^ {k} a ^ {k + 1} b ^ {m - k} + \sum_ {k = 0} ^ {m} C _ {m} ^ {k} a ^ {k} b ^ {m - k + 1} \\ = \sum_ {k = 1} ^ {m + 1} C _ {m} ^ {k - 1} a ^ {k} b ^ {m - k + 1} + \sum_ {k = 0} ^ {m} C _ {m} ^ {k} a ^ {k} b ^ {m - k + 1} \\ = \sum_ {k = 0} ^ {m + 1} \left(C _ {m} ^ {k - 1} + C _ {m} ^ {k}\right) a ^ {k} b ^ {m - k + 1} = \sum_ {k = 0} ^ {m + 1} C _ {m + 1} ^ {k} a ^ {k} b ^ {m + 1 - k} \\ \end{array}

证毕。

【例题】计算系数 NOIP2011/CODEVS1137

给定一个多项式 $(ax + by)^k$ ，求出多项式展开后 $x^n y^m$ 项的系数，对10007取模。 $0 \leq n, m \leq k \leq 1000, n + m = k, 0 \leq a, b \leq 10^6$ 。

根据二项式定理，有 $(ax + by)^k = \sum_{i=0}^k C_k^i a^i b^{k-i} x^i y^{k-i}$ ，所以 $x^n y^m$ 项的系数即为 $C_k^n a^n b^m$ ，直接计算 $a^n b^m$ 和组合数即可。因为10007是质数，所以 $1 \sim 1000$ 的整数都存在模10007的乘法逆元，组合数中的除法可用逆元转化为乘法计算。

多重集的排列数

多重集是指包含重复元素的广义集合。设 $S = \{n_{1} \cdot a_{1}, n_{2} \cdot a_{2}, \dots, n_{k} \cdot a_{k}\}$ 是由 $n_{1}$ 个 $a_{1}$ ， $n_{2}$ 个 $a_{2} \dots n_{k}$ 个 $a_{k}$ 组成的多重集。 $S$ 的全排列个数为：

\frac {n !}{n _ {1} ! n _ {2} ! \cdots n _ {k} !}

多重集的组合数

设 $S = \{n_{1} \cdot a_{1}, n_{2} \cdot a_{2}, \dots, n_{k} \cdot a_{k}\}$ 是由 $n_{1}$ 个 $a_{1}$ , $n_{2}$ 个 $a_{2}$ , $\dots$ , $n_{k}$ 个 $a_{k}$ 组成的多重集，设整数 $r \leq n_{i} (\forall i \in [1, k])$ 。从 $S$ 中取出 $r$ 个元素组成一个多重集（不考虑顺序），产生的不同多重集的数量为：

C _ {k + r - 1} ^ {k - 1}

证明：

原问题等价于统计下列集合的数量： $\{x_{1}\cdot a_{1},x_{2}\cdot a_{2},\dots ,x_{k}\cdot a_{k}\}$ ，其中 $\sum_{i = 1}^{k}x_{i} = r$ 并且 $x_{i}\leq n_{i}$ 。因为 $r\leq n_i$ ，必定有 $x_{i}\leq n_{i}$ ，所以只需考虑 $\sum_{i = 1}^{k}x_{i} = r$ 这一个条件。故原问题等价于 $r$ 个0， $k - 1$ 个1构成的全排列数—— $k - 1$ 个1把 $r$ 个0分成 $k$ 组，每组的0的数量对应 $x_{i}$ 。而多重集 $\{r\cdot 0,(k - 1)\cdot 1\}$ 的全排列数为：

\frac {(r + k - 1) !}{r ! (k - 1) !} = C _ {k + r - 1} ^ {r} = C _ {k + r - 1} ^ {k - 1}

对于更为一般的 $r$ 的情况，我们将在下一节继续讨论。

证毕。

【例题】Counting Swaps IPSC2016C

给定一个 $1 \sim n$ 的排列 $p_1, p_2, \dots, p_n$ , 可进行若干次操作, 每次选择两个整数 $x, y$ , 交换 $p_x, p_y$ 。设把 $p_1, p_2, \dots, p_n$ 变成单调递增的排列 $1, 2, \dots, n$ 至少需要 $m$ 次交换。求有多少种操作方法可以只用 $m$ 次交换达到上述目标。因为结果可能很大, 你只需要输出对 $10^9 + 9$ 取模之后的值。 $1 \leq n \leq 10^5$ 。

例如排列2,3,1至少需要2次交换才能变为1,2,3。操作方法共有3种，分别是：

先交换数字2,3，变成3,2,1，再交换数字3,1，变成1,2,3。
先交换数字 2,1，变成 1,3,2，再交换数字 3,2，变成 1,2,3。
先交换数字 3,1，变成 2,1,3，再交换数字 2,1，变成 1,2,3。

对于一个排列 $p_1, p_2, \dots, p_n$ ，如果从每个 $i$ 向 $p_i$ 连一条边，那么可以得到一张 $n$ 个点 $n$ 条边的图，并且这张图由若干个环构成。

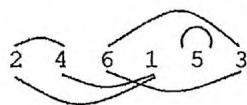
例如排列2,4,6,1,5,3对应下图，有1-2-4，3-6和5三个环。

最后的目标排列为 $1,2,\dots ,n$ ，显然由 $\pmb{n}$ 个自环构成。

引理：

把一个长度为 $n$ 的环变成 $n$ 个自环，最少需要 $n - 1$ 次交换操作。

证明：

首先，把长度为2的环变为2个自环，显然需要1次交换操作。

假设 $\forall k \leq n - 1$ , 把长度不超过 $k$ 的环变成 $k$ 个自环最少需要 $k - 1$ 次交换操作。当 $k = n$ 时, 设该环为 $v_{1} \rightarrow v_{2} \rightarrow v_{3} \rightarrow \dots \rightarrow v_{n} \rightarrow v_{1}$ , 交换任意 $v_{i}, v_{j} (i < j)$ 的出边后, 该环被拆成 $v_{i + 1} \rightarrow v_{i + 2} \rightarrow \dots \rightarrow v_{j} \rightarrow v_{i + 1}$ 和 $v_{1} \rightarrow v_{2} \rightarrow \dots \rightarrow v_{i} \rightarrow v_{j + 1} \rightarrow v_{j + 2} \rightarrow \dots \rightarrow v_{n} \rightarrow v_{1}$ 两个环, 二者的长度分别是 $j - i$ 和 $n - (j - i)$ 。把二者分别拆成自环, 所需的最小交换次数为 $(j - i - 1) + (n - (j - i) - 1) = n - 2$ , 再加上刚才 $v_{i}, v_{j}$ 的一次交换, 共需 $n - 1$ 次交换操作。最后由数学归纳法可知, 原命题成立。

证毕。

设 $F_{n}$ 表示用最少的步数把一个长度为 $n$ 的环变成 $n$ 个自环，共有多少种操作方法。由上面的证明过程可知，把一个长度为 $n$ 的环变成 $n$ 个自环的过程中，可以把该环拆成长度为 $x$ 和 $y$ 的两个环，其中 $x + y = n$ 。设 $T(x, y)$ 表示有多少种交换

方法可以把长度为 $n$ 的环变成长度为 $x$ 和 $y$ 的两个环，容易发现：

T (x, y) = \left\{ \begin{array}{l l} n / 2 & \quad n \text {是 偶 数 并 且} x = y \\ n & \quad n \text {是 奇 数 或} x \neq y \end{array} \right.

另外，二者各自变为自环的方法数为 $F_{x}$ 和 $F_{y}$ ，步数为 $x - 1$ 和 $y - 1$ 。

根据多重集的排列数、加法原理和乘法原理：

F _ {n} = \sum_ {x + y = n} T (x, y) * F _ {x} * F _ {y} * \frac {(n - 2) !}{(x - 1) ! (y - 1) !}

如果最初的排列 $p_1, p_2, \dots, p_n$ 由长度为 $l_1, l_2, \dots, l_k$ 的 $k$ 个环构成，其中 $l_1 + l_2 + \dots + l_k = n$ ，那么最终的答案就是：

F _ {l _ {1}} * F _ {l _ {2}} * \dots * F _ {l _ {k}} * \frac {(n - k) !}{(l _ {1} - 1) ! * (l _ {2} - 1) ! * \dots * (l _ {k} - 1) !}

$10^{9} + 9$ 是一个质数，可以用乘法逆元处理上面公式中的除法。整个算法的时间复杂度为 $O(n^{2})$ 。事实上，我们递推求出 $F_{n}$ 的前几项找规律，或者把前几项输入到 OEIS 网站中，可发现通项公式 $F_{n} = n^{n - 2}$ ，从而进一步优化到 $O(n \log n)$ 。

Lucas定理

若 $p$ 是质数，则对于任意整数 $1 \leq m \leq n$ ，有：

C _ {n} ^ {m} \equiv C _ {n \bmod p} ^ {m \bmod p} * C _ {n / p} ^ {m / p} (\bmod p)

也就是把 $n$ 和 $m$ 表示成 $p$ 进制数，对 $p$ 进制下的每一位分别计算组合数，最后再乘起来。证明一般需要用到生成函数知识，此处省略，感兴趣的读者可查阅相关资料。

【例题】古代猪文 BZOJ1951

给定整数 $q, n$ $(1 \leq q, n \leq 10^{9})$ , 计算 $q^{\sum d|n} C_{n}^{d} \mod 999911659$ 。

若 $q = 999911659$ ，则上式结果为0。否则，因为999911659是质数，所以 $q, n$ 互质。由欧拉定理的推论得：

q ^ {\sum_ {d \mid n} C _ {n} ^ {d}} \equiv q ^ {\sum_ {d \mid n} C _ {n} ^ {d} \mod 9 9 9 9 1 1 6 5 8} (\mathrm {m o d} 9 9 9 9 1 1 6 5 9)

因此，本题的关键是计算 $\sum_{d|n} C_n^d \mod 999911658$ 。

尝试分解质因数，可以发现 $999911658 = 2 \times 3 \times 4679 \times 35617$ 。我们称这样的

数为 square-free-number, 它的所有质因子的指数都是 1。

我们可以枚举 $n$ 的约数 $d$ ，然后运用Lucas定理求组合数 $C_n^d$ ，分别计算出 $\sum_{d \mid n} C_n^d$ 对2,3,4679,35617四个质数取模的结果，记为 $a_1, a_2, a_3, a_4$ 。在计算过程中，对于一个质数 $p$ ，预处理 $p$ 以内的所有阶乘以及阶乘的模 $p$ 乘法逆元，就能快速计算按照 $p$ 进制表示之后，每一位对应的组合数。

最后，用中国剩余定理求解线性同余方程组：

\left\{ \begin{array}{l} x \bmod 2 = a _ {1} \\ x \bmod 3 = a _ {2} \\ x \bmod 4 7 6 9 = a _ {3} \\ x \bmod 3 5 6 1 7 = a _ {4} \end{array} \right.

即可得到 $\sum_{d \mid n} C_n^d \mod 999911658$ 的最小非负整数解 $x$ 。再用快速幂求 $q^x$ 即可得到原问题的答案。

Catalan数列

给定 $n$ 个0和 $n$ 个1，它们按照某种顺序排成长度为 $2n$ 的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为：

C a t _ {n} = \frac {C _ {2 n} ^ {n}}{n + 1}

证明：

令 $n$ 个0和 $n$ 个1随意排成一个长度为 $2n$ 的序列 $S$ ，若 $S$ 不满足任意前缀中0的个数都不少于1的个数的序列的数量，则存在一个最小的位置 $2p + 1 \in [1,2n]$ ，使得 $S[1 \sim 2p + 1]$ 中有 $p$ 个0、 $p + 1$ 个1。而把 $S[2p + 2 \sim 2n]$ 中的所有数字取反后，包含 $n - p - 1$ 个0和 $n - p$ 个1。于是我们得到了由 $n - 1$ 个0和 $n + 1$ 个1排成的序列。

同理，令 $n - 1$ 个0和 $n + 1$ 个1随意排成一个长度为 $2n$ 的序列 $S^{\prime}$ ，也必定存在一个最小的位置 $2p^{\prime} + 1$ ，使得 $S^{\prime}[1 \sim 2p^{\prime} + 1]$ 中有 $p^{\prime}$ 个0、 $p^{\prime} + 1$ 个1。把 $S^{\prime}$ 后面剩下的一半取反，就得到了由 $n$ 个0和 $n$ 个1排成的、存在一个前缀0比1多的序列。

因此，以下两种序列构成一个双射：

由 $n$ 个0和 $n$ 个1排成的、存在一个前缀0比1多的序列。
由 $n - 1$ 个0和 $n + 1$ 个1排成的序列。

根据组合数的定义，后者显然有 $C_{2n}^{n-1}$ 个。

综上所述，由 $n - 1$ 个0和 $n + 1$ 个1排成的、任意前缀中0都不少于1的序列数量为：

C _ {2 n} ^ {n} - C _ {2 n} ^ {n - 1} = \frac {(2 n) !}{n ! n !} - \frac {(2 n) !}{(n - 1) ! (n + 1) !} = \frac {C _ {2 n} ^ {n}}{n + 1} = C a t _ {n}

证毕。

推论

以下问题都与Catalan数有关：

$n$ 个左括号和 $n$ 个右括号组成的合法括号序列的数量为 $Cat_{n}$ 。
$1,2,\dots ,n$ 经过一个栈，形成的合法出栈序列的数量为 $Cat_{n}$ 。
$n$ 个节点构成的不同二叉树的数量为 $Cat_{n}$ 。
在平面直角坐标系上，每一步只能向上或向右走，从 $(0,0)$ 走到 $(n,m)$ 并且除两个端点外不接触直线 $y = x$ 的路线数量为 $2Cat_{n-1}$ 。

0x36_组合计数