2._为什么引入特征值与特征向量

本章内容总体概述：假设有一头猪，我们要给他拍照，首先会选一个视角，这个视角就是矩阵（你也可以把这个矩阵理解为一个“参照物”），我们可以从不同视角给猪拍照，这些不同的视角和最初的视角是彼此相似的，如何找到不同的视角利用的就是特征值与特征向量。在这些视角里，会有一个比较好的视角（你可以理解为给猪正面拍照），这就是矩阵的对角化。 我们发现不是每个矩阵都可以对角化的，但是实对称矩阵一定可以对角化，所以，我们提出了正交相似（矩阵是一个二维表格，如果是对称矩阵，则他相当于对$x,y$轴进行了同比例缩放，自然图像不会坍塌）。如果这个对称矩阵的行列式的值为1或者-1，这个矩阵就是正交矩阵。使用正交矩阵产生的变换就是正交变换。当使用正交变换时，图像不变（长度、角度都不变），进一步可以简单的理解为正交变换就是坐标轴的旋转。

从上面的介绍，可以看到，在对矩阵的变换里，我们是层层推进的 （1）先找相似矩阵 （2）在找相似对角化 （3）再找对称矩阵的对角化 （4）再找行列式的值为1或者-1的对称矩阵的对角化，即正交矩阵。 而普通矩阵转为正交矩阵使用的是 施密特正交化工具。

为什么引入特征值与特征向量

引例1

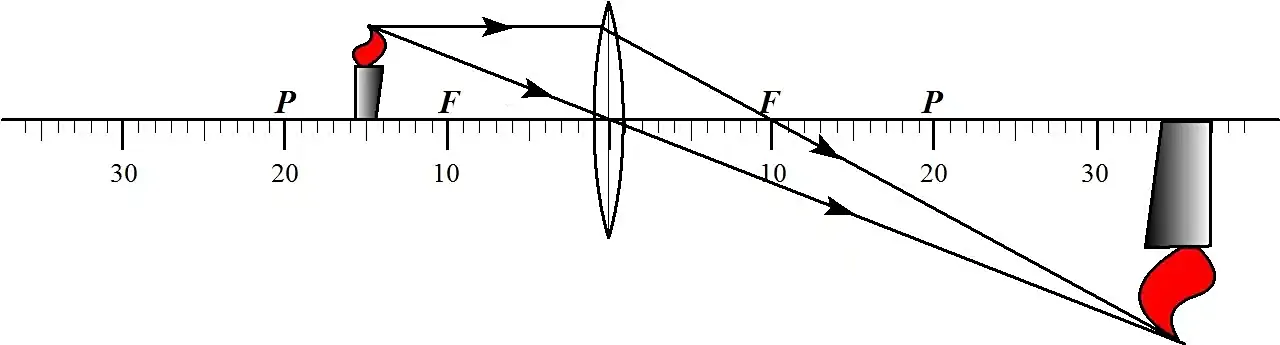
特征值与特征向量反映的是矩阵变换里的不变量（方向不变）。这句话可能不好理解，所以，先看初中学过的凸透镜成像。 在初中物理里，我们都学过凸透镜成像，凸透镜成像核心口诀有2句： （1）平行于主轴的光线经过成像后经过焦点 （2）经过凸透镜中心的光线方向不变 这2个直线相交，就获得了“像”的位置，所以，物体成像虽然复杂，但是抓住核心的几个不变点，就能找到像的规律 {width=600px}

引例2

矩阵作用向量，会使得向量发生缩放与旋转，但是总有一些向量只伸缩不旋转。因为线性的关系，通常我们只需要抓住几个关键点，就能描述变换的规律。比如 剪切矩阵 K

$K$作用在 $OAG$上， 如果我们能找到 $A',G'$ 这两个关键点，那么 自然的 $O A ' G'$ 就是 $OAG$ 变换后的像,如下图所示

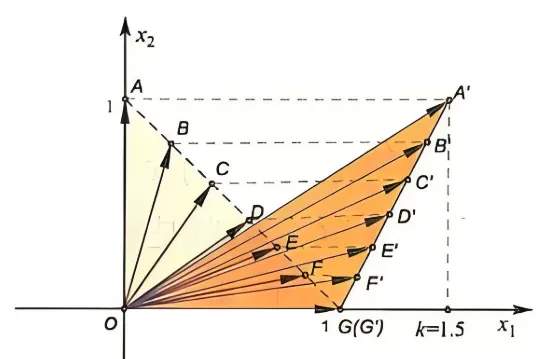
直角三角形 $\triangle O A G$ 内部的无数向量被水平方向切变到 $\triangle O A^{\prime} G^{\prime}$ 钝角三角形内部的向量。图中，原向量与被变换的向量由一根根虚线段 $\left(A A^{\prime}, B B^{\prime}, \cdots, G G^{\prime}\right)$ 连接，因为是水平切变，因此这根虚线段所代表的向量差是水平的。

显然，这些虚线段 $A A^{\prime}, B B^{\prime}, \cdots, G G^{\prime}$ 所表示的向量变化量是由矩阵 $\left[\begin{array}{cc}1 & 1.5 \\ 0 & 1\end{array}\right]$ 带来的；这些变换量的特点是 $A A^{\prime}$ 线段最长，$B B^{\prime}$ 线段长度次之，$\cdots \cdots$ 直到 $G G^{\prime}$ 线段长度变为 0 。这时原向量 $\overrightarrow{O G}$ （ $x$ 坐标单位向量）和变换向量 $\overrightarrow{o G^{\prime}}$ 重合。由特征值和特征向量的定义可知，向量 $\overrightarrow{o G}=(1,0)$是矩阵 $\left[\begin{array}{cc}1 & 1.5 \\ 0 & 1\end{array}\right]$ 的特征向量，因为这个特征向量的变化量为 0 ，原向量与被变换向量相等，变换的比例为 1 ，所以特征值是 1 。

进一步的，复杂图像是由简单几何体构成而成，而几何体由一根根向量组成,这样，对微观向量的改变就会导致宏观图像的改变。下图展示了矩阵作用图片后的水平拉伸效果。

{width=500px}

因此，矩阵的特征值和特征向量相当于帮助我们找到矩阵变换里的不变量。

特征值和特征向量的作用

为了方便理解为什么要引入特征值与特性向量，我们先看一个结论：如果有了特征值与特征向量他们有什么作用。 一个简单的作用是可以找到一个新基，在新基下可以实现对图形进行“扶正”。

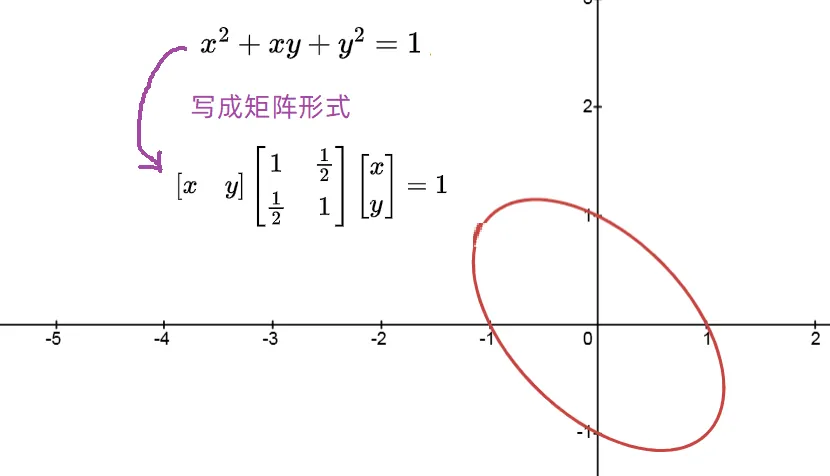
假设给你一个斜椭圆方程 $x^2+xy+y^2=1$ ,画出其图像如下，如果问椭圆长轴长和短轴长是多少，其实并不容易求出，因为他们不是我们遇到的标准椭圆（椭圆的标准方程是 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$），但是利用特征值与特征向量就可以把图像扶正。

{width=500px}

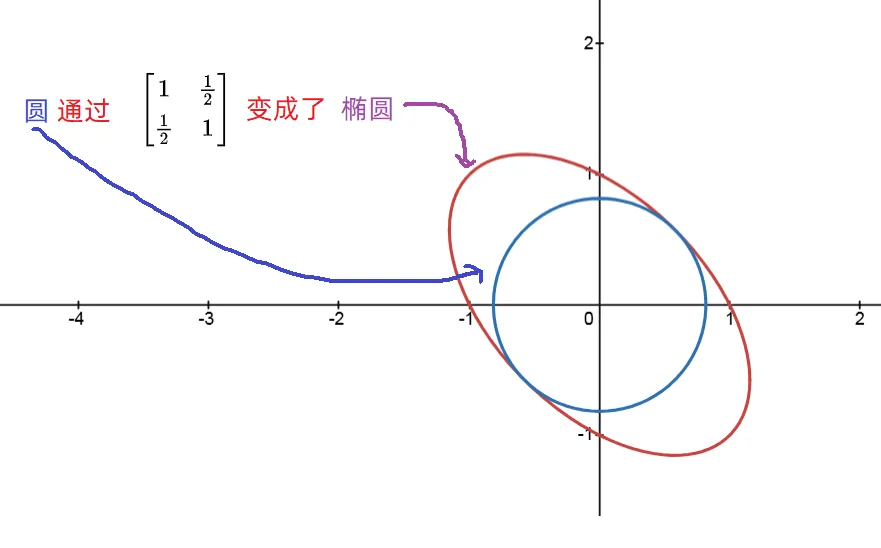
“扶正”的过程可能比较难理解，这时候我们反向思考，如果最开始是一个圆，它通过某个线性变换，拉伸并旋转成了上面的椭圆，我们现在要做的就是看看圆是怎么变成椭圆的。 在这里，要插入一个小知识（关于二次型）：因为笛卡尔直角坐标系是最基础的坐标系，所以，所有图形都是以该坐标系为基础，而

表示的正好是单位圆 (即$x^2+y^2=1$)，所以上面的问题可以描述为圆是怎么通过下面的矩阵A变为斜椭圆的。

提示：事实上，圆不应该把他当做由点组成，而应该把圆当做由一个个向量组成。这里直接说由点组成，只是为了方便理解。

{width=500px}

矩阵分解

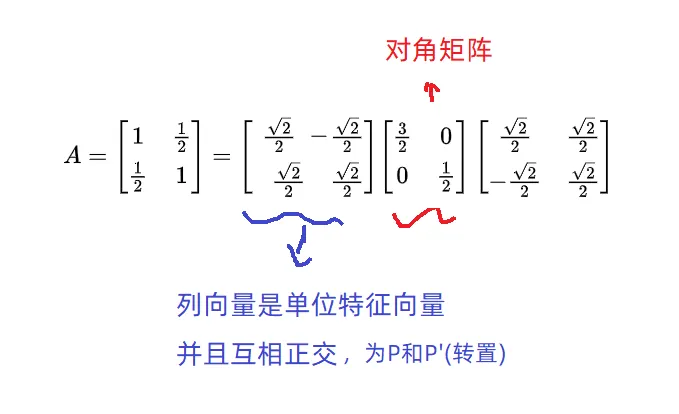
矩阵分解和因式分解类似，比如$25 * 12 =25 * 4 * 3$,把$12$分解为$4 * 3$,然后利用$25 * 4=100$ 就很容易计算。 矩阵作用于向量，相当于对向量进行了“缩放”和“旋转”，而特征值相当于缩放倍数，特征向量相当于找到了一组正交基。 现在把上面的矩阵A进行分解的，参考下图 （矩阵A分解成了3个矩阵相乘，可能你会疑惑这3个矩阵相乘真的等于$A$吗？你可以自己验算一下，确实等于$A$，即$A=P \Lambda P^{-1}$）

{width=500px}

对角矩阵的对角线上是特征值，一个矩阵表示的线性变换，只有特征值才有拉伸作用，拉伸方向就是对应的特征向量方向，显然特征值越大拉伸得越长，其它方向上的拉伸都是“被动拉伸”，所以椭圆的长轴就是最大特征值的拉伸结果。

两边的矩阵是旋转矩阵，这里进行了单位化，稍后进行解释，

至此，我们大致能了解“圆”是怎么变成“斜椭圆”的，首先坐标轴先逆时针旋转$45^{\circ}$,接着把圆想象为弹性皮筋，手捏住两端拉伸，往上拉伸了$\frac{3}{2}$， 往左右拉伸了$\frac{1}{2}$ , 即可得到斜椭圆。

注意：

是线性变换里常使用的一个旋转$45^{\circ}$ 矩阵， 关于旋转矩阵见旋转矩阵

当然后面又乘以了$P^{-1}$，他是顺时针旋转$45^{\circ}$，相当于再把坐标系再还原回来。

特征值与特征向量的作用

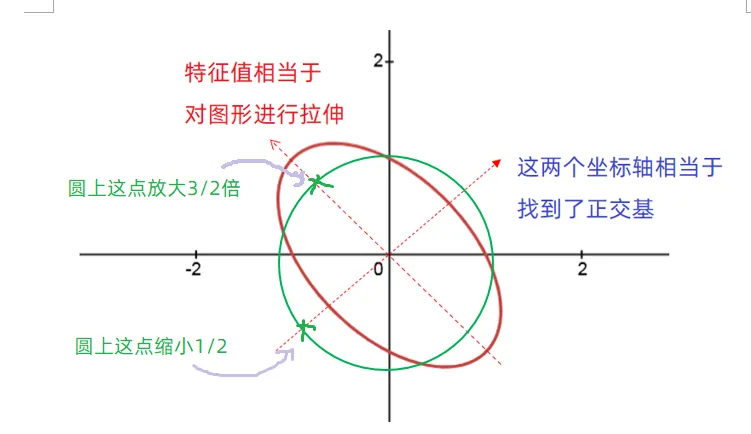
通过上面的操作，可以看到特征向量相当于帮助我们找到了一个正交基，而特征值相当于在找到的正交基里，各个维度缩放的倍数，参考下图红色的虚坐标轴。

{width=500px}

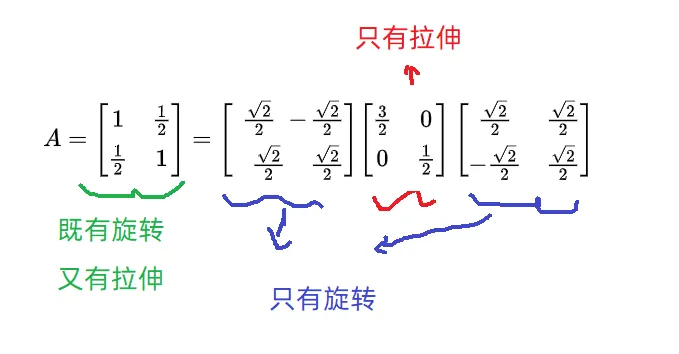
最终，矩阵作用在一个向量上的两个操作（缩放与旋转）被分解为了缩放和旋转，如下图 （$A=P \Lambda P^{-1}$, 前面左乘P相当于找到的新基，中间是拉伸，沿着新基的各个方向进行缩放，右边右乘$P^{-1}$表示变换完了新基再转回来）

{width=500px}

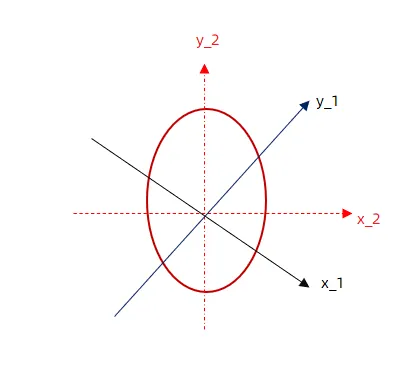
从上面介绍可以看到，在红色新坐标系下斜椭圆变成了标准椭圆（$(x_1,y_1)$为旧坐标系$(x_2,y_2)$为新坐标系）

为什么要单位化

如果你计算上面A的特征向量将是

但是单位化后变为

这是因为：坐标基单位化后，图形长度不变（在本例中计算长、短半轴长），如果使用$E_1$作为坐标基，将影响尺寸。

那么，何时需要单位化呢？具体看需求，比如，如果你想测量两个直线的角度，直接矩阵相似即可，不需要单位化，如果需要测量两个线段的距离，就需要单位化。 理解这个思想可以类比全等三角形和相似三角形，如果求角度相似三角形就可以了，如果求长度，就必须使用全等三角形。

通过例题解释特征值域特征向量

特征值与特征向量相当于给我们找到了一个“新坐标系”，特征向量表示图形变换里，方向不变的量，特征值相当于缩放的比例，下面的例题进一步解释了这句话的意思。

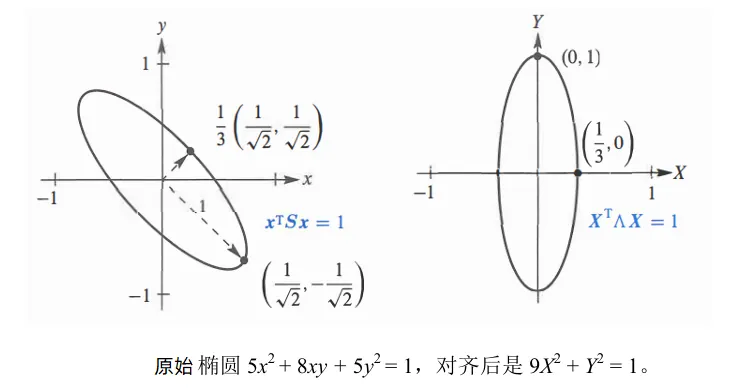
例 求出椭圆 $5 x^2+8 x y+5 y^2=1$ 的轴 解析：如果画出他的几何图形，可以看到他是一个斜椭圆，参考下图（左图）。

注意：这里涉及到后面的二次型，我们很容易利用二次型写出他的方程为 $\left[\begin{array}{ll}x & y\end{array}\right]\left[\begin{array}{ll}5 & 4 \\ 4 & 5\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]=1 \quad$

得变换矩阵 $\quad S=\left[\begin{array}{ll}5 & 4 \\ 4 & 5\end{array}\right]$

如果求矩阵的特征值和特征向量，可以得到 ① 当特征值 $\lambda=1$ 时，特征向量$X_1= \begin{bmatrix} -1 \\ 1 \end{bmatrix}$

① 当特征值 $\lambda=9$ 时，特征向量$X_2= \begin{bmatrix} 1 \\ 1 \end{bmatrix}$

这意味着，如果我们使用特征向量 $X_1 o X_2$ 建立新坐标系，那么“椭圆”将进行扶正，即变成了标准椭圆，参考下图（右图）。 整个变换可以理解为有三部： 1．原始的椭圆对应 $S$ ，它的方程式$5 x^2+8 x y+5 y^2=1$ 对应的矩阵乘法是 $x ^{ T } S x =1$ 。 2．修正后的椭圆对应 $\Lambda$ ，它的方程式$9X^2+Y^2=1$ 对应的矩阵乘法 $X^{ T } \Lambda X=1$ 3．使得原始椭圆旋转对齐的旋转矩阵是特征向量矩阵 $Q$ ，这个$Q$ 就是后面介绍的 正交矩阵。

注意：对于特征值和特征向量的理解，本文一开始介绍主要是方便了解本质，但是如果每个变换如果都这么想累也累死的，一个通俗的理解是：特征向量找到了一个新的坐标系，把旧坐标系旋转到新坐标系，同时在新坐标系里沿特征值缩放倍数，这么理解就可以了。我们也不用太在意到底是$x$轴还是$y$轴，因为我们研究的都是对称矩阵，对对称矩阵来说，作用在$x,y$上也是对称的。另外，坐标不变图形变换 和 图形不变坐标变换 有时候说不清。 就像是地球绕着太阳转还是太阳绕着地球转，对分析结果影响不大。

例下面再看一个例题，有一个矩阵

我们计算得到他的特征值和特征向量。并用他的特征向量组成一个新的坐标系，具体求解见矩阵相似

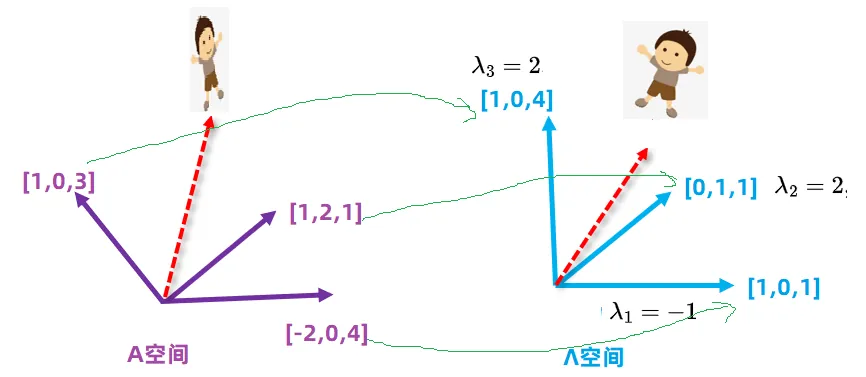
可以求的特征值 $\lambda_1=-1, \lambda_2=\lambda_3=2$ 和 特征向量 $p_1,p_2,p_3$ , 具体求解请参考 此处

想象一下你在$A$空间看到的一个小男孩，经过特征转换后，找到了一个新的空间，我们称他为特征空间，在这个特征空间里，你看到的小男孩更简洁、更漂亮。

注意：在上面这个变换后的特征空间里，他的坐标系其实并不一定互相垂直，这里会有一个重要结论：普通矩阵$A$的特征空间不一定互相垂直（数学上证明很难），但是如果$A$是对称矩阵，那么他的特征空间一定互相垂直，所以后面我们主要研究对称矩阵。

本节旨在介绍特征值与特征向量的常见用法，下一节将更深一步探讨特征值和特征向量的意义。