特征值与特征向量的求法 在上面介绍的特征值与特征向量的意义,主要是方便读者理解,线性代数的奇妙之处就在于,你哪怕完全不理解其意义,按照固定的套路,也能作对题目,考试时不会考察你理解不理解他的意义,考试主要还是做题。
一个任意给定的 n n n A A A A A A λ \lambda λ λ \lambda λ α \alpha α A α = λ α A \alpha=\lambda \alpha A α = λ α A α = λ α A \alpha=\lambda \alpha A α = λ α
( A − λ E ) α = 0 , (A-\lambda E) \alpha=\mathbf{0}, ( A − λ E ) α = 0 , 可见, α \alpha α n n n n n n ( A − λ E ) x = 0 (A-\lambda \boldsymbol{E}) \boldsymbol{x}=\mathbf{0} ( A − λ E ) x = 0
∣ A − λ E ∣ = 0 |A-\lambda \boldsymbol{E}|=0 ∣ A − λ E ∣ = 0 记
f ( λ ) = ∣ A − λ E ∣ = ∣ a 11 − λ a 12 ⋯ a 1 n a 21 a 22 − λ ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a 11 a 12 ⋯ a n n − λ ∣ , f(\lambda)=|\boldsymbol{A}-\lambda \boldsymbol{E}|=\left|\begin{array}{cccc}
a_{11}-\lambda & a_{12} & \cdots & a_{1 n} \\
a_{21} & a_{22}-\lambda & \cdots & a_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{11} & a_{12} & \cdots & a_{n n}-\lambda
\end{array}\right|, f ( λ ) = ∣ A − λ E ∣ = a 11 − λ a 21 ⋮ a 11 a 12 a 22 − λ ⋮ a 12 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a nn − λ , 则 f ( λ ) f(\lambda) f ( λ ) λ \lambda λ A A A 特征多项式 . 从而公式 ∣ A − λ E ∣ = 0 |A-\lambda E|=0 ∣ A − λ E ∣ = 0 f ( λ ) = 0 f(\lambda)=0 f ( λ ) = 0 λ \lambda λ n n n A \boldsymbol{A} A 特征方程 ,而 A \boldsymbol{A} A
我们知道,一元 n n n n n n n n n A A A n n n A A A n n n λ = λ i \lambda=\lambda_i λ = λ i A \boldsymbol{A} A ( A − λ i E ) x = 0 \left(\boldsymbol{A}-\lambda_i \boldsymbol{E}\right) \boldsymbol{x}=\mathbf{0} ( A − λ i E ) x = 0 x = α i ′ \boldsymbol{x}=\boldsymbol{\alpha}_{i^{\prime}} x = α i ′ α i \alpha_i α i A A A λ i \lambda_i λ i λ i \lambda_i λ i α \alpha α λ i \lambda_i λ i α i \alpha_i α i
在构造特征多项式时,使用∣ λ E − A = 0 ∣ |\lambda \boldsymbol{E}-A=0| ∣ λ E − A = 0∣ ∣ A − λ E ∣ = 0 |A-\lambda \boldsymbol{E}|=0 ∣ A − λ E ∣ = 0
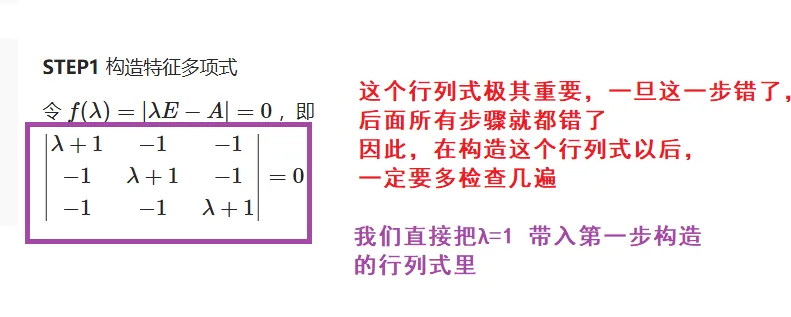
特征值与特征向量求解套路 例 求 A = [ − 1 1 1 1 − 1 1 1 1 − 1 ] A=\left[\begin{array}{ccc}-1 & 1 & 1 \\ 1 & -1 & 1 \\ 1 & 1 & -1\end{array}\right] A = − 1 1 1 1 − 1 1 1 1 − 1 STEP1 构造特征多项式
令 f ( λ ) = ∣ λ E − A ∣ = 0 f(\lambda)=|\lambda E - A |=0 f ( λ ) = ∣ λ E − A ∣ = 0
∣ λ + 1 − 1 − 1 − 1 λ + 1 − 1 − 1 − 1 λ + 1 ∣ = 0 \left|\begin{array}{ccc}
\lambda+1 & -1 & -1 \\
-1 & \lambda+1 & -1 \\
-1 & -1 & \lambda+1
\end{array}\right|=0 λ + 1 − 1 − 1 − 1 λ + 1 − 1 − 1 − 1 λ + 1 = 0 STEP2 化简三阶行列式 这是一个三阶行列式,三阶行列式是三次方程,我们并没有三次方程的通用公式,此时要尽可能因式分解,提取一个系数。
从这里也看到,第一章介绍的行列式 其实也是作为一个工具,为此处服务的。
D = r 3 + r 2 + r 1 ∣ λ − 1 λ − 1 λ − 1 − 1 λ + 1 − 1 − 1 − 1 λ + 1 ∣ = ( λ − 1 ) ∣ 1 1 1 − 1 λ + 1 − 1 − 1 − 1 λ + 1 ∣ = ( λ − 1 ) ∣ 1 1 1 0 λ + 2 0 0 0 λ + 2 ∣ = ( λ − 1 ) ( λ + 2 ) 2 , \begin{aligned}
& D\xlongequal{r_3+r_2+r_1}\left|\begin{array}{ccc}
\lambda-1 & \lambda-1 & \lambda-1 \\
-1 & \lambda+1 & -1 \\
-1 & -1 & \lambda+1
\end{array}\right| \\
& =(\lambda-1)\left|\begin{array}{ccc}
1 & 1 & 1 \\
-1 & \lambda+1 & -1 \\
-1 & -1 & \lambda+1
\end{array}\right| \\
& =(\lambda-1)\left|\begin{array}{ccc}
1 & 1 & 1 \\
0 & \lambda+2 & 0 \\
0 & 0 & \lambda+2
\end{array}\right| \\
& =(\lambda-1)(\lambda+2)^2,
\end{aligned} D r 3 + r 2 + r 1 λ − 1 − 1 − 1 λ − 1 λ + 1 − 1 λ − 1 − 1 λ + 1 = ( λ − 1 ) 1 − 1 − 1 1 λ + 1 − 1 1 − 1 λ + 1 = ( λ − 1 ) 1 0 0 1 λ + 2 0 1 0 λ + 2 = ( λ − 1 ) ( λ + 2 ) 2 , 得 A A A λ 1 = 1 , λ 2 = λ 3 = − 2 \lambda_1=1, \lambda_2=\lambda_3=-2 λ 1 = 1 , λ 2 = λ 3 = − 2
STEP3 求基础解系 上面得到2个特征值,要根据每个特征值找到特征向量,这个特征向量就是方程组的基础解系,这里又转换为了 齐次方程组基础解系的求法 里了。
①当 λ 1 = 1 \lambda_1=1 λ 1 = 1 ( E − A ) X = 0 ( E - A ) X = 0 ( E − A ) X = 0
我们在STEP1里,已经构造了行列式,所以直接带入λ 1 = 1 \lambda_1=1 λ 1 = 1
他其实就是下面的方程(考试时可以不写)。
( 2 − 1 − 1 − 1 2 − 1 − 1 − 1 2 ) ( x 1 x 2 x 3 ) = ( 0 0 0 ) \left(\begin{array}{rrr}
2 & -1 & -1 \\
-1 & 2 & -1 \\
-1 & -1 & 2
\end{array}\right)\left(\begin{array}{l}
x_1 \\
x_2 \\
x_3
\end{array}\right)=\left(\begin{array}{l}
0 \\
0 \\
0
\end{array}\right) 2 − 1 − 1 − 1 2 − 1 − 1 − 1 2 x 1 x 2 x 3 = 0 0 0 对系数矩阵进行初等行变换,化为行简化阶梯形,具体化简参考 阶梯形矩阵的化法 。
E − A = [ 2 − 1 − 1 − 1 2 − 1 − 1 − 1 2 ] → [ 2 − 1 − 1 0 3 2 − 3 2 0 − 3 2 3 2 ] → [ 2 − 1 − 1 0 3 2 − 3 2 0 0 0 ] → [ 1 0 − 1 0 1 − 1 0 0 0 ] E - A =\left[\begin{array}{ccc}
2 & -1 & -1 \\
-1 & 2 & -1 \\
-1 & -1 & 2
\end{array}\right] \rightarrow\left[\begin{array}{ccc}
2 & -1 & -1 \\
0 & \frac{3}{2} & -\frac{3}{2} \\
0 & -\frac{3}{2} & \frac{3}{2}
\end{array}\right] \rightarrow\left[\begin{array}{ccc}
2 & -1 & -1 \\
0 & \frac{3}{2} & -\frac{3}{2} \\
0 & 0 & 0
\end{array}\right]
\rightarrow\left[\begin{array}{ccc}
1 & 0 & -1 \\
0 & 1 & -1 \\
0 & 0 & 0
\end{array}\right] E − A = 2 − 1 − 1 − 1 2 − 1 − 1 − 1 2 → 2 0 0 − 1 2 3 − 2 3 − 1 − 2 3 2 3 → 2 0 0 − 1 2 3 0 − 1 − 2 3 0 → 1 0 0 0 1 0 − 1 − 1 0 E − A E - A E − A ( E − A ) X = 0 ( E - A ) X = 0 ( E − A ) X = 0
{ x 1 − x 3 = 0 x 2 − x 3 = 0 \left\{\begin{array}{rrr}
x_1-x_3=0 \\
x_2-x_3=0
\end{array}\right. { x 1 − x 3 = 0 x 2 − x 3 = 0 我们根据阶梯形矩阵的结果,取每行1所在元素为未知量,其余为自由未知量。
即 取x 1 , x 2 x_1,x_2 x 1 , x 2 x 3 x_3 x 3
{ x 1 = x 3 x 2 = x 3 \left\{\begin{array}{rrr}
x_1=x_3 \\
x_2=x_3
\end{array}\right. { x 1 = x 3 x 2 = x 3 令 x 3 = 1 x_3=1 x 3 = 1 ξ 1 = [ 1 1 1 ] \xi _1=\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right] ξ 1 = 1 1 1 k 1 ξ 1 ( k 1 ≠ 0 ) k_1 \xi _1\left(k_1 \neq 0\right) k 1 ξ 1 ( k 1 = 0 ) A A A
②当 λ 2 = λ 3 = − 2 \lambda_2=\lambda_3=-2 λ 2 = λ 3 = − 2 ( − 2 E − A ) X = 0 (-2 E - A ) X = 0 ( − 2 E − A ) X = 0
我们在STEP1里,已经构造了行列式,所以直接带入 λ 2 = 2 \lambda_2=2 λ 2 = 2
对其系数矩阵作初等行变换
− 2 E − A = [ − 1 − 1 − 1 − 1 − 1 − 1 − 1 − 1 − 1 ] → [ 1 1 1 0 0 0 0 0 0 ] -2 E - A =\left[\begin{array}{lll}
-1 & -1 & -1 \\
-1 & -1 & -1 \\
-1 & -1 & -1
\end{array}\right] \rightarrow\left[\begin{array}{ccc}
1 & 1 & 1 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right] − 2 E − A = − 1 − 1 − 1 − 1 − 1 − 1 − 1 − 1 − 1 → 1 0 0 1 0 0 1 0 0 取最简形矩阵的首非零元为未知量,列出方程就是
x 1 + x 2 + x 3 = 0 x_1+x_2+x_3=0 x 1 + x 2 + x 3 = 0
取x 1 x_1 x 1 x 2 , x 3 x_2,x_3 x 2 , x 3 x 1 = − x 2 − x 3 x_1=-x_2-x_3 x 1 = − x 2 − x 3
分别取 [ x 2 = 1 x 3 = 0 ] \left[\begin{array}{cc}x_2=1\\x_3=0 \\\end{array}\right] [ x 2 = 1 x 3 = 0 ] [ x 2 = 0 x 3 = 1 ] \left[\begin{array}{cc}x_2=0\\x_3=1 \\\end{array}\right] [ x 2 = 0 x 3 = 1 ]
得
ξ 2 = [ − 1 1 0 ] , ξ 3 = [ − 1 0 1 ] \xi _2=\left[\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right]
,\quad
\xi _3=\left[\begin{array}{c}
-1 \\
0 \\
1
\end{array}\right] ξ 2 = − 1 1 0 , ξ 3 = − 1 0 1 故 k 2 ξ 2 + k 3 ξ 3 k_2 \xi _2+k_3 \xi _3 k 2 ξ 2 + k 3 ξ 3 k 2 , k 3 k_2, k_3 k 2 , k 3 A A A
例题 例求矩阵
A = ( 1 0 0 0 2 0 0 0 3 ) A=\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 3
\end{array}\right) A = 1 0 0 0 2 0 0 0 3 的特征值和特征向量.
解:矩阵 A A A
∣ A − λ E ∣ = ∣ 1 − λ 0 0 0 2 − λ 0 0 0 3 − λ ∣ = ( 1 − λ ) ( 2 − λ ) ( 3 − λ ) , |\boldsymbol{A}-\lambda \boldsymbol{E}|=\left|\begin{array}{ccc}
1-\lambda & 0 & 0 \\
0 & 2-\lambda & 0 \\
0 & 0 & 3-\lambda
\end{array}\right|=(1-\lambda)(2-\lambda)(3-\lambda), ∣ A − λ E ∣ = 1 − λ 0 0 0 2 − λ 0 0 0 3 − λ = ( 1 − λ ) ( 2 − λ ) ( 3 − λ ) , 所以 A A A λ 1 = 1 , λ 2 = 2 , λ 3 = 3 \lambda_1=1, \lambda_2=2 , \lambda_3=3 λ 1 = 1 , λ 2 = 2 , λ 3 = 3
①当 λ 1 = 1 \lambda_1=1 λ 1 = 1 ( A − E ) x = 0 (\boldsymbol{A}-\boldsymbol{E}) \boldsymbol{x}=\mathbf{0} ( A − E ) x = 0 齐次方程组解系求法 :
由
A − E = ( 0 0 0 0 1 0 0 0 2 ) → ( 0 1 0 0 0 1 0 0 0 ) \boldsymbol{A}-\boldsymbol{E}=\left(\begin{array}{lll}
0 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 2
\end{array}\right) \to \left(\begin{array}{lll}
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{array}\right) A − E = 0 0 0 0 1 0 0 0 2 → 0 0 0 1 0 0 0 1 0 得基础解系
α 1 = ( 1 0 0 ) \alpha_1=\left(\begin{array}{l}
1 \\
0 \\
0
\end{array}\right) α 1 = 1 0 0 ②当 λ 2 = 2 \lambda_2=2 λ 2 = 2 ( A − 2 E ) x = 0 (\boldsymbol{A}-2 \boldsymbol{E}) \boldsymbol{x}=\mathbf{0} ( A − 2 E ) x = 0 A − 2 E = ( − 1 0 0 0 0 0 0 0 1 ) → ( 1 0 0 0 0 1 0 0 0 ) \boldsymbol{A}-2 \boldsymbol{E}=\left(\begin{array}{ccc}-1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1\end{array}\right) \to \left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array}\right) A − 2 E = − 1 0 0 0 0 0 0 0 1 → 1 0 0 0 0 0 0 1 0 α 2 = ( 0 1 0 ) \quad \boldsymbol{\alpha}_2=\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right) α 2 = 0 1 0
③当 λ 3 = 3 \lambda_3=3 λ 3 = 3 ( A − 3 E ) x = 0 (\boldsymbol{A}-3 \boldsymbol{E}) \boldsymbol{x}=\mathbf{0} ( A − 3 E ) x = 0
A − 3 E = ( − 2 0 0 0 − 1 0 0 0 0 ) , ( 1 0 0 0 1 0 0 0 0 ) \boldsymbol{A}-3 \boldsymbol{E}=\left(\begin{array}{ccc}
-2 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & 0
\end{array}\right),\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right) A − 3 E = − 2 0 0 0 − 1 0 0 0 0 , 1 0 0 0 1 0 0 0 0 得基础解系 α 3 = ( 0 0 1 ) \quad \alpha_3=\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right) α 3 = 0 0 1
于是 k α 1 ( k ≠ 0 ) k \boldsymbol{\alpha}_1(k \neq 0) k α 1 ( k = 0 ) λ 1 = 1 \lambda_1=1 λ 1 = 1 k α 2 ( k ≠ 0 ) k \boldsymbol{\alpha}_2(k \neq 0) k α 2 ( k = 0 ) λ 2 = 2 \lambda_2=2 λ 2 = 2 k α 3 ( k ≠ 0 ) k \boldsymbol{\alpha}_3(k \neq 0) k α 3 ( k = 0 ) λ 3 = 3 \lambda_3=3 λ 3 = 3
由此例可知,对角矩阵的全部特征值就是它的对角线上的元素. 这个结论需要记住
例 求下列二阶方阵的特征值和特征向量.
(1) A = ( a 0 0 b ) , a ≠ b \boldsymbol{A}=\left(\begin{array}{ll}a & 0 \\ 0 & b\end{array}\right), a \neq b A = ( a 0 0 b ) , a = b A = ( a b b a ) , b ≠ 0 A=\left(\begin{array}{ll}a & b \\ b & a\end{array}\right), b \neq 0 A = ( a b b a ) , b = 0
∣ λ E − A ∣ = ∣ λ − a 0 0 λ − b ∣ = ( λ − a ) ( λ − b ) = 0 , |\lambda \boldsymbol{E}-\boldsymbol{A}|=\left|\begin{array}{cc}
\lambda-a & 0 \\
0 & \lambda-b
\end{array}\right|=(\lambda-a)(\lambda-b)=0, ∣ λ E − A ∣ = λ − a 0 0 λ − b = ( λ − a ) ( λ − b ) = 0 , 所以 A \boldsymbol{A} A λ 1 = a , λ 2 = b \lambda_1=a, \lambda_2=b λ 1 = a , λ 2 = b
k 1 ( 1 0 ) , k 2 ( 0 1 ) , k 1 , k 2 ≠ 0 k_1\binom{1}{0}, k_2\binom{0}{1}, k_1, k_2 \neq 0 k 1 ( 0 1 ) , k 2 ( 1 0 ) , k 1 , k 2 = 0 (2)由
∣ λ E − A ∣ = ∣ λ − a − b − b λ − a ∣ = ( λ − a ) 2 − b 2 = 0 , |\lambda \boldsymbol{E}-\boldsymbol{A}|=\left|\begin{array}{cc}
\lambda-a & -b \\
-b & \lambda-a
\end{array}\right|=(\lambda-a)^2-b^2=0, ∣ λ E − A ∣ = λ − a − b − b λ − a = ( λ − a ) 2 − b 2 = 0 , 得 A \boldsymbol{A} A λ 1 = a + b , λ 2 = a − b \lambda_1=a+b, \lambda_2=a-b λ 1 = a + b , λ 2 = a − b λ 1 = a + b \lambda_1=a+b λ 1 = a + b
λ 1 E − A = ( a + b ) E − ( a b b a ) = ( b − b − b b ) , \lambda_1 \boldsymbol{E}-\boldsymbol{A}=(a+b) \boldsymbol{E}-\left(\begin{array}{ll}
a & b \\
b & a
\end{array}\right)=\left(\begin{array}{rr}
b & -b \\
-b & b
\end{array}\right), λ 1 E − A = ( a + b ) E − ( a b b a ) = ( b − b − b b ) , 得齐次线性方程组
( b − b − b b ) ( x 1 x 2 ) = ( 0 0 ) \left(\begin{array}{rr}
b & -b \\
-b & b
\end{array}\right)\binom{x_1}{x_2}=\binom{0}{0} ( b − b − b b ) ( x 2 x 1 ) = ( 0 0 ) 故得对应于特征值 λ 1 = a + b \lambda_1=a+b λ 1 = a + b
k ( 1 1 ) , k ≠ 0 k\binom{1}{1}, k \neq 0 k ( 1 1 ) , k = 0 对特征值 λ 2 = a − b \lambda_2=a-b λ 2 = a − b
λ 2 E − A = ( a − b ) E − ( a b b a ) = ( − b − b − b − b ) \lambda_2 \boldsymbol{E}-\boldsymbol{A}=(a-b) \boldsymbol{E}-\left(\begin{array}{ll}
a & b \\
b & a
\end{array}\right)=\left(\begin{array}{cc}
-b & -b \\
-b & -b
\end{array}\right) λ 2 E − A = ( a − b ) E − ( a b b a ) = ( − b − b − b − b ) 得齐次线性方程组
( − b − b − b − b ) ( x 1 x 2 ) = ( 0 0 ) \left(\begin{array}{cc}
-b & -b \\
-b & -b
\end{array}\right)\binom{x_1}{x_2}=\binom{0}{0} ( − b − b − b − b ) ( x 2 x 1 ) = ( 0 0 ) 因此对应于特征值 λ 2 = a − b \lambda_2=a-b λ 2 = a − b
k ( 1 − 1 ) , k ≠ 0 k\binom{1}{-1}, k \neq 0 k ( − 1 1 ) , k = 0 此例说明如下两点:
(1)对角矩阵的特征值就是对角线上的所有元素,同阶的单位矩阵的列向量可分别看作是它们所对应的一个特征向量;
(2)对行和相等的方阵,这个行和一定是它的一个特征值,而分量均为 1 的列向量必为这个特征值所对应的一个特征向量.
 {width=600px}
{width=600px}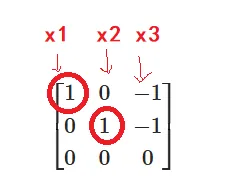
 {width=600px}
{width=600px}