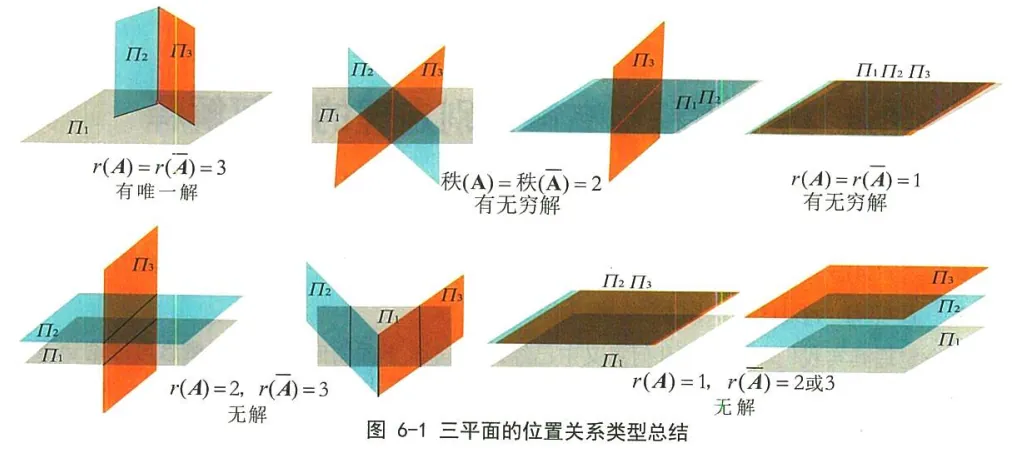
方程组解的几何意义 对于方程组:
{ a 1 x 1 + b 1 x 2 = c 1 . . . ① a 2 x 1 + b 2 x 2 = c 2 . . . ② \left\{\begin{array}{l}
a_1 x_1+b_1 x_2=c_1 ...①\\
a_2 x_1+b_2 x_2=c_2 ...②
\end{array}\right. { a 1 x 1 + b 1 x 2 = c 1 ...① a 2 x 1 + b 2 x 2 = c 2 ...② 从高中解析几何的知识我们知道上面①和②各表示一根直线, 如果用L L L
{ L 1 : x 2 = − a 1 b 1 x 1 + c 2 b 1 L 2 : x 2 = − a 2 b 2 x 1 + c 2 b 2 \left\{\begin{array}{l}
L_1: x_2=-\dfrac{a_1}{b_1} x_1 + \dfrac{c_2}{b_1} \\
L_2: x_2=-\dfrac{a_2}{b_2} x_1 + \dfrac{c_2}{b_2}
\end{array}\right. ⎩ ⎨ ⎧ L 1 : x 2 = − b 1 a 1 x 1 + b 1 c 2 L 2 : x 2 = − b 2 a 2 x 1 + b 2 c 2 因为两条直线有 相交、重合和平行三种位置关系,对应其解分别是只有一个解,有无穷多个解和无解。
方程组的解 ① 我们观察更具体的二元一次方程组,例如
{ x + y = 3 2 x + y = 5 \left\{\begin{array}{l}
x+y=3\\
2x+y=5
\end{array}\right. { x + y = 3 2 x + y = 5 分别画出他们的直线方程,如下图
可以发现,他们只有一个交点,因此方程有一个解。
{ x = 2 y = 1 \left\{\begin{array}{l}
x=2\\
y=1
\end{array}\right. { x = 2 y = 1 ② 同样的,观察下面两个方程
{ x + y = 3 2 x + 2 y = 6 \left\{\begin{array}{l}
x+y=3\\
2x+2y=6
\end{array}\right. { x + y = 3 2 x + 2 y = 6 画出他们的图形
③观察下面两个方程
{ x + y = 3 2 x + 2 y = 8 \left\{\begin{array}{l}
x+y=3\\
2x+2y=8
\end{array}\right. { x + y = 3 2 x + 2 y = 8 画出他们的图形
0 = 2 0=2 0 = 2
到这里我们可以有一个简单的结论:
有解的条件
当 r ( A ) = n r({A})=n r ( A ) = n ( α 1 , α 2 , ⋯ , α n \left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right. ( α 1 , α 2 , ⋯ , α n r ( A ) = r < n r({A})=r<n r ( A ) = r < n ( α 1 , α 2 , ⋯ , α n \left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right. ( α 1 , α 2 , ⋯ , α n n − r n-r n − r r ( A ) r(A) r ( A ) n n n
齐次线性方程与非齐次线性方程 对于线性方程组,等号右侧都为0的方程称为齐次线性方程 ,不全为0的称为非齐次线性方程 。
例如
{ x + y = 0 2 x + y = 0 \left\{\begin{array}{l}
x+y=0\\
2x+y=0
\end{array}\right. { x + y = 0 2 x + y = 0 是齐次线性方程
而
{ x + y = 3 2 x + y = 5 \left\{\begin{array}{l}
x+y=3\\
2x+y=5
\end{array}\right. { x + y = 3 2 x + y = 5 则是非齐次线性方程。
我们很容易得到,齐次线性方程一定有一个0解。但是对于齐次线性方程,我们更感兴趣的是非0解。后面我们会先研究齐次线性方程组的解系,再研究非齐次线性方程组的解系。当我们学会了齐次线性方程组的解系后,再加上常数就是非齐次线性方程组的解系(或者说,齐次线性图形经过平移后,就可以得到非齐次线性方程的图像)。
系数矩阵与增广矩阵 对于
{ x + y = 3 2 x + y = 5 \left\{\begin{array}{l}
x+y=3\\
2x+y=5
\end{array}\right. { x + y = 3 2 x + y = 5 我们把他的系数提取出来,写成矩阵,就称为系数矩阵。如
A = [ 1 1 2 1 ] A= \left[\begin{array}{ll}
1 & 1 \\
2 & 1
\end{array}\right] A = [ 1 2 1 1 ] 如果把等号右边的值也加进来,就称为增广矩阵,通常用一个竖线分割。
A ∣ b = [ 1 1 3 2 1 5 ] A|b= \left[\begin{array}{ll:l}
1 & 1 & 3\\
2 & 1 & 5
\end{array}\right] A ∣ b = [ 1 2 1 1 3 5 ] 推广到三个3元方程组的情况 对于二元一次方程组得到的解的结论,是否可以扩展到3元方程组的情况呢?答案是肯定的,如下
{ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 ( Π 1 ) a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 ( Π 2 ) a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 ( Π 3 ) \left\{\begin{array}{l}
a_{11} x_1+a_{12} x_2+a_{13} x_3=b_1\left(\Pi_1\right) \\
a_{21} x_1+a_{22} x_2+a_{23} x_3=b_2\left(\Pi_2\right) \\
a_{31} x_1+a_{32} x_2+a_{33} x_3=b_3\left(\Pi_3\right)
\end{array}\right. ⎩ ⎨ ⎧ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 ( Π 1 ) a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 ( Π 2 ) a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 ( Π 3 ) 从空间看,每个方程都表示一个平面,所以,他表示的是空间的三个平面的关系,容易知道,空间中,三个平面共有8种情况,如下图
根据线性方程组的秩及其解的不同情况, 我们可以这样总结并定义线性方程组的分类:
在这里, 要记住所有《线性代数》教材普遍使用的约定: m 、 n 、 r 、 r c m 、 n 、 r 、 r_c m 、 n 、 r 、 r c
设矩阵方程 A x = b \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} A x = b A \boldsymbol{A} A r r r m × n m \times n m × n A ‾ = [ A , b ] \overline{\boldsymbol{A}}=[\boldsymbol{A}, \boldsymbol{b}] A = [ A , b ] r c r_c r c
m m m A A A m m m n n n x i x_i x i A A A n n n r : r: r : x i x_i x i r r r r ⩽ n r \leqslant n r ⩽ n r c r_c r c r c r_c r c r ⩽ m ∘ r \leqslant m_{\circ} r ⩽ m ∘
当 r = r c = n r=r_c=n r = r c = n r = r c < n r=r_c<n r = r c < n r < r c r<r_c r < r c
下面将通过介绍3元线性方程组的解法来引入方程组解的意义,理解了三元方程,再推广到n元就不难了。
三元线性方程组的解法 如果用二元一次方程 a x + b y + c = 0 ( a , b a x+b y+c=0(a, b a x + b y + c = 0 ( a , b ) ) )
{ a 1 x + b 1 y + c 1 = 0 , a 2 x + b 2 y + c 2 = 0. . . . ( 1 ) \left\{\begin{array}{l}
a_1 x+b_1 y+c_1=0, \\
a_2 x+b_2 y+c_2=0 .
\end{array}\right. ...(1) { a 1 x + b 1 y + c 1 = 0 , a 2 x + b 2 y + c 2 = 0. ... ( 1 ) 当方程组无解时, 这两条直线平行; 当方程组有唯一解时, 两条直线相交; 当方程组有无穷多个解时, 两条直线重合.
将上述情况推广到空间, 在空间直角坐标系中, 用三元一次方程 a x + b y + c z + d = 0 a x+b y+c z+d=0 a x + b y + cz + d = 0 ( a , b , c (a, b, c ( a , b , c ) ) ) Q \mathbf{Q} Q
定义1 把含有三个未知量的一次方程组称为三元线性方程组 (system of ternary linear equations).
例如, 方程组
{ 2 x 1 + 2 x 2 + 3 x 3 = 3 , 4 x 1 + 7 x 2 + 7 x 3 = 1 \left\{\begin{array}{l}
2 x_1+2 x_2+3 x_3=3, \\
4 x_1+7 x_2+7 x_3=1
\end{array}\right. { 2 x 1 + 2 x 2 + 3 x 3 = 3 , 4 x 1 + 7 x 2 + 7 x 3 = 1 就是三元线性方程组.
例 解线性方程组
{ 2 x 1 + 2 x 2 + 3 x 3 = 3 , − 2 x 1 + 4 x 2 + 5 x 3 = − 7 , 4 x 1 + 7 x 2 + 7 x 3 = 1. \left\{\begin{aligned}
2 x_1+2 x_2+3 x_3 & =3, \\
-2 x_1+4 x_2+5 x_3 & =-7, \\
4 x_1+7 x_2+7 x_3 & =1 .
\end{aligned}\right. ⎩ ⎨ ⎧ 2 x 1 + 2 x 2 + 3 x 3 − 2 x 1 + 4 x 2 + 5 x 3 4 x 1 + 7 x 2 + 7 x 3 = 3 , = − 7 , = 1. 解: 将第一个方程加到第二个方程, 再将第一个方程乘 − 2 -2 − 2
{ 2 x 1 + 2 x 2 + 3 x 3 = 3 , 6 x 2 + 8 x 3 = − 4 , 3 x 2 + x 3 = − 5 , \left\{\begin{aligned}
2 x_1+2 x_2+3 x_3 & =3, \\
6 x_2+8 x_3 & =-4, \\
3 x_2+x_3 & =-5,
\end{aligned}\right. ⎩ ⎨ ⎧ 2 x 1 + 2 x 2 + 3 x 3 6 x 2 + 8 x 3 3 x 2 + x 3 = 3 , = − 4 , = − 5 , 在上式中交换第二个方程和第三个方程, 然后把新的第二个方程乘 − 2 -2 − 2
{ 2 x 1 + 2 x 2 + 3 x 3 = 3 , 3 x 2 + x 3 = − 5 , 6 x 3 = 6 , . . . ( 2 ) \left\{\begin{aligned}
2 x_1+2 x_2+3 x_3 & =3, \\
3 x_2+x_3 & =-5, \\
6 x_3 & =6,
\end{aligned}\right. ... (2) ⎩ ⎨ ⎧ 2 x 1 + 2 x 2 + 3 x 3 3 x 2 + x 3 6 x 3 = 3 , = − 5 , = 6 , ... ( 2 ) 由此可得 x 3 = 1 x_3=1 x 3 = 1 x 3 = 1 x_3=1 x 3 = 1 x 2 = − 2 , x 1 = 2 x_2=-2, x_1=2 x 2 = − 2 , x 1 = 2
{ x 1 = 2 , x 2 = − 2 , x 3 = 1 \left\{\begin{array}{l}
x_1=2, \\
x_2=-2, \\
x_3=1
\end{array}\right. ⎩ ⎨ ⎧ x 1 = 2 , x 2 = − 2 , x 3 = 1 分析上述例子, 在解方程组的过程中进行了三种变换:
(1)互换变换,即交换两个方程的位置;
(2)倍法变换,即用一个非零常数乘某个方程;
(3)消法变换, 即用一个常数乘某一个方程加到另一个方程上.
这些变换统称为线性方程组的初等变换 ,是高斯消元法的精髓.
系数矩阵、增广矩阵和解向量 定理1 初等变换保持线性方程组同解.
证明 只需要证明进行一次初等变换保持方程组同解. 变换(1)(2)的证明是容易的. 下面证明变换(3)不改变方程组的解.
设线性方程组
{ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 , a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 \left\{\begin{array}{l}
a_{11} x_1+a_{12} x_2+a_{13} x_3=b_1, \\
a_{21} x_1+a_{22} x_2+a_{23} x_3=b_2
\end{array}\right. { a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 , a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 的任意一个解是 x 1 = c 1 , x 2 = c 2 , x 3 = c 3 x_1=c_1, x_2=c_2, x_3=c_3 x 1 = c 1 , x 2 = c 2 , x 3 = c 3
{ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 , ( λ a 11 + a 21 ) x 1 + ( λ a 12 + a 22 ) x 2 + ( λ a 13 + a 23 ) x 3 = λ b 1 + b 2 . . . . ( 4 ) \left\{\begin{array}{l}
a_{11} x_1+a_{12} x_2+a_{13} x_3=b_1, \\
\left(\lambda a_{11}+a_{21}\right) x_1+\left(\lambda a_{12}+a_{22}\right) x_2+\left(\lambda a_{13}+a_{23}\right) x_3=\lambda b_1+b_2 .
\end{array}\right. ...(4) { a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 , ( λ a 11 + a 21 ) x 1 + ( λ a 12 + a 22 ) x 2 + ( λ a 13 + a 23 ) x 3 = λ b 1 + b 2 . ... ( 4 ) 将 x 1 = c 1 , x 2 = c 2 , x 3 = c 3 x_1=c_1, x_2=c_2, x_3=c_3 x 1 = c 1 , x 2 = c 2 , x 3 = c 3 ( λ a 11 + a 21 ) x 1 + ( λ a 12 + a 22 ) x 2 + ( λ a 13 + a 23 ) x 3 \left(\lambda a_{11}+a_{21}\right) x_1+\left(\lambda a_{12}+a_{22}\right) x_2+\left(\lambda a_{13}+a_{23}\right) x_3 ( λ a 11 + a 21 ) x 1 + ( λ a 12 + a 22 ) x 2 + ( λ a 13 + a 23 ) x 3
( λ a 11 + a 21 ) c 1 + ( λ a 12 + a 22 ) c 2 + ( λ a 13 + a 23 ) c 3 = λ ( a 11 c 1 + a 12 c 2 + a 13 c 3 ) + a 21 c 1 + a 22 c 2 + a 23 c 3 = λ b 1 + b 2 . \begin{aligned}
& \left(\lambda a_{11}+a_{21}\right) c_1+\left(\lambda a_{12}+a_{22}\right) c_2+\left(\lambda a_{13}+a_{23}\right) c_3 \\
= & \lambda\left(a_{11} c_1+a_{12} c_2+a_{13} c_3\right)+a_{21} c_1+a_{22} c_2+a_{23} c_3=\lambda b_1+b_2 .
\end{aligned} = ( λ a 11 + a 21 ) c 1 + ( λ a 12 + a 22 ) c 2 + ( λ a 13 + a 23 ) c 3 λ ( a 11 c 1 + a 12 c 2 + a 13 c 3 ) + a 21 c 1 + a 22 c 2 + a 23 c 3 = λ b 1 + b 2 . 由此可见, x 1 = c 1 , x 2 = c 2 , x 3 = c 3 x_1=c_1, x_2=c_2, x_3=c_3 x 1 = c 1 , x 2 = c 2 , x 3 = c 3 x 1 = c 1 , x 2 = c 2 , x 3 = c 3 x_1=c_1, x_2=c_2, x_3=c_3 x 1 = c 1 , x 2 = c 2 , x 3 = c 3
( λ a 11 + a 21 ) c 1 + ( λ a 12 + a 22 ) c 2 + ( λ a 13 + a 23 ) c 3 = λ b 1 + b 2 , \begin{aligned}
& \left(\lambda a_{11}+a_{21}\right) c_1+\left(\lambda a_{12}+a_{22}\right) c_2+\left(\lambda a_{13}+a_{23}\right) c_3 \\
= & \lambda b_1+b_2,
\end{aligned} = ( λ a 11 + a 21 ) c 1 + ( λ a 12 + a 22 ) c 2 + ( λ a 13 + a 23 ) c 3 λ b 1 + b 2 , 即
λ ( a 11 c 1 + a 12 c 2 + a 13 c 3 ) + a 21 c 1 + a 22 c 2 + a 23 c 3 = λ b 1 + b 2 . \lambda\left(a_{11} c_1+a_{12} c_2+a_{13} c_3\right)+a_{21} c_1+a_{22} c_2+a_{23} c_3=\lambda b_1+b_2 . λ ( a 11 c 1 + a 12 c 2 + a 13 c 3 ) + a 21 c 1 + a 22 c 2 + a 23 c 3 = λ b 1 + b 2 . 又因为 a 11 c 1 + a 12 c 2 + a 13 c 3 = b 1 a_{11} c_1+a_{12} c_2+a_{13} c_3=b_1 a 11 c 1 + a 12 c 2 + a 13 c 3 = b 1
a 21 c 1 + a 22 c 2 + a 23 c 3 = b 2 . a_{21} c_1+a_{22} c_2+a_{23} c_3=b_2 . a 21 c 1 + a 22 c 2 + a 23 c 3 = b 2 . 故 x 1 = c 1 , x 2 = c 2 , x 3 = c 3 x_1=c_1, x_2=c_2, x_3=c_3 x 1 = c 1 , x 2 = c 2 , x 3 = c 3
定义2 线性方程组的系数所组成的矩阵称为该线性方程组的系数矩阵 (coefficient matrix).
设线性方程组为
{ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 , a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 , a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 , . . . ( 5 ) \left\{\begin{array}{l}
a_{11} x_1+a_{12} x_2+a_{13} x_3=b_1, \\
a_{21} x_1+a_{22} x_2+a_{23} x_3=b_2, \\
a_{31} x_1+a_{32} x_2+a_{33} x_3=b_3,
\end{array}\right. ...(5) ⎩ ⎨ ⎧ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 , a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 , a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 , ... ( 5 ) 则系数矩阵 是
A = ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) , \boldsymbol{A}=\left(\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right), A = a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 , 并且称矩阵
( a 11 a 12 a 13 b 1 a 21 a 22 a 23 b 2 a 31 a 32 a 33 b 3 ) \left(\begin{array}{lll|l}
a_{11} & a_{12} & a_{13} & b_1 \\
a_{21} & a_{22} & a_{23} & b_2 \\
a_{31} & a_{32} & a_{33} & b_3
\end{array}\right) a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 b 1 b 2 b 3 为线性方程组的增广矩阵 (augmented matrix). 设 x = ( x 1 , x 2 , x 3 ) T , b = ( b 1 , b 2 \boldsymbol{x}=\left(x_1, x_2, x_3\right)^{\mathrm{T}}, \boldsymbol{b}=\left(b_1, b_2\right. x = ( x 1 , x 2 , x 3 ) T , b = ( b 1 , b 2 b 3 ) T \left.b_3\right)^{\mathrm{T}} b 3 ) T
定义3 称满足方程组(5)的三元有序数组为这个三元线性方程组的一个解(solution), 表示为列向量形式 ξ = ( k 1 , k 2 , k 3 ) T \xi=\left(k_1, k_2, k_3\right)^{\mathrm{T}} ξ = ( k 1 , k 2 , k 3 ) T ξ \xi ξ 解向量 (solution vector).
例解线性方程组
{ x 1 − x 2 + x 3 = 1 , x 1 − x 2 − x 3 = 3 , 2 x 1 − 2 x 2 − x 3 = 3. \left\{\begin{array}{l}
x_1-x_2+x_3=1, \\
x_1-x_2-x_3=3, \\
2 x_1-2 x_2-x_3=3 .
\end{array}\right. ⎩ ⎨ ⎧ x 1 − x 2 + x 3 = 1 , x 1 − x 2 − x 3 = 3 , 2 x 1 − 2 x 2 − x 3 = 3. 解:这个线性方程组的增广矩阵为
( 1 − 1 1 1 1 − 1 − 1 3 2 − 2 − 1 3 ) , \left(\begin{array}{ccc|c}
1 & -1 & 1 & 1 \\
1 & -1 & -1 & 3 \\
2 & -2 & -1 & 3
\end{array}\right), 1 1 2 − 1 − 1 − 2 1 − 1 − 1 1 3 3 , 将第一行乘 -1 加到第二行, 再将第一行乘 -2 加到第三行, 得
( 1 − 1 1 1 0 0 − 2 2 0 0 − 3 1 ) , \left(\begin{array}{ccc|c}
1 & -1 & 1 & 1 \\
0 & 0 & -2 & 2 \\
0 & 0 & -3 & 1
\end{array}\right), 1 0 0 − 1 0 0 1 − 2 − 3 1 2 1 , 将第二行乘 ( − 3 2 ) \left(-\frac{3}{2}\right) ( − 2 3 ) ( − 1 2 ) \left(-\frac{1}{2}\right) ( − 2 1 )
( 1 − 1 1 1 0 0 1 − 1 0 0 0 − 2 ) , \left(\begin{array}{ccc|c}
1 & -1 & 1 & 1 \\
0 & 0 & 1 & -1 \\
0 & 0 & 0 & -2
\end{array}\right), 1 0 0 − 1 0 0 1 1 0 1 − 1 − 2 , 相应的方程组变为阶梯形方程组
{ x 1 − x 2 + x 3 = 1 x 3 = − 1 0 = − 2 \left\{\begin{aligned}
x_1-x_2+x_3 & =1 \\
x_3 & =-1 \\
0 & =-2
\end{aligned}\right. ⎩ ⎨ ⎧ x 1 − x 2 + x 3 x 3 0 = 1 = − 1 = − 2 x 1 , x 2 , x 3 x_1, x_2, x_3 x 1 , x 2 , x 3 0 = − 2 0=-2 0 = − 2
定义4 设 A = ( a i j ) m × n \boldsymbol{A}=\left(a_{i j}\right)_{m \times n} A = ( a ij ) m × n A \boldsymbol{A} A A \boldsymbol{A} A A \boldsymbol{A} A A \boldsymbol{A} A
从例 2 可以看到, 线性方程组的初等变换可以转化为对应增广矩阵的行初等变换. 矩阵行初等变换的表示形式如下.
(1)矩阵互换变换
将矩阵 A \boldsymbol{A} A i i i j j j A \boldsymbol{A} A
( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) → ( r 2 , r 3 ) ( a 11 a 12 a 13 a 31 a 32 a 33 a 21 a 22 a 23 ) . \left(\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right) \xrightarrow{\left(r_2, r_3\right)}\left(\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{31} & a_{32} & a_{33} \\
a_{21} & a_{22} & a_{23}
\end{array}\right) . a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 ( r 2 , r 3 ) a 11 a 31 a 21 a 12 a 32 a 22 a 13 a 33 a 23 . (2)矩阵倍法变换
用一个非零常数 k k k A \boldsymbol{A} A i i i A \boldsymbol{A} A
( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) → 3 r 2 ( a 11 a 12 a 13 3 a 21 3 a 22 3 a 23 a 31 a 32 a 33 ) . \left(\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right) \xrightarrow{3 r_2}\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
3 a_{21} & 3 a_{22} & 3 a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right) . a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 3 r 2 a 11 3 a 21 a 31 a 12 3 a 22 a 32 a 13 3 a 23 a 33 . (3)矩阵消法变换
用 k k k A \boldsymbol{A} A j j j i i i A \boldsymbol{A} A
( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) → 2 r 3 + r 1 ( a 11 + 2 a 31 a 12 + 2 a 32 a 13 + 2 a 33 a 21 a 22 a 23 a 31 a 32 a 33 ) . \left(\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right) \xrightarrow{2 r_3+r_1}\left(\begin{array}{ccc}
a_{11}+2 a_{31} & a_{12}+2 a_{32} & a_{13}+2 a_{33} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right) . a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 2 r 3 + r 1 a 11 + 2 a 31 a 21 a 31 a 12 + 2 a 32 a 22 a 32 a 13 + 2 a 33 a 23 a 33 . 例解线性方程组
{ 2 x 1 + x 2 + x 3 = 3 , 3 x 1 + 3 x 2 + x 3 = 0 , − 2 x 1 − x 2 + 2 x 3 = 6. \left\{\begin{array}{l}
2 x_1+x_2+x_3=3, \\
3 x_1+3 x_2+x_3=0, \\
-2 x_1-x_2+2 x_3=6 .
\end{array}\right. ⎩ ⎨ ⎧ 2 x 1 + x 2 + x 3 = 3 , 3 x 1 + 3 x 2 + x 3 = 0 , − 2 x 1 − x 2 + 2 x 3 = 6. 解:对线性方程组的增广矩阵作行初等变换, 将增广矩阵变换为阶梯形矩阵.
因此, 这个线性方程组的解为
{ x 1 = 1 , x 2 = − 2 , x 3 = 3. \left\{\begin{array}{l}
x_1=1, \\
x_2=-2, \\
x_3=3 .
\end{array}\right. ⎩ ⎨ ⎧ x 1 = 1 , x 2 = − 2 , x 3 = 3. 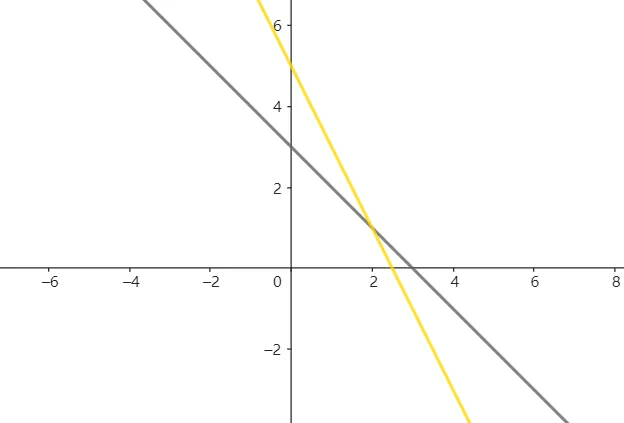 {width=300px}
{width=300px}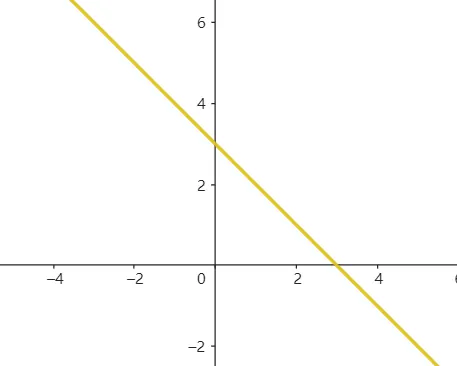 {width=300px}
可以看到,他们有重合,因此有无穷多个解。
事实上,第二个方程是第一个方程乘以2得到的,因此这两个方程最大的特点是系数成比例。
{width=300px}
可以看到,他们有重合,因此有无穷多个解。
事实上,第二个方程是第一个方程乘以2得到的,因此这两个方程最大的特点是系数成比例。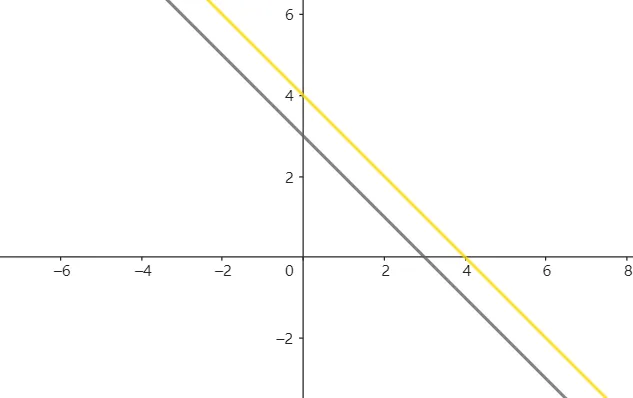 {width=300px}
可以看到他们是平行的,因此方程组无解。
事实上,第二个方程减去第一个方程的2倍,可以得到 这显然是矛盾的,因此方程组无解。
{width=300px}
可以看到他们是平行的,因此方程组无解。
事实上,第二个方程减去第一个方程的2倍,可以得到 这显然是矛盾的,因此方程组无解。