5._向量单位化 - Linear Algebra

向量长度的几何意义

如果 $x$ 是属于 $R ^n$ 的向量，其分量为 $x_1, \cdots, x_n$ ，因为 $x \cdot x$ 是非负数，那么 $x \cdot x$ 的平方根有意义。

向量 $x$ 的长度的定义为

\| x \|=\sqrt{ x \cdot x }=\sqrt{ x_1^2+ x_2^2+\cdots+ x_n^2}

二维向量长度的理解

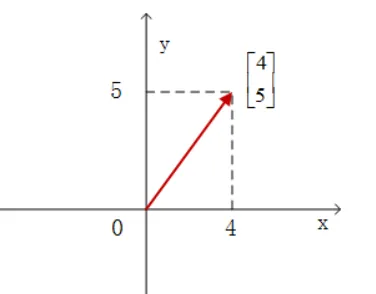
假若 $x$ 是 $R ^2$ 中的向量，且 $x=\left[\begin{array}{l}4 \\5 \end{array}\right]$ 。如果我们将 $x$ 与平面上的点 $(4, 5)$ 相对应，那么 $\| x\|$ 的值和平面内原点到点 $x$ 的线段长度一致, 即 $||x||=\sqrt{4^2+5^2}$

$图片$ {width=300px}

三维向量长度的理解

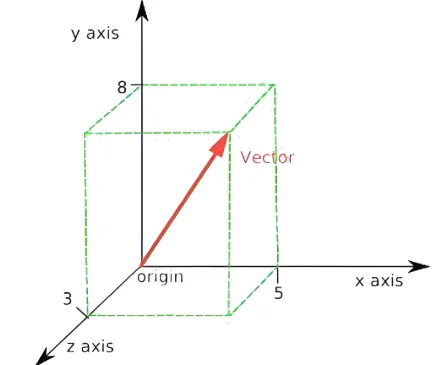
假若 $x$ 是 $R ^3$ 中的向量，且 $x=\left[\begin{array}{l}5 \\8 \\3 \end{array}\right]$ ，如果我们将 $x$ 与空间上的点 $(5, 8,3)$ 相对应，那么 $\| x\|$ 长度就是空间长方体对角形的长度，也就是 $||x||=\sqrt{5^2+8^2+3^2}$

$图片$

以此类推，可以得到 $n$ 维向量的长度。

$||x||=\sqrt{ x_1^2+ x_2^2+\cdots+ x_n^2}$

单位向量

模长（长度）为 1 的向量称为单位向量。如果把一个非零向量 $v$ 除以自身的长度, 即乘 $\frac{1}{\|v\|}$ , 就可以得到一个单位化的向量 $u$ 。这个过程称为向量 $v$ 的单位化, 且此时 $u$ 和 $v$ 方向一致. 即：单位化公式

\boxed{ u=\frac{1}{\|v\|} v ...\text{(向量单位化公式)} }

注意：向量模长就是向量的长度，既然是长度，所以他的值总是正的。

另外，规定零向量的模长为零。

例若 $v=(1,-2,2,0)$ , 找出他的单位向量 $u$ .

解：首先计算向量 $v$ 的模长,即各个分量的平方和再开方

\|v\|^2=v \cdot v=(1)^2+(-2)^2+(2)^2+(0)^2=9, \therefore \|v\|=\sqrt{9}=3

对 $v$ 乘 $\frac{1}{\| v \|}$ 得到

u=\frac{1}{\|v\|} v=\frac{1}{3} v=\frac{1}{3}\left[\begin{array}{r} 1 \\ -2 \\ 2 \\ 0 \end{array}\right]=\left[\begin{array}{c} 1 / 3 \\ -2 / 3 \\ 2 / 3 \\ 0 \end{array}\right]

例已知向量 $x=\left(\frac{2}{3}, 1\right)$ ，求他的单位向量

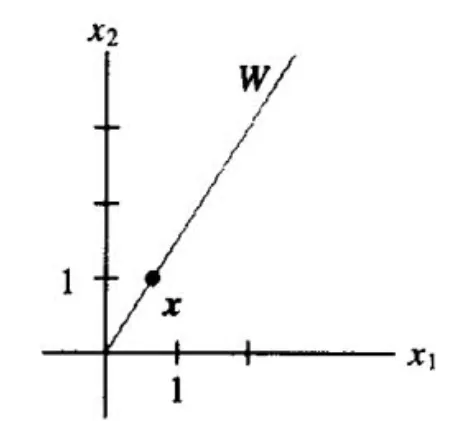
解：如图所示. 任何 $x$ 的非零倍都可以作为基向量，但是如果是单位向量还需要模为1. 为简化计算, 重新 "标度" $x$ 以消去分数。即向量 $x$ 乘 3 得到 $y =\left[\begin{array}{l}2 \\ 3\end{array}\right]$ , 现在计算 $\| y \|^2=2^2+3^2=13$ , $\|y\|=\sqrt{13}$ . 把向量 $y$ 单位化可得: $图片$ {width=200px}

单位向量为

y=\frac{1}{\sqrt{13}}\left[\begin{array}{l} 2 \\ 3 \end{array}\right]=\left[\begin{array}{l} \frac{2}{\sqrt{13}} \\ \frac{3}{\sqrt{13}} \end{array}\right]