3._线性函数_多项式_环与群 - Linear Algebra

线性函数的概念

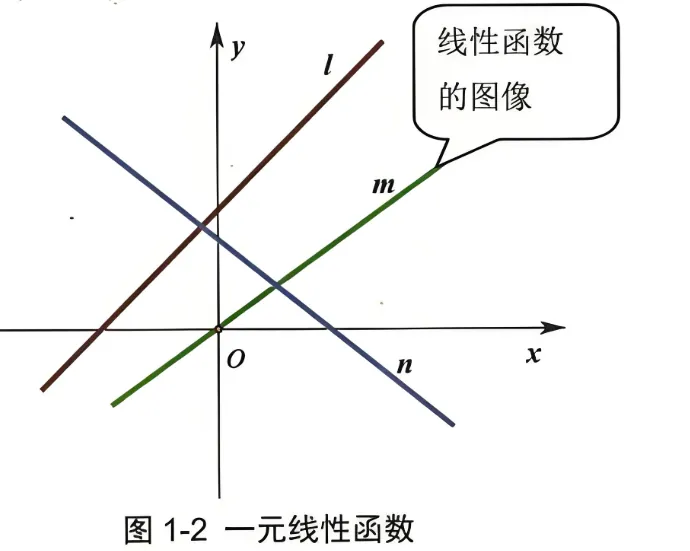
在中学的初等数学里, 我们知道, 函数 $f(x)=k x+b$ ( $k, b$ 是不变量), 称为一元线性函数, 因为在平面直角坐标系中这个函数的图形是一条直线, 就是变量 (包括自变量和因变量) 之间的关系描述为一条直线, 所以把这种函数形象地称为 “线性” 函数 (见图 1-2); 如果 $b=0$ , 这个函数的外观就变成 $f(x)=k x$ 的形式了, 这是一条过原点的直线, 即图中直线 $m$ 。显然, 过原点的直线是最简单的线性函数。

$图片$ {width=380px}

严格说来,只有过原点的最简单的直线 $f(x)=k x$ 才被称为一元线性函数。

什么? 难道 $f(x)=k x+b$ 不是线性函数吗? 是线性的, 但不是《线性代数》里所指的线性含义。

所谓 “线性” 的代数意义是什么呢? 实际上, 最基本的意义只有两条: 可加性和比例性。

(1) 可加性: 即如果函数 $f(x)$ 是线性的, 那么有

f\left(x_1+x_2\right)=f\left(x_1\right)+f\left(x_2\right)

一句话: 和的函数等于函数的和。物理意义是说因变量叠加后的作用结果等于各个因变量独自作用结果的叠加。

(2) 比例性: 也叫做齐次性、数乘性或均匀性或缩放性, 即如果函数 $f(x)$ 是线性的, 那么有

f(k x)=k f(x)

一句话: 比例的函数等于函数的比例。物理意义是说因变量缩放, 因变量的作用结果也同等比例地缩放。

可加性与比例性组合在一块就是 “线性” 的全部意义了, 即有

\boxed{ f\left(k_1 x_1+k_2 x_2\right)=k_1 f\left(x_1\right)+k_2 f\left(x_2\right) }

一句话: 线性组合的函数, 等于函数的线性组合。这里面既有缩放又有叠加的物理含义。

回过头来在说一下为什么说 $f(x)=kx+b$ 不是线性的，比如取 $f(x)=2x+4$ , 简单算一下， $f(1)=6$ $f(2)=8$ $f(3)=10$ ，

发现 $f(1)+f(2) \ne f(3)$ ，所以 $f(x)=2x+4$ 不算是线性代数里的线性。

但是，如果把他稍微修改一下（或者说图形平移一下）修改为 $g(x)=2x$ 就是线性的，

$g(x)=2x$ 满足

$g(1)+g(2)=g(3)$ $3g(x)=g(3x)$

进一步比较发现， $f(x)$ 和 $g(x)$ 的区别后者通过的原点。

到这里我们得到第一个重要结论：线性空间需要通过原点。

线性空间

上面说了，如果一个函数满足可加性和比例性，我们就称呼他为“线性”的。这是2个最主要的性质。

我们抽象一下，在一个集合 $V$ 里，定义了2个运算：加法与数乘，如果这2个运算的结果仍在 $V$ 中且满足下面列出的八条运算法则，那么就称一个 $V$ 的一个线性空间。

（1）加法交换律： $\alpha + \beta = \beta + \alpha$ ；（2）加法结合律： $(\alpha+\beta)+\gamma=\alpha+(\beta+\gamma)$ ；（3）存在零元素0：（3）存在单位元1：即 $k_1 \alpha = \alpha$ ；（5）存在负元素存在：即 $\alpha + \beta = 0$ ，称 $\beta$ 为 $\alpha$ 的负元素（6）数乘结合律： $k(l \alpha )=(k l) \alpha$ ；（7）分配律： $(k+l) \alpha =k \alpha +l \alpha$ ；（8）分配律： $k( \alpha + \beta )=k \alpha +k \beta$ ；

向量运算是线性的

在高中学过向量的加法和数乘，不难证明

\vec{a}+\vec{b}=\vec{b} + \vec{a} \\

\vec(ka)=k \vec{a} \\

所以，向量运算是线性的。

多项式是线性的

上面列出了线性空间的八条规则，换句话说，如果一个函数满足这八条规则，我们就称呼他是线性的，因为多项式满足这八条规则，所以，多项式也是线性的。 $\mathbf{F}[x]_{n+1}=\left\{a_0+a_1 x+\cdots+a_n x^n \mid a_i \in \mathbf{F}\right\}$ 关于多项式的加法和数乘构成线性空间，具体展开而言便是

\left(p_1+p_2\right)(x)=p_1(x)+p_2(x), \quad(\lambda p)(x)=\lambda p(x), \quad \forall p_1, p_2, p \in \mathbf{F}[x]_{n+1}, \quad \forall \lambda \in \mathbf{F} .

这也能解释常见记号的含义： $\left(k_1 p_1+k_2 p_2\right)(x)=k_1 p_1(x)+k_2 p_2(x)$ ．

我们对八条性质进行逐条验证即可． 1． $\forall p_1(x), p_2(x), p_3(x) \in \mathbf{F}[x]_{n+1}=\left\{a_0+a_1 x+\cdots+a_n x^n \mid a_i \in \mathbf{F}\right\}$ ，有

\begin{aligned} & \left(p_1(x)+p_2(x)\right)+p_3(x) \\ = & \left(\left(a_{10}+a_{11} x+\cdots+a_{1 n} x^n\right)+\left(a_{20}+a_{21} x+\cdots+a_{2 n} x^n\right)\right) + \left(a_{30}+a_{31} x+\cdots+a_{3 n} x^n\right) \\ = & \left(\left(a_{10}+a_{20}\right)+\left(a_{11}+a_{21}\right) x+\cdots+\left(a_{1 n}+a_{2 n}\right) x^n\right) + \left(a_{30}+a_{31} x+\cdots+a_{3 n} x^n\right) \\ = & \left(\left(\left(a_{10}+a_{20}\right)+a_{30}\right)+\left(\left(a_{11}+a_{21}\right)+a_{31}\right) x+\cdots+\left(\left(a_{1 n}+a_{2 n}\right)+a_{3 n}\right) x^n\right) \\ = & \left(\left(a_{10}+\left(a_{20}+a_{30}\right)\right)+\left(a_{11}+\left(a_{21}+a_{31}\right)\right) x+\cdots+\left(a_{1 n}+\left(a_{2 n}+a_{3 n}\right)\right) x^n\right) \\ = & \left(a_{10}+a_{11} x+\cdots+a_{1 n} x^n\right) + \left(\left(a_{20}+a_{21} x+\cdots+a_{2 n} x^n\right)+\left(a_{30}+a_{31} x+\cdots+a_{3 n} x^n\right)\right) \\ = & p_1(x)+\left(p_2(x)+p_3(x)\right) \end{aligned}

2．取定 $p_0(x)=0 \in V$ 则有 $\forall p(x) \in \mathbf{F}[x]_{n+1}, p(x)+p_0(x)=p_0(x)+p(x)$ ． 3.

\begin{aligned} & \forall p(x)=a_0+a_1 x+\cdots+a_n x^n \in \mathbf{F}[x]_{n+1}, \exists p^*(x)=-a_0-a_1 x-\cdots-a_n x^n \in \\ & \mathbf{F}[x]_{n+1}, p(x)+p^*(x)=p^*(x)+p(x)=p_0(x)=0 \end{aligned}

4． $\forall p_1(x), p_2(x) \in \mathbf{F}[x]_{n+1}$ 有

\begin{aligned} p_1(x)+p_2(x) & =\left(a_{10}+a_{11} x+\cdots+a_{1 n} x^n\right)+\left(a_{20}+a_{21} x+\cdots+a_{2 n} x^n\right) \\ & =\left(a_{10}+a_{20}\right)+\left(a_{11}+a_{21}\right) x+\cdots+\left(a_{1 n}+a_{2 n}\right) x^n \\ & =\left(a_{20}+a_{10}\right)+\left(a_{21}+a_{11}\right) x+\cdots+\left(a_{2 n}+a_{1 n}\right) x^n \\ & =\left(a_{20}+a_{21} x+\cdots+a_{2 n} x^n\right)+\left(a_{10}+a_{11} x+\cdots+a_{1 n} x^n\right) \\ & =p_2(x)+p_1(x) . \end{aligned}

5．取定 $\lambda=1 \in \mathbf{F}, \forall p(x) \in \mathbf{F}[x]_{n+1}, \lambda \cdot p(x)=p(x)$ ．

6． $\forall \lambda, \mu \in \mathbf{F}, p(x) \in \mathbf{F}[x]_{n+1}$ 有

\begin{aligned} \lambda(\mu p(x)) & =\lambda\left(\mu\left(a_0+a_1 x+\cdots+a_n x^n\right)\right)=\lambda\left(\mu a_0+\mu a_1 x+\cdots+\mu a_n x^n\right) \\ & =\lambda \mu a_0+\lambda \mu a_1 x+\cdots+\lambda \mu a_n x^n=(\lambda \mu)\left(a_0+a_1 x+\cdots+a_n x^n\right) \\ & =(\lambda \mu) p(x) \end{aligned}

7． $\forall \lambda, \mu \in \mathbf{F}, p(x) \in \mathbf{F}[x]_{n+1}$ 有

\begin{aligned} (\lambda+\mu) p(x) & =(\lambda+\mu)\left(a_0+a_1 x+\cdots+a_n x^n\right) \\ & =(\lambda+\mu) a_0+(\lambda+\mu) a_1 x+\cdots+(\lambda+\mu) a_n x^n \\ & =\lambda a_0+\mu a_0+\lambda a_1 x+\mu a_1 x+\cdots+\lambda a_n x^n+\mu a_n x^n \\ & =\lambda\left(a_0+a_1 x+\cdots+a_n x^n\right)+\mu\left(a_0+a_1 x+\cdots+a_n x^n\right) \\ & =\lambda p(x)+\mu p(x) \end{aligned}

这里的第二行到第三行并没有诉诸对单项式的分配律，而是利用了性质 6 和域 $\mathbf{F}$ 上的分配律．

8． $\forall p_1(x), p_2(x) \in \mathbf{F}[x]_{n+1}, \lambda \in \mathbf{F}$ 有

\begin{aligned} & \lambda\left(p_1(x)+p_2(x)\right) \\ = & \lambda\left(\left(a_{10}+a_{11} x+\cdots+a_{1 n} x^n\right)+\left(a_{20}+a_{21} x+\cdots+a_{2 n} x^n\right)\right) \\ = & \lambda\left(\left(a_{10}+a_{20}\right)+\left(a_{11}+a_{21}\right) x+\cdots+\left(a_{1 n}+a_{2 n}\right) x^n\right) \\ = & \lambda\left(a_{10}+a_{20}\right)+\lambda\left(a_{11}+a_{21}\right) x+\cdots+\lambda\left(a_{1 n}+a_{2 n}\right) x^n \\ = & \lambda\left(a_{10}+a_{11} x+\cdots+a_{1 n} x^n\right)+\lambda\left(a_{20}+a_{21} x+\cdots+a_{2 n} x^n\right) \\ = & \lambda p_1(x)+\lambda p_2(x) . \end{aligned}

现在我们整理一下：向量是线性的，多项式也是线性的，那是不是我们通过研究向量就能得出多项式的性质呢？或者反过来，通过研究多项式也能够知道向量的性质呢？答案是肯定的。

因此，在数学系的《高等代数》里，是把多项式和向量函数是一起进行研究的。

环

整数环

现在把上面的抽象在具体化，假设有一个整数集合，里面的元素满足下面的9种运算

1）加法满足结合律： $a+(b+c)=(a+b)+c$ ； 2）加法满足交换律： $a+b=b+a$ ； 3）有一个数 0 ，使对任意整数 $a, 0+a=a$ ； 4）对任一整数 $a$ ，存在整数 $b$ ，使 $b+a=0$ ； 5）乘法满足结合律： $a(b c)=(a b) c$ ； 6）有一个数 1 ，使对一切整数 $a$ ，有 $1 \cdot a=a$ ； 7）加法与乘法满足分配律： $a(b+c)=a b+a c$ ； 8）乘法满足交换律 $a b=b a$ ； 9）如果 $a \neq 0, b \neq 0$ ，则 $a b \neq 0$ ．

我们给他一个名字：有理整数环。

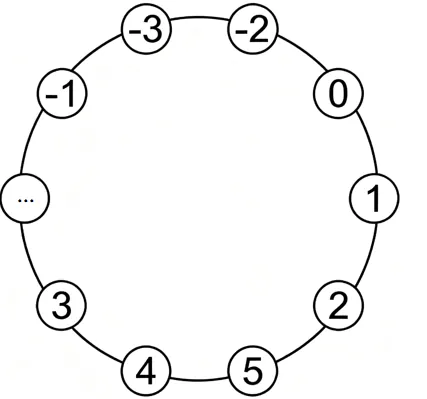
你可以想象一个闭合的环——在整数范围内加、减、乘，永远不会跑出这个圈。但除法会把你推出这个圈（可能得到分数），所以它只是“环”，不是“域”（域里除法畅通，除了除以零）。

$图片$ {width=300px}

理想

有了整数环，就可以对数进行分类，比如能被2整除的数叫做偶数，不能被2整除的数叫做奇数，这样整数就被分成了偶数和奇数，我们把分类后的集合称作理想。当然，分类可以由很多种方法，你也可以分为质数和合数等等。

对于偶数，两个偶数相加、相乘仍是偶数，满足交换律等，所以理想自己又构成了一个环。这条路走下去，就构造乘了算数定理，即每个整数都可以分解为质数的乘积。由此开启了通过代数研究数论。初等数论请参考初等数论

一元单项式环

考虑2个多项式

f(x)=a_0+a_1 x+a_2 x^2+\cdots 和 g(x)=b_0+b_1 x+b_2 x^2+\cdots

如果 $g(x)=f(x)h(x)$ 我们就说 $g(x)$ 能被 $f(x)$ 整除，通俗的说，就是 $g(x)$ 能被因式分解。例如

f(x)=x+1 和 g(x)=x^2-1

显然 $g(x)=f(x)(x-1)$ 这样对高次方程 $g(x)=0$ 的求解问题就转换为了多项式除法问题（降次）

假设有一个多项式 $f(a)=a_0 a^n+a_1 a^{n-1}+\cdots+a_n$ ，若 $f(a)=0$ ，则称 $x=a$ 是 $f(x)$ 的零点或根．

任给 $f(x)$ ，用 $x-a$ 去作带余除法：

f(x)=q(x)(x-a)+r

如果余数r=0,就表示多项式能整除。

重因式（重根）

在高次方程解里，重根是一个比较棘手的问题，或者你在求解矩阵特征值会能理解。让我们看一个例子：

$f(x) = (x - 2)³ * (x + 1)$ 这个多项式被分解成了两个“质因式”：

$(x - 2)$ ：它出现了 3 次。所以， $(x - 2)$ 就是 $f(x)$ 的一个 三重因式。
$(x + 1)$ ：它只出现了 1 次。所以， $(x + 1)$ 是 $f(x)$ 的一个 单因式。

对应的：方程 $f(x) = 0$ 在 $x = 2$ 处有一个 三重根（重根）。在 $x = -1$ 处有一个单根。

图像上的直观感受

重因式（重根）会显著影响函数图像的几何形状：

(x - a) 是一次（单因式）：
图像在 x = a 处穿过 x 轴。线条是倾斜的。

(想象一条斜线穿过x轴)

(x - a)² 是二次（二重因式）：
图像在 x = a 处接触 x 轴，并与 x 轴相切。线条在这里变得平坦。
例子：y = (x-1)² 是一个抛物线，顶点在 (1，0)。

(想象一个U型抛物线，底部刚好贴在x轴上)

(x - a)³ 是三次（三重因式）：
图像在 x = a 处穿过 x 轴，但同时也会有一个拐点（像一条蛇一样扭动着穿过x轴）。
例子：y = (x-1)³，它在 (1，0) 处穿过 x 轴，但不像斜线那样直接，而是像一个“S”形的中心点。

(想象一条曲线，在接触x轴时变得水平，然后继续延伸，像一个平缓的S)

简单总结：奇数次的重因式（1，3，5...）会穿过x轴，偶数次的重因式（2，4，6...）会接触并反弹回来。次数越高，在交点附近图像变得越“平坦”。

因此，重根个数能立刻告诉你函数图像在 x 轴交点处的行为（是穿过还是相切）。

总之，

重因式就是多项式“质因数分解”里出现的重复因子。它告诉你这个根在图像上是“一穿而过”还是“缠绵相切”，是理解多项式方程和函数图像行为的一个关键概念。下次看到 $(x - a)^n$ ，你就可以自信地说：“啊，这是一个 n 重因式，在 x=a 这个地方，图像会‘粘’在 x 轴上 n 次！”

群

设 $G$ 是一个非空集合，在 $G$ 内定义了一种代数运算，称为乘法，即定义了映射

\begin{aligned} G \times G & \rightarrow G, \\ (a, b) & \mapsto a b, \end{aligned}

且此乘法满足如下运算法则： 1）满足结合律，即对任意 $a, b, c \in G$ ，有 $a(b c)=(a b) c$ ； 2） $G$ 内存在一个元素 $e$ ，使对一切 $a \in G$ ，都有 $e a=a$ ； 3）对 $G$ 内任一元素 $a$ ，存在 $b \in G$ ，使 $b a=e$ ，则 $G$ 称为一个群．

群的出现，进一步抽象了代数的操作，此后，半群，李群等各种群都出现，关于群可以参考群论入门