35._矩阵的奇异值SVD分解

$A=U \Sigma V^{\mathrm{T}}$ 奇异值分解图解

包括长方阵在内的所有矩阵都具有奇异值分解（SVD）． $A=U \Sigma V^{\mathrm{T}}$ 中，有 $A$ 的奇异向量 $U$ 和 $V$ 。奇异值则排列在 $\Sigma$ 的对角线上．下图就是＂简化版＂的 SVD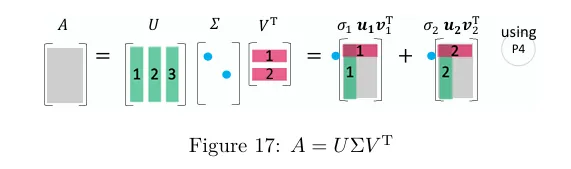． $图片$ 你可以发现， $V$ 是 $\mathbb{R}^n$ （ $A^{\mathrm{T}} A$ 的特征向量）的标准正交基，而 $U$ 是 $\mathbb{R}^m$ （ $A A^{\mathrm{T}}$ 的特征向量）的标准正交基．它们共同将 $A$ 对角化为 $\Sigma$ ．这也可以表示为秩 1 矩阵的线性组合．

$图片$

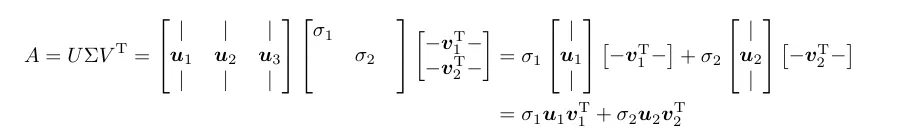
注意：

\begin{aligned} U U^{\mathrm{T}} & =I_m \\ V V^{\mathrm{T}} & =I_n \end{aligned}

矩阵的奇异值分解（Singular Value Decomposition, SVD），这是一个在数据科学、机器学习、信号处理、统计学等众多领域都非常重要且强大的工具。

1. 核心概念

SVD的核心思想是：任何一个矩阵，无论其形状（长方形或正方形）或性质（是否可逆），都可以被分解为三个特定矩阵的乘积。

对于一个 $m \times n$ 的实数矩阵 $A$ ，其SVD分解形式为： $A = U \Sigma V^T$

其中：

$U$ ：一个 $m \times m$ 的正交矩阵（Orthogonal Matrix）。
它的列向量称为左奇异向量（Left Singular Vectors）。
$U^TU = UU^T = I_m$ （ $I_m$ 是 $m \times m$ 的单位矩阵）。
$\Sigma$ ：一个 $m \times n$ 的矩形对角矩阵（Rectangular Diagonal Matrix）。
它的对角线上的元素称为奇异值（Singular Values），通常用 $\sigma_i$ 表示。这些值是非负的实数，并且通常按从大到小的顺序排列，即 $\sigma_1 \ge \sigma_2 \ge ... \ge \sigma_p \ge 0$ （其中 $p = \min(m, n)$ ）。
非对角线上的元素均为 0。
$V^T$ ：一个 $n \times n$ 的正交矩阵 $V$ 的转置。
$V$ 的列向量称为右奇异向量（Right Singular Vectors）。
$V^TV = VV^T = I_n$ 。

2. 几何解释（为什么SVD如此强大？）

从几何角度理解SVD非常直观。任何一个矩阵乘法 $A\vec{x}$ 都可以看作是一个线性变换：

旋转/反射（Rotation/Reflection）：首先，向量 $\vec{x}$ 与正交矩阵 $V^T$ 相乘，相当于在 $\mathbb{R}^n$ 空间中进行了一次旋转或反射。
缩放（Scaling）：然后，旋转后的向量与对角矩阵 $\Sigma$ 相乘。这相当于在各个坐标轴方向上进行缩放，缩放的倍数就是奇异值 $\sigma_i$ 。这是变换中最关键的一步，它可能将某些维度拉长，某些维度压缩，甚至压缩为0。
旋转/反射（Rotation/Reflection）：最后，缩放后的向量再与正交矩阵 $U$ 相乘，相当于在 $\mathbb{R}^m$ 空间中进行了一次旋转或反射。

所以，任何线性变换都可以分解为“旋转-缩放-旋转”这三步优雅的操作。

3. 如何计算SVD？（理论步骤）

计算SVD的过程与特征分解（Eigen Decomposition）紧密相关。

**计算 $A^TA$ 和 $AA^T$ **：

$A^TA$ 是一个 $n \times n$ 的对称半正定矩阵。
$AA^T$ 是一个 $m \times m$ 的对称半正定矩阵。

求 $A^TA$ 的特征值和特征向量：

计算 $A^TA$ 的特征值 $\lambda_i$ 和对应的单位特征向量 $\vec{v}_i$ 。
$A^TA$ 的特征值 $\lambda_i$ 都是非负的。其平方根就是矩阵 $A$ 的奇异值，即 $\sigma_i = \sqrt{\lambda_i}$ 。
所有这些特征向量 $\vec{v}_i$ 构成了正交矩阵 $V$ 的列。我们称 $V$ 为右奇异向量矩阵。

构造 $\Sigma$ 矩阵：

将计算出的奇异值 $\sigma_i$ 按从大到小的顺序排列，放在 $\Sigma$ 矩阵的对角线上。矩阵 $\Sigma$ 的尺寸为 $m \times n$ ，其余位置补零。

**求左奇异向量矩阵 $U$ **：

有两种方法：
方法一（常用）：利用公式 $\vec{u}_i = \frac{1}{\sigma_i} A \vec{v}_i$ （对于所有 $\sigma_i > 0$ 的 $i$ ）来求 $U$ 的前 $r$ 列（ $r$ 是 $A$ 的秩，即非零奇异值的个数）。对于 $\sigma_i = 0$ 的情况，需要通过求解 $AA^T \vec{u}_i = \vec{0}$ 来补齐 $U$ 的剩余列，并确保 $U$ 是正交矩阵。
方法二： $AA^T$ 的特征向量直接构成了 $U$ 的列。 $AA^T$ 的特征值同样也是 $\lambda_i$ （或 $\sigma_i^2$ ）。

注意：在实际应用中，我们几乎从不手动计算SVD，而是使用现成的、高度优化的数值计算库（如NumPy, SciPy, LAPACK等）。

4. 精简SVD（Truncated / Reduced SVD）

全尺寸的SVD会生成很大的矩阵（尤其是 $U$ 和 $\Sigma$ ）。在实际应用中，我们经常使用精简SVD，它只保留非零的奇异值以及对应的奇异向量。

假设矩阵 $A$ 的秩为 $r$ （即非零奇异值的个数），则精简SVD为： $A = U_r \Sigma_r V_r^T$ 其中：

$U_r$ ：一个 $m \times r$ 的矩阵，由 $U$ 的前 $r$ 列组成。
$\Sigma_r$ ：一个 $r \times r$ 的对角矩阵。
$V_r^T$ ：一个 $r \times n$ 的矩阵，由 $V^T$ 的前 $r$ 行组成。

这大大减少了存储开销，是很多应用的基础。

5. 重要应用

SVD的应用极其广泛，以下是一些经典例子：

数据降维与主成分分析（PCA）：

PCA本质上就是数据的协方差矩阵的SVD。奇异值的大小代表了对应维度的重要性。通过只保留前 $k$ 个最大的奇异值和对应的奇异向量（即使用秩 $k$ 近似），可以实现数据从高维到低维的压缩，同时保留最主要的信息。

图像压缩：

一张灰度图像可以看作一个矩阵。对其进行SVD分解后，丢弃那些较小的奇异值（以及对应的奇异向量），只用前 $k$ 个奇异值来重构图像（ $A \approx U_{：，：k} \Sigma_{：k, ：k} V_{：，：k}^T$ ）。这样可以极大地减小存储空间，实现压缩。

推荐系统：

著名的协同过滤算法（如Netflix Prize比赛中使用的模型）的核心就是SVD（或其变种）。用户-评分矩阵非常稀疏，通过SVD可以发现用户和物品背后的潜在特征（Latent Features），从而预测用户对未评分物品的喜好。

求解线性方程组和伪逆（Moore-Penrose Pseudoinverse）：

对于不可逆或非方阵的矩阵 $A$ ，其伪逆 $A^+$ 可以通过SVD优雅地求出： $A^+ = V \Sigma^+ U^T$ 。
其中 $\Sigma^+$ 是通过对 $\Sigma$ 取倒数（非零元素），然后转置得到。这为求解最小二乘问题提供了最稳定的数值方法。

矩阵的低秩近似（Eckart–Young–Mirsky定理）：

SVD提供了在弗罗贝尼乌斯范数（Frobenius norm）或谱范数（Spectral norm）意义下最好的秩 $k$ 近似矩阵。这意味着用SVD做数据近似是理论上最优的。

总结

特性/概念	描述
分解形式	$A = U \Sigma V^T$
U (左奇异向量)	正交矩阵，列张成列空间
Σ (奇异值)	对角矩阵，非负实数，衡量每个维度的重要性
V^T (右奇异向量)	正交矩阵，行张成行空间
核心思想	任何线性变换都可分解为：旋转 -> 缩放 -> 旋转
关键应用	降维(PCA)、图像压缩、推荐系统、求解伪逆、矩阵低秩近似、去除噪声等

希望这个详细的解释能帮助你彻底理解SVD！