矩阵左乘是行变换
下面例子演示了左乘的意思,对于A×B=C,以B为静止的参照物
200010001123456789=2238561489 从结果看,可以得到一个结论:
一个矩阵B左乘一个矩阵A,相当于对矩阵B行进行了行变换。
记忆口诀:左乘是行变换,右乘是列变换
1. 第一个例子
考虑M1×B
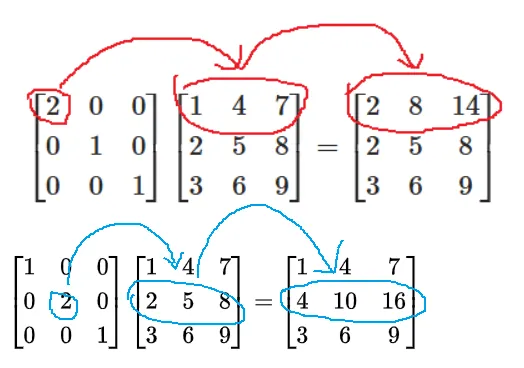
M1=200010001 左乘 B:
第 1 行变成 2×(第1行 of B)
第 2 行不变
第 3 行不变
这是对 B 的 行1 缩放 2 倍。
2. 第二个例子
考虑M2×B
M2=200310001 左乘 B:
新第 1 行 = 2×row1+3×row2
第 2、3 行不变
这是 行1 ← 2×行1 + 3×行2 的行线性组合。
3. 第三个例子
考虑M3×B
M3=230010001 左乘 B:
新第 1 行 = 2×row1
新第 2 行 = 3×row1+1×row2
第 3 行不变
这是 行1 缩放 与 行2 替换为 3×行1 + 行2。
4. 第四个例子
A×B=C:
230010001×123456789=253817614299 第1行 = 2×(B的第1行)
第2行 = 3× (B的第1行) +1× (B的第2行)
第3行 = B的第3行(不变)
求逆矩阵
因为这个关系,给你一个矩阵A,如果A可逆,那么通过初等行变换总能变成单位矩阵E,写成矩阵乘法就是:
Pk...P3P2P1⋅A=E 进一步的,因为A−1⋅A=E, 所以
A−1=Pk...P3P2P1 从上面可以得到逆矩阵的求法,
给你一个矩阵A,把他和单位矩阵E进行合并,然后使用行变换,左边化成E,则右边就是A−1
即
(A:E)→(E:A−1) 具体解释清参考 逆矩阵 ,他也是AX=B 方差的标准解法,见 逆矩阵解方程
矩阵左乘向量相当于改变观察视角(基变换)
考虑下面2个矩阵乘法,向量 α=(11) 变换成了 β=(02)
我们就说矩阵A作用在向量 α 上,使得 α 发生了伸缩和旋转变成了向量β
A(11−11)a(11)=b(02) 参考下图
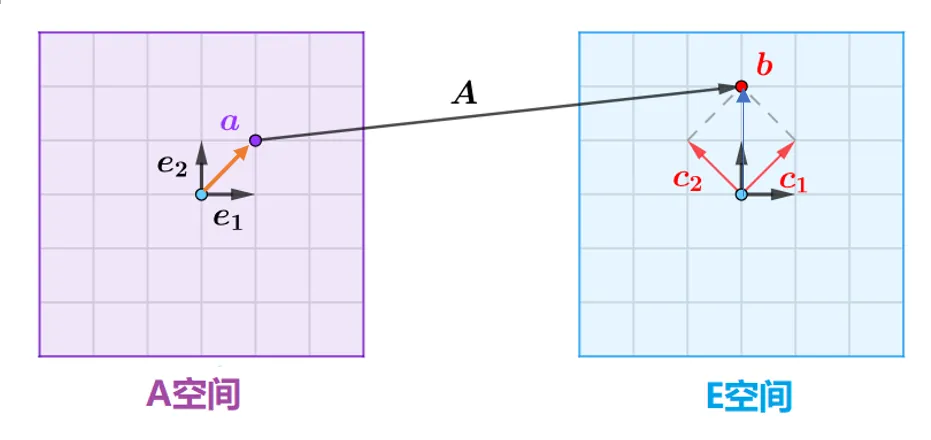
你可以这么理解:我在A空间里看到一个向量 α 换一个视角看他(笛卡尔坐标系),他变成了向量 β, 向量还是那个向量,因为观测角度不同,得到的向量就不通。
从物理上理解,在太空里有一个向量,我在地球上观察他是禁止的,但是如果我做飞船观察他,他是运动,造成这种不同的原因是我观察参照物变了。
矩阵左乘向量图解
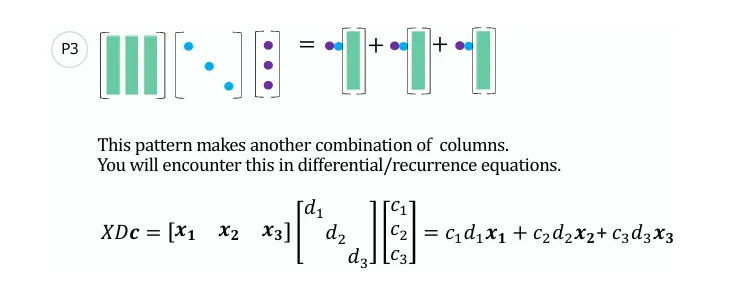
[x1x2x3]a11a21a31a12a22a32a13a23a33=x1[a11a12a13]+x2[a21a22a23]+x3[a31a32a33] 观察上式,用x行向量左乘矩阵 A ,相当于对矩阵 A 中的行向量做线性组合,线性组合的系数就是行向量 x 中的每个对应位置的元素。
矩阵右乘
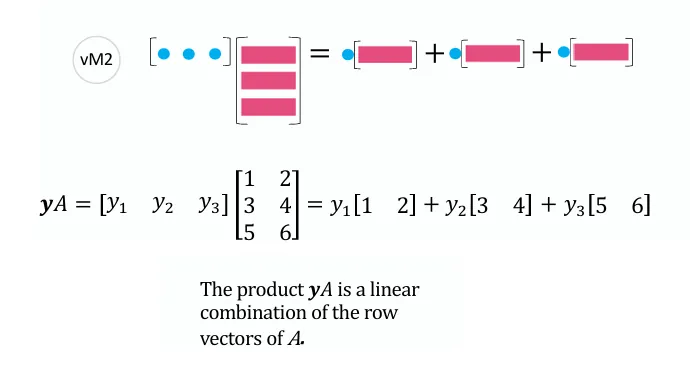
a11a21a31a12a22a32a13a23a33x1x2x3=x1a11a21a31+x2a12a22a32+x3a13a23a33 观察上式,不难发现,矩阵A右乘向量x 中的列向量 相当于对矩阵A的列做线性组合。
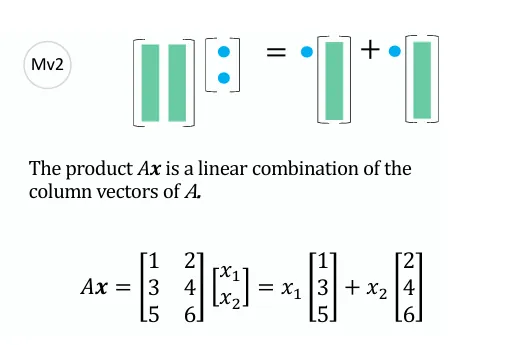
由此的下面定理
设 A 是一个 m×n 的矩阵,对 A 进行一次初等行变换相当于在 A 的左边乘一个相应类型的 m 阶初等矩阵;对 A 进行一次初等列变换相当于在 A 的右边乘一个相应类型的 n 阶初等矩阵.
矩阵乘以对角矩阵
右乘对角矩阵
矩阵右乘对角矩阵相当于对列乘积相应的倍数
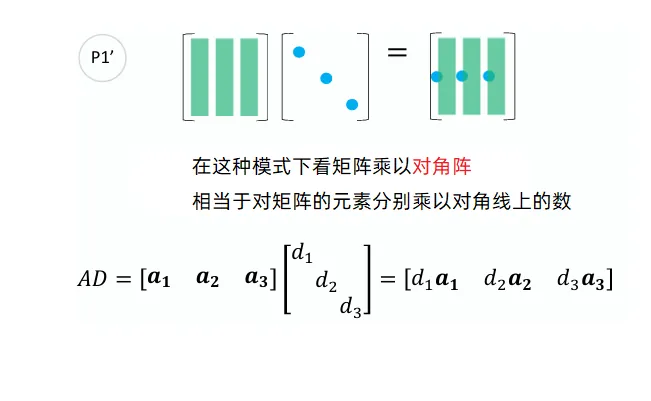
左乘对角矩阵
矩阵左乘对角矩阵相当于对行乘积相应的倍数
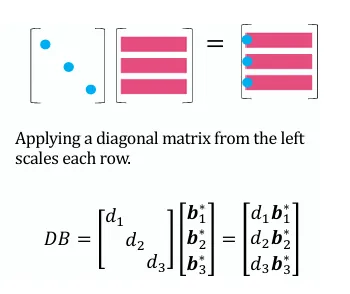
矩阵乘以对角矩阵和列向量
这种也可以看成列的组合。