27._雅可比矩阵及其行列式的几何意义

雅可比矩阵及其行列式的几何意义

因为雅可比矩阵如此重要且有趣, 雅可比矩阵是线性代数和微积分的纽带, 是把非线性问题转换为线性问题的有力工具之一。

雅可比矩阵及其行列式的几何意义

有一个函数方程组由 nn 个函数组成, 每个函数有 nn 个自变量 x1,x2,⋯ ,xnx_1, x_2, \cdots, x_n :

{y1=f1(x1,x2,⋯ ,xn)y2=f2(x1,x2,⋯ ,xn)⋮yn=fn(x1,x2,⋯ ,xn)\left\{\begin{array}{c} y_1=f_1\left(x_1, x_2, \cdots, x_n\right) \\ y_2=f_2\left(x_1, x_2, \cdots, x_n\right) \\ \quad \vdots \\ y_n=f_n\left(x_1, x_2, \cdots, x_n\right) \end{array}\right.

这个函数组有两个意义可以解释: 一个解释它是一个映射, 点 (x1,x2,⋯ ,xn)\left(x_1, x_2, \cdots, x_n\right) 被映射成 (y1,y2,⋯ ,yn)\left(y_1, y_2, \cdots, y_n\right); 另外的一个解释就是坐标变换的意思, 如果你把这个函数组代到一个以 y1,y2,⋯ ,yny_1, y_2, \cdots, y_n 为自变量的某方程中, 即相当于把某方程的原坐标系 {o,y1,y2,⋯ ,yn}\left\{o, y_1, y_2, \cdots, y_n\right\} 被替换成 {o,x1,x2,⋯ ,xn}\left\{o, x_1, x_2, \cdots, x_n\right\} 坐标系。这两个解释的本质是一回事, 是同一件事情从不同角度的看法。坐标系不动, 一个点被变换到另一个点, 这等价于说点不动, 一个坐标系被代换到另一个坐标系。 下面从其坐标变换的解释角度来分析。

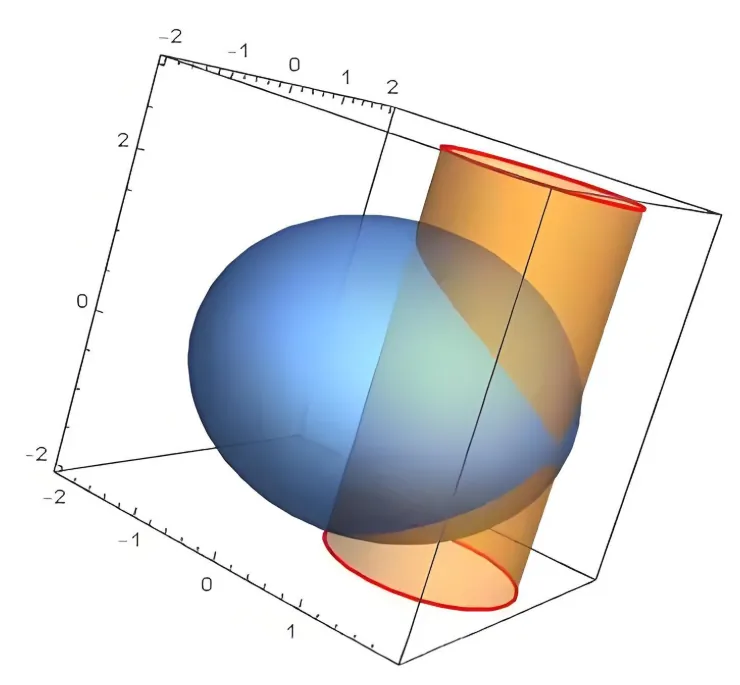
这里有2个结论：空间两个平面相交是直线，空间两个曲面相交是曲线。

比如一个椭球体和一个柱体相交，交痕就是一条曲线。 图片{WIDTH=300PX}

一般情况下, 这个函数方程组不是线性方程组, 它的图形多是高维曲线、曲面类的。稍详细一点说, 每一个函数是个超维曲面, nn 个超维曲面组合在一起交割成超维曲线。不过猛地看起来蛮像线性方程组的样子, 心里于是就有了把它弄成线性方程组的冲动: 弄成线性的可以使用矩阵、行列式啊什么的, 可以和线性变换联系起来, 多有几何意义啊。

咋弄成线性的? 直接改写成矩阵形式吗, 恐怕不行。嘿, 不是有微积分嘛, 微分就是把曲的弄成直的, 积分就是把直的弄成曲的。好, 对多元的非线性可微方程组进行偏微分:

{dy1=∂f1∂x1 dx1+∂f1∂x2 dx2+⋯+∂f1∂xn dxn dy2=∂f2∂x1 dx1+∂f2∂x2 dx2+⋯+∂f2∂xn dxn⋮dyn=∂fn∂x1 dx1+∂fn∂x2 dx2+⋯+∂fn∂xn dxn\left\{\begin{aligned} \mathrm{d} y_1 & =\frac{\partial f_1}{\partial x_1} \mathrm{~d} x_1+\frac{\partial f_1}{\partial x_2} \mathrm{~d} x_2+\cdots+\frac{\partial f_1}{\partial x_n} \mathrm{~d} x_n \\ \mathrm{~d} y_2 & =\frac{\partial f_2}{\partial x_1} \mathrm{~d} x_1+\frac{\partial f_2}{\partial x_2} \mathrm{~d} x_2+\cdots+\frac{\partial f_2}{\partial x_n} \mathrm{~d} x_n \\ & \vdots \\ \mathrm{d} y_n & =\frac{\partial f_n}{\partial x_1} \mathrm{~d} x_1+\frac{\partial f_n}{\partial x_2} \mathrm{~d} x_2+\cdots+\frac{\partial f_n}{\partial x_n} \mathrm{~d} x_n \end{aligned}\right.

到了这一步是不是和线性方程组有点相似了?! 这个过程就是激动人心之化曲为直的过程。几何意义上化每个超曲面为超平面 (函数 dyi=∂fi∂x1 dx1+∂fi∂x2 dx2+⋯+∂fi∂xn dxn\mathrm{d} y_i=\frac{\partial f_i}{\partial x_1} \mathrm{~d} x_1+\frac{\partial f_i}{\partial x_2} \mathrm{~d} x_2+\cdots+\frac{\partial f_i}{\partial x_n} \mathrm{~d} x_n 是超维切平面方程,因此实际上就是化为超维切平面), nn 个超平面组合在一起就是超维切线方程, 因此就这样化曲线为直线了。代数意义上就把高次函数方程组化成了齐次线性方程组。好, 那就把它写成矩阵的形式吧:

(dy1 dy2⋮dyn)=[∂f1∂x1∂f1∂x2⋯∂f1∂xn∂f2∂x1∂f2∂x2⋯∂f2∂xn⋮⋮⋮∂fn∂x1∂fn∂x2⋯∂fn∂xn](dx1 dx2⋮dxn′)...(5−17)\left(\begin{array}{c} \mathrm{d} y_1 \\ \mathrm{~d} y_2 \\ \vdots \\ \mathrm{d} y_n \end{array}\right)=\left[\begin{array}{cccc} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \cdots & \frac{\partial f_n}{\partial x_n} \end{array}\right]\left(\begin{array}{c} \mathrm{d} x_1 \\ \mathrm{~d} x_2 \\ \vdots \\ \mathrm{d} x_n^{\prime} \end{array}\right) ...(5-17)

当里个当, 主角雅可比矩阵出现了, 就是式(5-17)向量方程中间的大方块。当然雅可比行列式就是雅可比矩阵的行列式。册庸置疑, 雅可比矩阵和行列式具有前面讲过的矩阵和行列式的所有意义。除此之外, 还有两点特殊的地方:

一是向量的元素如 dx1、 dy1\mathrm{d} x_1 、 \mathrm{~d} y_1 等是微分, 它们是一些极小量, 而且是极小的向量; dxi\mathrm{d} x_i 是在 xix_i坐标轴上的微分向量, dyi\mathrm{d} y_i 是在 yiy_i 坐标轴上的微分向量。 二是雅可比矩阵里面的元素如 ∂f1∂x1、∂fn∂xn\frac{\partial f_1}{\partial x_1} 、 \frac{\partial f_n}{\partial x_n} 等一般不是常数, 而是变量, 这和前面讲的矩阵不同。

恰恰是这两点, 并结合矩阵的坐标系变换的意义, 我们终于揭开了雅可比矩阵和行列式的最终几何意义:

雅可比矩阵把一个超平面的仿射坐标系变换成了一个超曲面坐标系 ; 雅可比行列式就是曲面坐标系下单位微元和仿射坐标系下单位微元面积的比值。

不太明白, 再换一种说法:

雅可比矩阵把一个空间里的一个平面坐标系 ( 基 ) 变换成了无数个极小平面坐标系 ( 基 )；无数个极小平面就是曲面的切平面; 雅可比行列式就是切平面上每个坐标系下极小单位元和原坐标系下极小单位元面积的比值。

泛泛而谈让人昏昏入睡, 我们找个二维的具体例子看看吧。

雅可比矩阵在二重积分中的应用例子

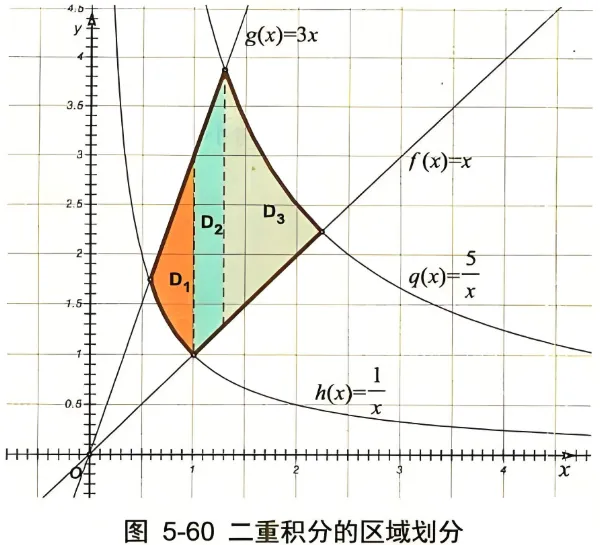
例计算二重积分 ∬D(y/x)2 dx dy\iint_D(y / x)^2 \mathrm{~d} x \mathrm{~d} y, 式中 DD 为由曲线 y=x,y=3x,xy=1,xy=5y=x, y=3 x, x y=1, x y=5 所围得第一象限部分的区域。

解：常规的解法是在默认的直角坐标系 {0,x,y,z}\{0, x, y, z\} 中进行积分, 其积分区域必须分为 D=D1+D2+D3D=D_1+D_2+D_3 三个区域 (见图 5-60)。先进行 dy\mathrm{d} y 积分, 然后再进行 dx\mathrm{d} x 积分。

图片{width=400px}

更简洁的解法是采用坐标变换法 {y/x=uxy=v\left\{\begin{array}{l}y / x=u \\ x y=v\end{array}\right. ，目的是把积分区域的边界化曲为直。颠倒自变量和因变量，得到坐标变换关系为 {x=v/uy=uv\left\{\begin{array}{l}x=\sqrt{v / u} \\ y=\sqrt{u v}\end{array}\right. ，这个变换函数组是非线性的，无法写成矩阵和向量的形式，对其进行偏微分，因此把变换写成雅可比矩阵形式为

(dx dy)=[−12uvu121uv12vu12uv](du dv)\binom{\mathrm{d} x}{\mathrm{~d} y}=\left[\begin{array}{cc} -\frac{1}{2 u} \sqrt{\frac{v}{u}} & \frac{1}{2} \frac{1}{\sqrt{u v}} \\ \frac{1}{2} \sqrt{\frac{v}{u}} & \frac{1}{2} \sqrt{\frac{u}{v}} \end{array}\right]\binom{\mathrm{d} u}{\mathrm{~d} v}

其雅可比行列式为

∣J∣=∣−12uvu121uv12vu12uv∣=−12u|J|=\left|\begin{array}{cc} -\frac{1}{2 u} \sqrt{\frac{v}{u}} & \frac{1}{2} \frac{1}{\sqrt{u v}} \\ \frac{1}{2} \sqrt{\frac{v}{u}} & \frac{1}{2} \sqrt{\frac{u}{v}} \end{array}\right|=-\frac{1}{2 u}

那么对应的积分区域 DD 的映像变为 D′={(u,v)∣1⩽u⩽3,1⩽v⩽5}D^{\prime}=\{(u, v) \mid 1 \leqslant u \leqslant 3,1 \leqslant v \leqslant 5\} ，而因积分变换为

∬D(y/x)2 dx dy=∬D′(y(u,v)/x(u,v))2∣J∣du dv=∬D′u2(−12u)du dv=−∫1312u du∫15 dv=−8\iint_D(y / x)^2 \mathrm{~d} x \mathrm{~d} y=\iint_{D^{\prime}}(y(u, v) / x(u, v))^2|\boldsymbol{J}| \mathrm{d} u \mathrm{~d} v=\iint_{D^{\prime}} u^2\left(-\frac{1}{2 u}\right) \mathrm{d} u \mathrm{~d} v=-\int_1^3 \frac{1}{2} u \mathrm{~d} u \int_1^5 \mathrm{~d} v=-8

雅可比行列式的绝对值问题

在这里我们没有取雅可比行列式的绝对值带入积分中, 因为这里自然地认为积分区域是有定向的, 雅可比行列式 ∣J∣=−12u|J|=-\frac{1}{2 u} 看起来为负值, 是因为微分向量 du, dv\mathrm{d} u, \mathrm{~d} v 叉积方向和 dk dy\mathrm{d} k \mathrm{~d} y 的叉积方向相反。但在本科生阶段, 因为没有引进外微分的概念, 总认为面积元 dx dy\mathrm{d} x \mathrm{~d} y 和 du dv\mathrm{d} u \mathrm{~d} v 是正的, 当然作为面积元比值的雅可比行列式也必须要求是正的了。所以你要考试的话老老实实地把雅可比行列式取绝对值吧。

好了, 先把例子的计算过程摆在上面, 下面我们就给出它对积分区域的坐标变换的几何解释。

首先看坐标变换前后的坐标系。图 5-61 (a) 是直角坐标系下的情形, 单位边长的浅色方块为单位面积元, 深色的以 dx dy\mathrm{d} x \mathrm{~d} y 为边长的小方块为面积微元 dx dy\mathrm{d} x \mathrm{~d} y, 这个面积微元可以要多小就有多小。因为 dx dy\mathrm{d} x \mathrm{~d} y 都是向量, 实际上这个面积微元是向量 dx\mathrm{d} x 和 dy\mathrm{d} y 的叉积, 因而是有向面积微元。

在经过坐标替换 {y/x=uxy=v\left\{\begin{array}{l}y / x=u \\ x y=v\end{array}\right. 后呢, 原来的直角-直线坐标系被替换成了直线一曲线坐标系: 直线 轴 是一簇经过原点的直线 {y/x=u∣u\{y / x=u \mid u 为不同的常数 }\}, 曲 线 轴 是一簇双曲线 {xy=v∣v\{x y=v \mid v 为不同的常数 }\}, 见图 5-61 (b)。

图片

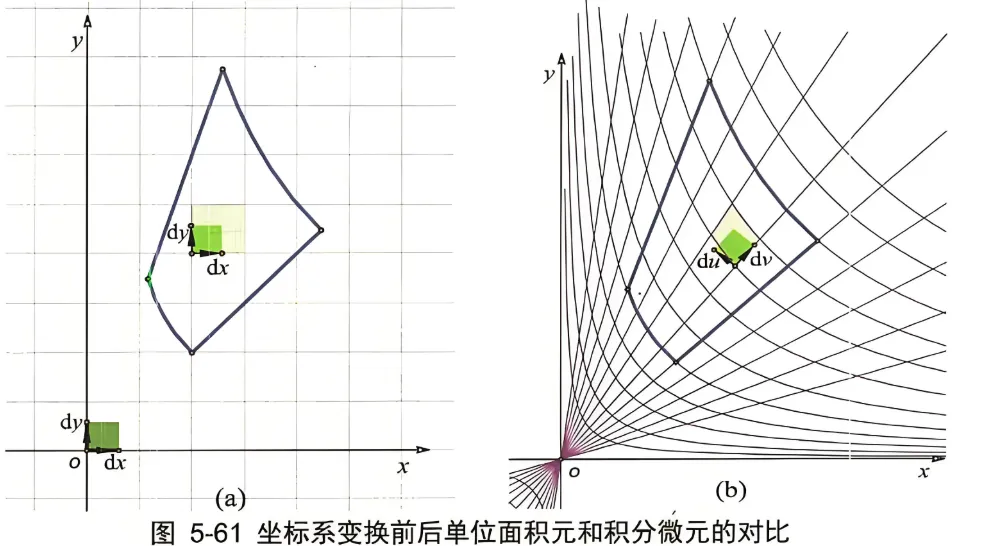
图 5-61 (b) 中坐标线所围成的浅色单位面积元是个曲线四边形, 它的面积微元 du dv\mathrm{d} u \mathrm{~d} v 是由过同一点的曲线的切线微分 du, dv\mathrm{d} u, \mathrm{~d} v 叉积张成的, 这是一个深色的小平行四边形, 要多小就有多小。因为 du dv\mathrm{d} u \mathrm{~d} v 都是向量, 因而也是有向面积微元。 面积微元 du dv\mathrm{d} u \mathrm{~d} v 的意思就是当这个曲线坐标轴的单位长度在取小极限时, 其曲边形的面积就等于两个曲线的切线段所张成的平行四边形的面积。

好了, 到了这里我们就知道了雅可比矩阵和行列式的几何意义:

二阶雅可比矩阵的几何意义就是把标准直角坐标系下的微分正方形 dx dy\mathrm{d} x \mathrm{~d} y 变换成了曲线坐标系下的微分平行四边形 du dv\mathrm{d} u \mathrm{~d} v;

二阶雅可比行列式的几何意义就是由标准直角坐标系下的微分正方形 dx dy\mathrm{d} x \mathrm{~d} y 所表示的面积微元变换到了曲线坐标系下的微分平行四边形 du dv\mathrm{d} u \mathrm{~d} v 所表示的面积微元之比率。

那么三阶雅可比的矩阵和行列式的几何意义可以类推为:

三阶雅可比矩阵的几何意义就是把标准直角坐标系下的微分立方体 dx dy dz\mathrm{d} x \mathrm{~d} y \mathrm{~d} z 变换成了曲线坐标系下的微分平行六面体 du dv dw\mathrm{d} u \mathrm{~d} v \mathrm{~d} w;

三阶雅可比行列式的几何意义就是由标准直角坐标系下的微分立方形 dx dy dz\mathrm{d} x \mathrm{~d} y \mathrm{~d} z 所表示的体积微元变换到了曲线坐标系下的微分平行六面体 du dv dw\mathrm{d} u \mathrm{~d} v \mathrm{~d} w 所表示的体积微元之比率。

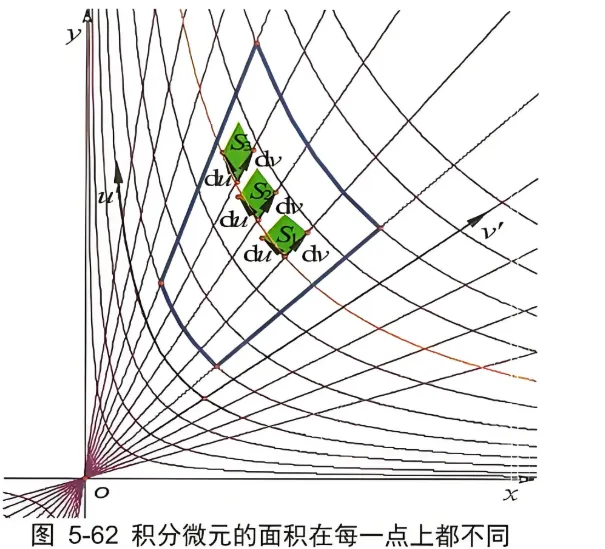
到了这里雅可比矩阵和行列式的几何意义基本就清楚了。但更有意思的和微分几何有深层联系的却是所谓的曲线坐标系。大家已经看出来了, 我们这里的曲线坐标系实际上被无数个仿射 (直线) 坐标系所替代或者模拟。因为随着积分区域内积分点的移动, 点上的沿着曲线的切线在变化 (方向在变换), 当然切线上的微分向量 du, dv\mathrm{d} u, \mathrm{~d} v 也在变化 (方向在变换), 由 du, dv\mathrm{d} u, \mathrm{~d} v 构成的仿射坐标轴 {du, dv}\{\mathrm{d} u, \mathrm{~d} v\} 也在变化, 也就是微分的仿射坐标系在不停地变换。

如图 5-62, 如果把整个积分区域的点遍历完毕, 将有无数个微小的仿射坐标系 {du, dv}\{\mathrm{d} u, \mathrm{~d} v\} 出现。当然仿射坐标的微分向量所张成的积分微元 (小平行四边形) 的大小或方向也在变化, 也就是雅可比行列式函数 ∣J∣=−12u|J|=-\frac{1}{2 u} 所给出或确定的。显然, 在曲线上随着 uu 值的变大点会向上移动, 点的切线顺时针旋转, 此点的另外一根切线方向不变, 因此 du dv\mathrm{d} u \mathrm{~d} v 的夹角变小, 所以积分微元的面积大小会变小, 也就是 ∣J∣|\boldsymbol{J}| 的绝对值会变小。

图片{WIDTH=400PX}

一句话, 就是因为雅可比矩阵行列式 ∣J∣=∣−12uvu121uv12vu12uv∣|\boldsymbol{J}|=\left|\begin{array}{cc}-\frac{1}{2 u} \sqrt{\frac{v}{u}} & \frac{1}{2} \frac{1}{\sqrt{u v}} \\ \frac{1}{2} \sqrt{\frac{v}{u}} & \frac{1}{2} \sqrt{\frac{u}{v}}\end{array}\right| 里面的元素是变量或函数, 所

以雅可比矩阵 JJ 实际上包含有无数个具体的变换矩阵, 随着点 (u,v)(u, v) 的改变, 此点附近的积分微元图形也被矩阵不停地变换着。

如果向更多理解他的意义请点击 复变函数导数雅可比行列式

Previous26._分块矩阵性质_逆与转置
Next28._平移矩阵_旋转矩阵_缩放矩阵_线性变换_仿射变换_齐次坐标