k 阶子式
我们已经知道, 行列式可以按任一列或任一行展开. 现在我们要将这个结论作进一步的推广. 首先引进 k 阶子式的概念.
设 ∣A∣ 是一个 n 阶行列式, k<n. 又 i1,i2,⋯,ik 及 j1,j2,⋯,jk是两组自然数且适合条件:
1≤i1<i2<⋯<ik≤n;1≤j1<j2<⋯<jk≤n 取行列式 ∣A∣ 中第 i1 行, 第 i2 行, ⋯, 第 ik 行以及第 j1 列, 第 j2 列, ⋯, 第 jk列交点上的元素, 按原来 ∣A∣ 中的相对位置构成一个 k 阶行列式. 我们称之为 ∣A∣的一个 k 阶子式, 记为
A(i1j1i2j2⋯⋯ikjk) 把这个子式写出来就是:
ai1j1ai2j1⋮aikj1ai1j2ai2j2⋮aikj2⋯⋯⋯ai1jkai2jk⋮aikjk. 在行列式 ∣A∣ 中去掉第 i1 行,第 i2 行, ⋯ ,第 ik 行以及第 j1 列,第 j2 列, ⋯ ,第 jk 列以后剩下的元素按原来的相对位置构成一个 n−k 阶行列式. 这个行列式称余子式, 记为
M(i1j1i2j2⋯⋯ikjk) 若令 p=i1+i2+⋯+ik,q=j1+j2+⋯+jk, 记
A(i1j1i2j2⋯⋯ikjk)=(−1)p+qM(i1j1i2j2⋯⋯ikjk) 称之为代数余子式.
我们这一节主要证明如下的 Laplace (拉普拉斯) 定理.
Laplace (拉普拉斯) 定理.
设 ∣A∣ 是 n 阶行列式,在 ∣A∣ 中任取 k 行 (列),那么含于这 k 行 (列) 的全部 k 阶子式与它们所对应的代数余子式的乘积之和等于 ∣A∣. 即若取定 k 个行: 1≤i1<i2<⋯<ik≤n, 则
∣A∣=1≤j1<j2<⋯<jk≤n∑A(i1j1i2j2⋯⋯ikjk)A(i1j1i2j2⋯⋯ikjk) 同样若取定 k 个列: 1≤j1<j2<⋯<jk≤n, 则
∣A∣=1≤i1<i2<⋯<ik≤n∑A(i1j1i2j2⋯⋯ikjk)A(i1j1i2j2⋯⋯ikjk) 例题
上面的定理很抽象,下面通过一个例题进行讲解。
例设有下列四阶行列式,采用拉普拉斯定理进行求解。
17−222043−15613214 解:根据拉普拉斯定理,这是一个四阶行列式,所以,我们可以任取1到4阶子式进行展开。其中1阶展开也就是以前学过的行列式展开模式, 所以,我们采用2阶子式来计算本题。
第一步:这是一个4解行列式,采用2阶子式时,可以任取两行进行处理,所以,我们固定第二、第三行,参考下图,
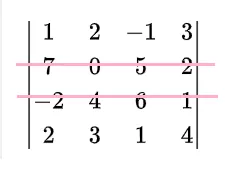
接下来找2列:则共有 C42(=6) 列,即
①取第一列第二列
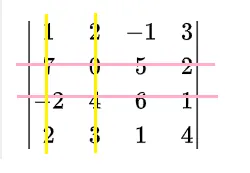 可以看到此时粉红线和深黄线交叉元素为
可以看到此时粉红线和深黄线交叉元素为
a1=7−204 而剩余的4个元素为余子式,即余子式为
M1=−1134 又因为交叉的4个元素的位置是第2行,第3行,第1列,第2列,所以,他的代数余子式为:
A1=(−1)2+3+1+2M1=(−1)2+3+1+2−1134 ②取第一列第三列
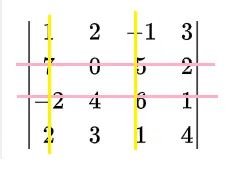
可以看到此时粉红线和深黄线交叉元素为
a2=7−256 而剩余的4个元素为余子式,即余子式为
M2=2334 又因为交叉的4个元素的位置是第2行,第3行,第1列,第3列,所以,他的代数余子式为:
A2=(−1)2+3+1+3M2=(−1)2+3+1+32334 用同样的方法
③ 取第一列第四列 可以得到a3,A3
④取第二列第三列,可以得到a4,A4
⑤取第二列第四列,可以得到a5,A5
⑥取第三列第四列,可以得到a6,A6
于是 Laplace 定理,整个行列式的值为
D=a1A1+a2A2+a3A3+a4A4+a5A5+a6A6 D===7−204−1134−7−2562334+7−22123−11+04561234−042112−11+5621122328×(−7)−52×(−1)+11×5+(−20)×(−2)−(−8)×3+(−7)×(−1)−18 当某 k 个行(列)中所含的 k 阶子式为零者甚多时,按这 k 行展开行列式,则计算量大为减少。
例 计算行列式
∣A∣=2100012100012100012100012 的值.
解 按前两行展开并去掉为零的项后得
∣A∣=2112(−1)1+2+1+2210121012+2101(−1)1+2+1+3100121012=3×4−2×3=6. 例用 Laplace 定理计算
D=a11⋮an1c11⋮cm1⋯⋯⋯⋯a1n⋮annc1n⋮cmn0⋮0b11⋮bm1⋯⋯⋯⋯0⋮0b1m⋮bmm ;
解 D 是一个 (m+n) 阶行列式.在前 n 行中,有后 m 列全为零元素。因此运用 Laplace 定理时,取 k=n ,且取定为前 n 行,则这 n 行中一切 n阶子式只有一个不为零.故
D=i=1∑tRiAi=R1⋅A1=a11⋮an1⋯⋯a1n⋮ann⋅(−1)(1+2+⋯+n)+(1+2+⋯+n)⋅b11⋮bm1⋯⋯b1m⋮bmm=a11⋮an1⋯⋯a1n⋮ann⋅b11⋮bm1⋯⋯b1m⋮bmm. 例用 Laplace 定理计算
D=0⋮0b11⋮bm1⋯⋯⋯⋯0⋮0b1m⋮bmma11⋮an1c11⋮cm1⋯⋯⋯⋯a1n⋮annc1n⋮cmn 解: D 也是一个 (m+n) 阶行列式 用 Laplace定理有
D=i=1∑tRiAi=a11⋮an1⋯⋯a1n⋮ann⋅(−1)(1+2+⋯+n)+[(m+1)+(m+2)+⋯+(m+n)]b11⋮bm1⋯⋯b1m⋮bmm=(−1)mn⋅a11⋮an1⋯⋯a1n⋮ann⋅b11⋮bm1⋯⋯b1m⋮bmm, 式中利用了 n(n+1) 必为偶数,因此 (−1)(m+n+1)⋅n=(−1)mn .
上面两个结果可以当做公式记
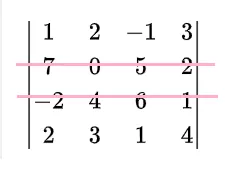
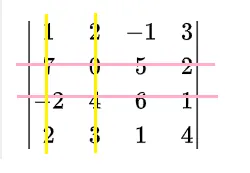 可以看到此时粉红线和深黄线交叉元素为
可以看到此时粉红线和深黄线交叉元素为