n 阶行列式的定义
由 n2 个元素 aij(i,j=1,2,⋯,n) 排成 n 行 n 列的正方形的数表:
Dn=a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann 由这个数表所决定的数 ∑p1p2⋯pn(−1)τ((p1⋯⋯pn)a1p1a2p2⋯anpn
称为由 n2 个元素 ay(i,j=1,2,⋯,n) 构成的 n 阶行列式,
对所有的 n 阶全排列 p1p2⋯pn 求和
①∑p1p2...pn 是对所有的 n 阶全排列 p1p2⋯pn 求和,所以展开式中共有 n! 项;
②每一项 a1p1a2p2⋯anpn 是取自不同行不同列的 n 个元素的乘积;
③每一项 a1p1,a2p2⋯anpn 的行标排成一个标准排列, 列标排列 p1p2⋯pn 的奇偶性决定了乘积a1p1,a2p2⋯anpn 前的符号.
这里给出了n阶行列式的定义与计算,估计很多同学看到定义都蒙了,别急,后面会用三阶行列式展开来告诉你如何理解定义。
记矩阵
A=a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann, 则行列式Dn通常也称为方阵 A 的行列式,记为 ∣A∣.
有时为了表明行列式是由元素 aij 构成的,也简记为 ∣A∣=det(aij)、∣aij∣n×n 或 ∣aij∣n.
根据上面定义计算三阶行列式
上面给出了n阶行列式的定义,比较抽象,这里以 n=3 为例,详细介绍行列式怎么取数和计算。 三阶行列式的定义如下
a11a21a31a12a22a32a13a23a33=p1p2p3∑(−1)τ(p1p2p3)a1p1a2p2a3p3 如何理解上式等号右边的式子? 首先,∑ 表示求和,这个大家都能看懂,齐次,τ(p1p2p3) 代表 (p1p2p3) 形成你逆序数,见逆序数教程
下面解释怎么取数
在等号右边求和里,即 a1p1a2p2a3p3 里可以看到 a的第一个下标都是固定的,变的只是p1,p2,p3
比如,取 p1=1,p2=2,p3=3,带入就是 a11a22a33,为了记录方便,可以写成 p1p2p3=123,代表取数 a11a22a33
同理,取 p1=1,p2=3,p3=2,带入就是 a11a23a32 , 也就是p1p2p3=132 代表取数是 a11a23a32
从这些取数里可以发现,每次取数时,第一个行标不变,而只变列标,这样,防止取数重复或者漏取。
再仔细看一下取数,每次取数时,这个数都是在不同行不同列上取的,比如我第一个数取a11 那么后面所有的数都不可能在第1行第1列取数,记住这个规律非常重要。
现在开始计算三阶行列式
STEP1:
根据定义, 3!=6,所以三阶行列式是共有6项,同时每项含有3个数相乘,这是大方向,不能搞错。
STEP2:
①p1p2p3=123 时, 对应项为
(−1)τ(123)a11a22a33=(−1)0a11a22a33=a11a22a33, ②p1p2p3=132 时, 对应项为
(−1)τ(132)a11a23a32=(−1)1a11a23a32=−a11a23a32, ③p1p2p3=213 时, 对应项为
(−1)τ(213)a12a21a33=(−1)1a12a21a33=−a12a21a33, ④p1p2p3=231 时, 对应项为
(−1)τ(231)a12a23a31=(−1)2a12a23a31=a12a23a31, ⑤p1p2p3=312 时, 对应项为
(−1)τ(312)a13a21a32=(−1)2a13a21a32=a13a21a32, ⑥p1p2p3=321 时, 对应项为
(−1)τ(321)a13a22a31=(−1)3a13a22a31=−a13a22a31 STEP3: 把这六项求和, 就得到三阶行列式
a11a21a31a12a22a32a13a23a33=p1p2p3∑(−1)τ(p1p2p3)a1p1a2p2a3p3=a11a22a33−a11a23a32−a12a21a33+a12a23a31+a13a21a32−a13a22a31 利用定义,不管是四阶行列式还是五阶行列式都可以采用这种思路计算。
n 阶行列式的性质
性质 1
行列式 Dn 与它的转置行列式 Dn⊤ 相等.
性质2
互换行列式的两行(或两列),行列式变号. 记为 ri↔rj 或 ci↔cj
172354461=−127345416,172354461=−461354172 性质3
若行列式中有两行 (或两列) 对应元素相等,则行列式等于零.
性质4
若行列式的某一行有公因子k ,则公因子k可以提到行列式记号外面;
这条性质必须和矩阵的区别出来,矩阵的是性质是 若矩阵里每个元素有公因子k ,则公因子k可以提到矩阵的记号外面;
性质5
设 D 是 n 阶方阵,则等式 ∣kD∣=kn∣D∣ 成立.
性质6 若行列式中某行 (列) 元素均为两项之和, 则行列式可表示为两个行列式之和。
性质7 行列式的某一行 (列) 乘以某个数加到另一行 (列) 上, 行列式的值不变。
三阶行列式的计算
例设 D=1−31232−21−1, 求 D.
解:可以化为上三角,也可以直接展开。
∣D∣=1−31232−21−1=1×3×(−1)+2×1×1+(−2)×(−3)×2−(−2)×3×1−1×1×2−2×(−3)×(−1)
=(−3)+2+12−(−6)−2−6=9.
四阶行列式的计算
对于超过3阶以上的行列式,通常需要使用行列式的性质,把他化为上三角或下三角进行计算。主要使用的一条性质是:性质7:行列式的某一行 (列) 乘以某个数加到另一行 (列) 上, 行列式的值不变。
例求四阶行列式
D=31221032−11410274 解:这是一个四阶行列式,主要利用行列式的性质,把他化成上三角。
①因为最终化为上三角,所以,我们希望第一行第一列最好都是1,然后用第一行消去第二行,用第一行消去第三行,用第一行消去第四行。为此,第二行和第一行互换,根据行列式性质,互换两行,行列式变号,前面需要添加一个负号。
Dr1↔r2−132201321−1412074 ②现在第一行不变,利用第一行分别消去第二行,第三行和第四行。行列式有一个性质是:一行的k倍加到另一行上去,行列式的值不变,因此
(i)第一行乘以 −3 加到第二行
(ii)第一行乘以 −2 加到第三行
(iii)第一行乘以 −2 加到第四行
D=−3r1+r2−2r1+r3−2r1+r4−100001321−42−12−630 ③ 现在第一列已经变成(k,0,0,0) 上三角形式了,
接下来处理第二列,让第二列由 (0,1,3,2) 变成 (a,b,0,0)形式, 为此,以第二行为基础,消去第三行和第四行。
(i)将第2行乘以 −3 加到第三行
(ii)将第2行乘以 −2 加到第四行
此时得到的行列式如下:
D−3r2+r3−2r2+r4−100001001−41472−62112 注意 在第一列已经处理完毕的情况下,第一列不再主动参与运算。比如第一行乘以一个数加到下面任何一行,都会破坏前面列已经化简的结果,但是从下往上被动是可以的,因为已经处理的列下面是0,0的倍数加上上面,值不变。
④观察上面第三行的数字是14和第四行的7,虽然14乘以−21 加到第四行可以销掉第四行,但是会产生分数,我们尽可能希望使用整数,因此 交换第三行和第四行(注意行列式再次变号),
Dr3↔r4100001001−47142−61221 然后用新的第3行乘以 −2 加到第四行上去。
D−2r3+r4−2100001001−4702−612−3 ⑤ 此时行列式已经化成上三角,结果是主对角线的值
100001001−4702−612−3=−21 对于任意一个四阶行列式,通过上述得变换,化简为上三角或下三角行列式,然后其值为主对角线的乘积。但是在具体算时,需要灵活运动行列的性质。
例计算
D=2354−3−24643−3−4542−5 解: 因为现 在a11=2 ,若将 a21,a31 化零时会出现分数。 我们要尽可能想办法让行列式中a11=1,(当然-1也可以) , 一种方法是第一行提取公因子法,即第一行提取一个公因子2,但是这样后面几个数字也会出现分数。
为此,先将 D 中第二 行的 −1 倍加到第一行上,使新的 a11=−1 .根据新的第 1 行的特点,将 a12,a13,a14 化为零更方便,
① 将第2行的-1倍加到第一行上,结果如下。 此时可以按照上一个例题用第一行消去第2,3,4 行,但是我们仔细观察数字,用第一列消去第2,3,4列更方便。总之,在化简过程中要保存两个原则,一是尽可能化为零,二是尽可能化为上三角或下三角,这2个主轴不能变。 根据结果要随时改变解题策略。
=−1354−1−24613−3−4142−5 ② 观察第一行后面3个数字,用第一列,消去第二列,用第一列消去第三列,用第一列消去第四列。
(i)第一列乘以−1 倍加到第二列
(ii)第一列乘以1 倍加到第三列
(iii)第一列乘以1 倍加到第四列 得
D=−13540−5−120620077−1, ③根据新行列式特点,拟将 D 化成下三角形行列式,

④需将 a23,a24,a34 化为零,因为a44=−1
所以
(i)用第四行的7倍加到第二行
(ii)用第四行的7倍加到第三行
得到如下行列式
D=−131334091320620000−1 ⑤接下来要把a23 化为零,
(i)用第三行的-3倍加到第二行
化成下三角后,行列式的值为辅对角线的值相乘即可。
=−1−683340−301320020000−1=(−1)×(−30)×2×(−1)=−60. 例题
例计算行列式
D=2111121111211112 解:注意到行列式的每一列元素之和都是 5 ,将行列式的第二、三、四行都加到第一行,得
D=5111521151215112=51111121111211112 r2+(−1)r1r3+(−1)r1r4+(−1)r51000110010101001=5 例计算n+1 阶行列式
Dn+1=c0b1b2⋮bna1c10⋮0a20c2⋮0⋯⋯⋯⋱⋯an00⋮cn,c1c2⋯cn=0 解 由题设知, c1,c2,⋯,cn 全不为零,依次给行列式 Dn+1 的第 2、第 3、 ⋯ 、第 n+1 列分别乘以 −c1b1,−c2b2,⋯,−cnbn 加到第 1 列, 由行列式的性质可得
所以,
Dn+1=c0−c1a1b1−c2a2b2−⋯−cnanbn00⋮0a1c10⋮0a20c2⋮0⋯⋯⋯⋱⋯an00⋮cn. Dn+1=(c0−c1a1b1−c2a2b2−⋯−cnanbn)c1c2⋯cn=(c0+k=1∑nckakbk)i=1∏nci 评注 这个行列式的特点是除第 1 行, 第 1 列和主对角线元素而外,其余元素均为零。它的所有非零元素组成一个汉字「爪」,所以,它也称为爪形行列式。由于有许多行列式可化为爪形行列式, 因此此类行列式化为三角形的方法应熟练掌握.
例计算行列式
D=a2b2c2d2(a+1)2(b+1)2(c+1)2(d+1)2(a+2)2(b+2)2(c+2)2(d+2)2(a+3)2(b+3)2(c+3)2(d+3)2 解 将行列式 D 中的第 1 列的 (-1) 倍加到第 2、3、4 列, 整理可得
D=a2b2c2d22a+12b+12c+12d+14a+44b+44c+44d+46a+96b+96c+96d+9 =a2b2c2d22a+12b+12c+12d+122226666=0 例 计算行列式
∣A∣=aaccbddbccaadbbd 的值.
解 将第二行的 (−1) 倍加到第一行,第四行的 (−1) 倍加到第三行得到
∣A∣=0a0cb−ddd−bb0c0ad−bbb−dd=0, 因为第一、三行成比例.
例 计算 n 阶行列式
∣D∣=abb⋮bbab⋮bbba⋮b⋯⋯⋯⋯bbb⋮a 的值.
解 行列式 ∣D∣ 的主对角线上的元全为 a ,其余的元全为 b .我们将第 2,3,⋯,n列都加到第一列上,然后提出第一列的公因子 a+(n−1)b ,得到
∣D∣=[a+(n−1)b]111⋮1bab⋮bbba⋮b⋯⋯⋯⋯bbb⋮a−1⋅(1) 行十 (i) 行 i=2,3,⋯,n[a+(n−1)b]100⋮0ba−b0⋮0b0a−b⋮0⋯⋯⋯⋯b00⋮a−b=[a+(n−1)b](a−b)n−1. n 阶行列式的几何意义
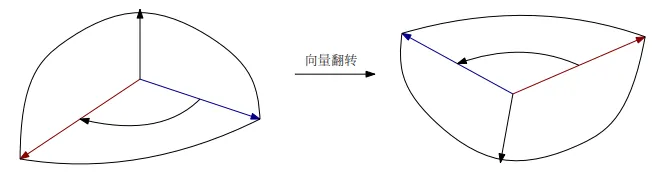
前面在介绍二阶行列式时,曾经说过,二阶行列式的值相当于在二维平面上两个向量形成的面积,在三阶行列式上,是三个向量形成的体积。以此类推,n 阶行列式的值为n个向量所张成的空间体积。
示意图如下
对于 n 维空间 n 个向量构成的多面体:
a1,⋯,ai,⋯,aj,⋯an, 记其体积为 D(a1,⋯,ai,⋯,aj,⋯an) 我们将其两个向量对换位置:
a1,⋯,aj,⋯,ai,⋯an, 记其体积为 D(a1,⋯,aj,⋯,ai,⋯an) 我们应当有:
D(a1,⋯,ai,⋯,aj,⋯an)=−D(a1,⋯,aj,⋯,ai,⋯an)