在矩阵等价里介绍了矩阵等价的定义,如果一个矩阵B = P A Q B=P A Q B = P A Q B ≃ A B \simeq A B ≃ A 此处 , 矩阵等价从方程的角度理解,反映的是“同解方程组 ”。从映射角度理解,矩阵等价意思是矩阵B B B A A A 但是根据定义,如何快速判断两个矩阵等价是一个比较棘手的问题 我们需要进一步寻找新的方法来解决这个问题,为此先引入向量组的等价。
向量组等价的定义 定义 设 A : α 1 , α 2 , ⋯ , α m A: \alpha_1, \alpha_2, \cdots, \alpha_m A : α 1 , α 2 , ⋯ , α m m m m n n n B : β 1 , β 2 , ⋯ , β s B: \beta_1, \beta_2, \cdots, \beta_s B : β 1 , β 2 , ⋯ , β s s s s n n n B B B β j ( j = 1 , 2 , ⋯ , s ) \beta_j(j=1,2, \cdots, s) β j ( j = 1 , 2 , ⋯ , s ) A : α 1 , α 2 , ⋯ , α m A: \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m A : α 1 , α 2 , ⋯ , α m B : β 1 , β 2 , ⋯ , β 3 B: \beta_1, \beta_2, \cdots, \beta_3 B : β 1 , β 2 , ⋯ , β 3 A : α 1 , α 2 , ⋯ , α m A: \alpha_1, \alpha_2, \cdots, \boldsymbol{\alpha}_m A : α 1 , α 2 , ⋯ , α m A A A B B B 相互线性表示 ,则称向量组 A A A B B B
向量等价的判定定理 设 A : α 1 , α 2 , ⋯ , α n A: \alpha_1, \alpha_2, \cdots, \alpha_n A : α 1 , α 2 , ⋯ , α n m m m n n n B : β , β , ⋯ , β B: \beta, \beta, \cdots, \beta B : β , β , ⋯ , β s s s n n n A = ( α 1 , α 2 , ⋯ , α n ) , B = ( β 1 , β 2 , ⋯ , β s ) A=\left(\alpha_1, \alpha_2, \cdots, \alpha_n\right) , B=\left(\beta_1, \beta_2, \cdots, \beta_s\right) A = ( α 1 , α 2 , ⋯ , α n ) , B = ( β 1 , β 2 , ⋯ , β s ) B B B A A A A X = B A X=B A X = B
证明:若向量组 B : β 1 , β 2 , ⋯ , β s B: \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_s B : β 1 , β 2 , ⋯ , β s A : α 1 , α 2 , ⋯ , α m A: \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m A : α 1 , α 2 , ⋯ , α m B B B β j ( j = 1 , 2 , ⋯ , s ) \beta_j(j=1,2, \cdots, s) β j ( j = 1 , 2 , ⋯ , s ) k 1 j , k 2 j , ⋯ , k m j k_{1 j}, k_{2 j}, \cdots, k_{m j} k 1 j , k 2 j , ⋯ , k mj
β j = k 1 j α 1 + k 2 j α 2 + ⋯ + k m j α m = ( α 1 , α 2 , ⋯ , α m ) ( k 1 j k 2 j ⋮ k m j ) ( j = 1 , 2 , ⋯ , s ) . \boldsymbol{\beta}_j=k_{1 j} \boldsymbol{\alpha}_1+k_{2 j} \boldsymbol{\alpha}_2+\cdots+k_{m j} \boldsymbol{\alpha}_m=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m\right)\left(\begin{array}{c}
k_{1 j} \\
k_{2 j} \\
\vdots \\
k_{m j}
\end{array}\right)(j=1,2, \cdots, s) . β j = k 1 j α 1 + k 2 j α 2 + ⋯ + k mj α m = ( α 1 , α 2 , ⋯ , α m ) k 1 j k 2 j ⋮ k mj ( j = 1 , 2 , ⋯ , s ) . 以向量 ( k 1 j k 2 j ⋮ k m j ) \left(\begin{array}{c}k_{1 j} \\ k_{2 j} \\ \vdots \\ k_{m j}\end{array}\right) k 1 j k 2 j ⋮ k mj m × s m \times s m × s
K m × s = ( k 11 k 12 ⋯ k 1 s k 21 k 22 ⋯ k 2 s ⋯ ⋯ ⋯ ⋯ k m 1 k m 2 ⋯ k m s ) . \boldsymbol{K}_{m \times s}=\left(\begin{array}{cccc}
k_{11} & k_{12} & \cdots & k_{1 s} \\
k_{21} & k_{22} & \cdots & k_{2 s} \\
\cdots & \cdots & \cdots & \cdots \\
k_{m 1} & k_{m 2} & \cdots & k_{m s}
\end{array}\right) . K m × s = k 11 k 21 ⋯ k m 1 k 12 k 22 ⋯ k m 2 ⋯ ⋯ ⋯ ⋯ k 1 s k 2 s ⋯ k m s . 矩阵 K m × s {K}_{m \times s} K m × s 系数矩阵 .
令矩阵 A = ( α 1 , α 2 , ⋯ , α m ) , B = ( β 1 , β 2 , ⋯ , β s ) A=\left(\alpha_1, {\alpha}_2, \cdots, {\alpha}_m\right) , B=\left(\beta_1, \beta_2, \cdots, \beta_s\right) A = ( α 1 , α 2 , ⋯ , α m ) , B = ( β 1 , β 2 , ⋯ , β s ) B = A K m × s B={A} {K}_{m \times s} B = A K m × s
也就是说,若向量组 B : β 1 , β 2 , ⋯ , β s \boldsymbol{B}: \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_s B : β 1 , β 2 , ⋯ , β s A : α 1 , α 2 , ⋯ , α m \boldsymbol{A}: \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m A : α 1 , α 2 , ⋯ , α m
有解 X = K m × s \boldsymbol{X}=\boldsymbol{K}_{m \times s} X = K m × s A \boldsymbol{A} A B \boldsymbol{B} B K m × s \boldsymbol{K}_{m \times s} K m × s M s × m \boldsymbol{M}_{s \times m} M s × m
B = A K m × s , B M s × m = A \boldsymbol{B}=\boldsymbol{A} \boldsymbol{K}_{m \times s}, \boldsymbol{B} \boldsymbol{M}_{s \times m}=\boldsymbol{A} B = A K m × s , B M s × m = A 同时成立.亦即矩阵方程
A X = B 与 B Y = A A X=B \text { 与 } B Y=A A X = B 与 B Y = A 同时有解 X = K m × s , Y = M s × m \boldsymbol{X}=\boldsymbol{K}_{m \times s}, \boldsymbol{Y}=\boldsymbol{M}_{s \times m} X = K m × s , Y = M s × m
例已知向量组 A : α 1 = ( 1 0 − 1 ) , α 2 = ( − 1 1 2 ) , α 3 = ( 1 2 5 ) A: \boldsymbol{\alpha}_1=\left(\begin{array}{c}1 \\ 0 \\ -1\end{array}\right), \boldsymbol{\alpha}_2=\left(\begin{array}{l}-1 \\ 1 \\ 2\end{array}\right), \boldsymbol{\alpha}_3=\left(\begin{array}{l}1 \\ 2 \\ 5\end{array}\right) A : α 1 = 1 0 − 1 , α 2 = − 1 1 2 , α 3 = 1 2 5 B : β 1 = ( 1 1 0 ) , β 2 = ( 0 1 1 ) , β 3 = ( 1 0 1 ) B: \boldsymbol{\beta}_1=\left(\begin{array}{l}1 \\ 1 \\ 0\end{array}\right), \boldsymbol{\beta}_2=\left(\begin{array}{l}0 \\ 1 \\ 1\end{array}\right), \boldsymbol{\beta}_3=\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right) B : β 1 = 1 1 0 , β 2 = 0 1 1 , β 3 = 1 0 1 A : α 1 , α 2 , α 3 A: \alpha_1, \alpha_2, \alpha_3 A : α 1 , α 2 , α 3 B : β 1 , β 2 , β 3 B: \beta_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 B : β 1 , β 2 , β 3
分析 :假设B B B A A A k k k
( 1 1 0 ) = β 1 = k 11 ( 1 0 − 1 ) + k 12 ( − 1 1 2 ) + k 13 ( 1 2 5 ) \left(\begin{array}{l}1 \\ 1 \\ 0\end{array}\right)=\boldsymbol{\beta}_1 =k_{11} \left(\begin{array}{c}1 \\ 0 \\ -1\end{array}\right) + k_{12} \left(\begin{array}{l}-1 \\ 1 \\ 2\end{array}\right) + k_{13} \left(\begin{array}{l}1 \\ 2 \\ 5\end{array}\right) 1 1 0 = β 1 = k 11 1 0 − 1 + k 12 − 1 1 2 + k 13 1 2 5 ( 0 1 1 ) = β 2 = k 21 ( 1 0 − 1 ) + k 22 ( − 1 1 2 ) + k 23 ( 1 2 5 ) \left(\begin{array}{l}0 \\ 1 \\ 1\end{array}\right)=\boldsymbol{\beta}_2=k_{21} \left(\begin{array}{c}1 \\ 0 \\ -1\end{array}\right) + k_{22} \left(\begin{array}{l}-1 \\ 1 \\ 2\end{array}\right) + k_{23} \left(\begin{array}{l}1 \\ 2 \\ 5\end{array}\right) 0 1 1 = β 2 = k 21 1 0 − 1 + k 22 − 1 1 2 + k 23 1 2 5 ( 1 0 1 ) = β 3 = k 31 ( 1 0 − 1 ) + k 32 ( − 1 1 2 ) + k 33 ( 1 2 5 ) \left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right)=\boldsymbol{\beta}_3 =k_{31} \left(\begin{array}{c}1 \\ 0 \\ -1\end{array}\right) + k_{32} \left(\begin{array}{l}-1 \\ 1 \\ 2\end{array}\right) + k_{33} \left(\begin{array}{l}1 \\ 2 \\ 5\end{array}\right) 1 0 1 = β 3 = k 31 1 0 − 1 + k 32 − 1 1 2 + k 33 1 2 5 上面可以表示为
( α 1 , α 2 , α 3 ) ( k 11 k 21 k 31 k 12 k 22 k 32 k 13 k 23 k 33 ) = ( β 1 , β 2 , β 3 ) (\boldsymbol{\alpha_1},\boldsymbol{\alpha_2},\boldsymbol{\alpha_3})
\left(\begin{array}{l} k_{11} \quad k_{21} \quad k_{31} \\
k_{12} \quad k_{22} \quad k_{32} \\
k_{13} \quad k_{23} \quad k_{33} \\
\end{array}\right) = (\boldsymbol{\beta_1},\boldsymbol{\beta_2},\boldsymbol{\beta_3})
( α 1 , α 2 , α 3 ) k 11 k 21 k 31 k 12 k 22 k 32 k 13 k 23 k 33 = ( β 1 , β 2 , β 3 ) 令矩阵 A = ( α 1 , α 2 , α 3 ) , B = ( β 1 , β 2 , β 3 ) A=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right) , B=\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3\right) A = ( α 1 , α 2 , α 3 ) , B = ( β 1 , β 2 , β 3 ) A K = B A \boldsymbol{K}=\boldsymbol{B} A K = B
即
因为我们要判断能否线性表示只要看方程有没有解即可,无需具体求出K K K 矩阵的秩与方程的解 的关系,但是作为例题,我们这里把具体的表达式求出来。
证明:
在上面使用A K = B AK=B A K = B B B B B X = A BX=A BX = A
对于B X = A BX=A BX = A B − 1 B^{-1} B − 1 X = B − 1 A X=B^{-1}A X = B − 1 A 逆矩阵解方程组
通过上面分析可以知道,要判断向量组等价,只要把两个向量组直接排列成增广矩阵,然后进行行初等变换,左边矩阵化为单位矩阵,然后判断矩阵的秩 。
( β 1 , β 2 , β 3 ∣ α 1 , α 2 , α 3 ) = ( 1 0 1 1 − 1 1 1 1 0 0 1 2 0 1 1 − 1 2 5 ) → ( 1 0 0 1 − 1 − 1 0 1 0 − 1 2 3 0 0 1 0 0 2 ) , \left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 \mid \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right)=\left(\begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & -1 & 1 \\
1 & 1 & 0 & 0 & 1 & 2 \\
0 & 1 & 1 & -1 & 2 & 5
\end{array}\right) \to \left(\begin{array}{ccc|ccc}
1 & 0 & 0 & 1 & -1 & -1 \\
0 & 1 & 0 & -1 & 2 & 3 \\
0 & 0 & 1 & 0 & 0 & 2
\end{array}\right), ( β 1 , β 2 , β 3 ∣ α 1 , α 2 , α 3 ) = 1 1 0 0 1 1 1 0 1 1 0 − 1 − 1 1 2 1 2 5 → 1 0 0 0 1 0 0 0 1 1 − 1 0 − 1 2 0 − 1 3 2 , 上面左边已经是单位矩阵,则右侧是方程的解。
矩阵方程 B X = A B X=A BX = A X = ( 1 − 1 − 1 − 1 2 3 0 0 2 ) \boldsymbol{X}=\left(\begin{array}{ccc}1 & -1 & -1 \\ -1 & 2 & 3 \\ 0 & 0 & 2\end{array}\right) X = 1 − 1 0 − 1 2 0 − 1 3 2 A A A B B B
∣ 1 − 1 − 1 − 1 2 3 0 0 2 ∣ = ∣ 1 − 1 − 1 0 1 2 0 0 2 ∣ = 2 ≠ 0 \left|\begin{array}{ccc}
1 & -1 & -1 \\
-1 & 2 & 3 \\
0 & 0 & 2
\end{array}\right|=\left|\begin{array}{ccc}
1 & -1 & -1 \\
0 & 1 & 2 \\
0 & 0 & 2
\end{array}\right|=2 \neq 0 1 − 1 0 − 1 2 0 − 1 3 2 = 1 0 0 − 1 1 0 − 1 2 2 = 2 = 0 所以矩阵 ( 1 − 1 − 1 − 1 2 3 0 0 2 ) \left(\begin{array}{ccc}1 & -1 & -1 \\ -1 & 2 & 3 \\ 0 & 0 & 2\end{array}\right) 1 − 1 0 − 1 2 0 − 1 3 2 A ( 1 − 1 − 1 − 1 2 3 0 0 2 ) − 1 = B \boldsymbol{A}\left(\begin{array}{ccc}1 & -1 & -1 \\ -1 & 2 & 3 \\ 0 & 0 & 2\end{array}\right)^{-1}=\boldsymbol{B} A 1 − 1 0 − 1 2 0 − 1 3 2 − 1 = B
即向量组 B B B A A A
如果仅证明向量组等价,还可以只用矩阵秩的方法进行判断,详见向量组等价的几何意义
例题 例已知向量组 A : α 1 = ( 1 1 − 1 ) , α 2 = ( − 2 0 1 ) A: \boldsymbol{\alpha}_1=\left(\begin{array}{l}1 \\ 1 \\ -1\end{array}\right), \boldsymbol{\alpha}_2=\left(\begin{array}{c}-2 \\ 0 \\ 1\end{array}\right) A : α 1 = 1 1 − 1 , α 2 = − 2 0 1 B : β 1 = ( 3 1 − 2 ) , β 2 = ( − 3 1 1 ) ⋅ β 3 = ( − 1 1 0 ) B: \beta_1=\left(\begin{array}{c}3 \\ 1 \\ -2\end{array}\right), \boldsymbol{\beta}_2=\left(\begin{array}{l}-3 \\ 1 \\ 1\end{array}\right) \cdot \boldsymbol{\beta}_3=\left(\begin{array}{l}-1 \\ 1 \\ 0\end{array}\right) B : β 1 = 3 1 − 2 , β 2 = − 3 1 1 ⋅ β 3 = − 1 1 0 B : β 1 , β 2 , β 3 B: \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 B : β 1 , β 2 , β 3 A : α 1 , α 2 A: \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2 A : α 1 , α 2
分析:
定理 要判断向量组A可以由向量组B表示或者向量组B可由向量组A表示只要判断R ( A ) = R ( B ) R(A)=R(B) R ( A ) = R ( B ) R ( A ) = R ( B ) = R ( A ∣ B ) R(A)=R(B)=R(A|B) R ( A ) = R ( B ) = R ( A ∣ B ) 向量组等价的几何意义
证明 令矩阵 A = ( α 1 , α 2 ) , B = ( β 1 , β 2 , β 3 ) A=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2\right) , B=\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3\right) A = ( α 1 , α 2 ) , B = ( β 1 , β 2 , β 3 )
现在把A B AB A B 初等行变换 (注意:此处只能做行变化),然后化为行最简形矩阵 ,判断矩阵的秩是否相等。
( α 1 , α 2 ∣ β 1 , β 2 , β 3 ) = ( 1 − 2 3 − 3 − 1 1 0 1 1 1 − 1 1 − 2 1 0 ) ∼ ( 1 0 1 1 1 0 1 − 1 2 1 0 0 0 0 0 ) , \left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2 \mid \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3\right)=\left(\begin{array}{cc|ccc}
1 & -2 & 3 & -3 & -1 \\
1 & 0 & 1 & 1 & 1 \\
-1 & 1 & -2 & 1 & 0
\end{array}\right) \sim \left(\begin{array}{cc|ccc}
1 & 0 & 1 & 1 & 1 \\
0 & 1 & -1 & 2 & 1 \\
0 & 0 & 0 & 0 & 0
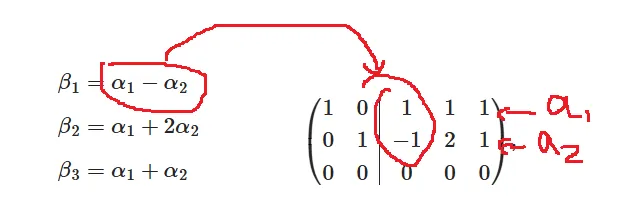
\end{array}\right), ( α 1 , α 2 ∣ β 1 , β 2 , β 3 ) = 1 1 − 1 − 2 0 1 3 1 − 2 − 3 1 1 − 1 1 0 ∼ 1 0 0 0 1 0 1 − 1 0 1 2 0 1 1 0 , 可见B B B A A A β 1 = α 1 − α 2 \beta_1=\alpha_1 - \alpha_2 β 1 = α 1 − α 2 β 2 = α 1 + 2 α 2 \beta_2=\alpha_1 +2 \alpha_2 β 2 = α 1 + 2 α 2 β 3 = α 1 + α 2 \beta_3=\alpha_1 + \alpha_2 β 3 = α 1 + α 2
如果你仔细看表达的系数恰好是矩阵右侧列向量的值,这不是偶然的,这是因为,向量组B可由向量组A表示就是解矩阵方程 B = A X B=AX B = A X A − 1 A^{-1} A − 1 X = A − 1 B X=A^{-1}B X = A − 1 B 逆矩阵求解方程组 里说过,要求X X X ( A ∣ B ) (A|B) ( A ∣ B ) A A A E E E X X X A X = B AX=B A X = B
X = ( 1 1 1 − 1 2 1 0 0 0 ) X=\left(\begin{array}{ccc}
& 1 & 1 & 1 \\
& -1 & 2 & 1 \\
& 0 & 0 & 0
\end{array}\right) X = 1 − 1 0 1 2 0 1 1 0 把A X = B AX=B A X = B
( α 1 , α 2 , α 3 ) ( 1 1 1 − 1 2 1 0 0 0 ) = ( β 1 , β 2 , β 3 ) (\boldsymbol{\alpha_1}, \boldsymbol{\alpha_2},\boldsymbol{\alpha_3})
\left(\begin{array}{ccc}
& 1 & 1 & 1 \\
& -1 & 2 & 1 \\
& 0 & 0 & 0
\end{array}\right)= (\boldsymbol{\beta_1}, \boldsymbol{\beta_2},\boldsymbol{\beta_3}) ( α 1 , α 2 , α 3 ) 1 − 1 0 1 2 0 1 1 0 = ( β 1 , β 2 , β 3 ) 展开就得到上图结果,即
β 1 = α 1 − α 2 β 2 = α 1 + 2 α 2 β 3 = α 1 + α 2 \begin{aligned}
& \beta_1=\alpha_1-\alpha_2 \\
& \beta_2=\alpha_1+2 \alpha_2 \\
& \beta_3=\alpha_1+\alpha_2
\end{aligned} β 1 = α 1 − α 2 β 2 = α 1 + 2 α 2 β 3 = α 1 + α 2 例 已知 3 维向量空间 R 3 R^3 R 3
a 1 = ( 1 1 1 ) , a 2 = ( 1 − 2 1 ) a_1=\left(\begin{array}{l}
1 \\
1 \\
1
\end{array}\right), a_2=\left(\begin{array}{r}
1 \\
-2 \\
1
\end{array}\right) a 1 = 1 1 1 , a 2 = 1 − 2 1 正交,试求一个非零向量 a 3 a_3 a 3 a 1 , a 2 , a 3 a_1, a_2, a_3 a 1 , a 2 , a 3
解 : 设所求向量为
a 3 = ( x 1 x 2 x 3 ) a_3=\left(\begin{array}{r}
x_1 \\
x_2 \\
x_3
\end{array}\right) a 3 = x 1 x 2 x 3 根据 向量内积 当垂直时,点积为零。所以
a 1 ⋅ a 3 = ( 1 1 1 ) ( x 1 x 2 x 3 ) = 0 展开为 x 1 + x 2 + x 3 = 0... ① a_1 \cdot a_3=
\left(\begin{array}{r}
1 \\
1 \\
1
\end{array}\right)
\left(\begin{array}{r}
x_1 \\
x_2 \\
x_3
\end{array}\right)=0 \text{展开为} x_1+x_2+x_3=0 ...① a 1 ⋅ a 3 = 1 1 1 x 1 x 2 x 3 = 0 展开为 x 1 + x 2 + x 3 = 0...① a 2 ⋅ a 3 = ( 1 − 2 1 ) ( x 1 x 2 x 3 ) = 0 展开为 x 1 + − 2 x 2 + x 3 = 0... ② a_2 \cdot a_3=
\left(\begin{array}{r}
1 \\
-2 \\
1
\end{array}\right)
\left(\begin{array}{r}
x_1 \\
x_2 \\
x_3
\end{array}\right)=0 \text{展开为} x_1+-2x_2+x_3=0 ...② a 2 ⋅ a 3 = 1 − 2 1 x 1 x 2 x 3 = 0 展开为 x 1 + − 2 x 2 + x 3 = 0...② 有①② 可以组成一个方程组
{ x 1 + x 2 + x 3 = 0 x 1 + − 2 x 2 + x 3 = 0 \left\{\begin{array}{r}
x_1+x_2+x_3=0 \\
x_1+-2x_2+x_3=0
\end{array}\right. { x 1 + x 2 + x 3 = 0 x 1 + − 2 x 2 + x 3 = 0 把方程写成矩阵相乘的形式,即
A = ( 1 1 1 1 − 2 1 ) , X = ( x 1 x 2 x 3 ) A = \left(\begin{array}{rrr}
1 & 1 & 1 \\
1 & -2 & 1
\end{array}\right),
X=\left(\begin{array}{rrr}
x_1 \\
x_2 \\
x_3
\end{array}\right) A = ( 1 1 1 − 2 1 1 ) , X = x 1 x 2 x 3 于是有
( 1 1 1 1 − 2 1 ) ( x 1 x 2 x 3 ) = ( 0 0 ) \left(\begin{array}{rrr}
1 & 1 & 1 \\
1 & -2 & 1
\end{array}\right)\left(\begin{array}{l}
x_1 \\
x_2 \\
x_3
\end{array}\right)=\binom{0}{0} ( 1 1 1 − 2 1 1 ) x 1 x 2 x 3 = ( 0 0 ) 把A化为最简形矩阵
A ∼ ( 1 1 1 0 − 3 0 ) ∼ ( 1 0 1 0 1 0 ) A \sim\left(\begin{array}{rrr}
1 & 1 & 1 \\
0 & -3 & 0
\end{array}\right) \sim\left(\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 0
\end{array}\right) A ∼ ( 1 0 1 − 3 1 0 ) ∼ ( 1 0 0 1 1 0 ) 如果把上面矩阵还原为方程组就是
x 1 + x 3 = 0 x 2 = 0 \begin{array}{l}
x_1+x_3=0 \\
x_2=0
\end{array}
x 1 + x 3 = 0 x 2 = 0 得 { x 1 = − x 3 x 2 = 0 \left\{\begin{array}{l}x_1=-x_3 \\ x_2=0\end{array}\right. { x 1 = − x 3 x 2 = 0
x 3 x_3 x 3 ( − 1 0 1 ) \left(\begin{array}{r}-1 \\ 0 \\ 1\end{array}\right) − 1 0 1 a 3 = ( − 1 0 1 ) a _3=\left(\begin{array}{r}-1 \\ 0 \\ 1\end{array}\right) a 3 = − 1 0 1
提示1:上面的解法可以参考 齐次方程的基础解系
提示2:后续如果熟悉的话,可以直接写出矩阵A为
A = ( a 1 T a 2 T ) = ( 1 1 1 1 − 2 1 ) , A =\binom{ a _1^{T}}{ a _2^{T}}=\left(\begin{array}{rrr}
1 & 1 & 1 \\
1 & -2 & 1
\end{array}\right), A = ( a 2 T a 1 T ) = ( 1 1 1 − 2 1 1 ) , 例 (考研训练)求常数 a a a α 1 = [ 1 , 1 , a ] T , α 2 = [ 1 , a , 1 ] T , α 3 = [ a , 1 , 1 ] T \alpha _1=[1,1, a]^{ T }, \alpha _2=[1, a, 1]^{ T }, \alpha _3=[a, 1,1]^{ T } α 1 = [ 1 , 1 , a ] T , α 2 = [ 1 , a , 1 ] T , α 3 = [ a , 1 , 1 ] T β 1 = [ 1 , 1 , a ] ⊤ , β 2 = [ − 2 , a , 4 ] ⊤ , β 3 = [ − 2 , a , a ] ⊤ \beta _1=[1,1, a]^{\top}, \beta _2=[-2, a, 4]^{\top}, \beta _3=[-2, a, a]^{\top} β 1 = [ 1 , 1 , a ] ⊤ , β 2 = [ − 2 , a , 4 ] ⊤ , β 3 = [ − 2 , a , a ] ⊤ β 1 , β 2 , β 3 \beta _1, \beta _2, \beta _3 β 1 , β 2 , β 3 α 1 , α 2 , α 3 \alpha _1, \alpha _2, \alpha _3 α 1 , α 2 , α 3
【解】 α 1 , α 2 , α 3 \alpha _1, \alpha _2, \alpha _3 α 1 , α 2 , α 3 β 1 , β 2 , β 3 \beta _1, \beta _2, \beta _3 β 1 , β 2 , β 3 r ( α 1 , α 2 , α 3 ) ⩽ r ( β 1 , β 2 , β 3 ) r\left( \alpha _1, \alpha _2, \alpha _3\right) \leqslant r\left( \beta _1, \beta _2, \beta _3\right) r ( α 1 , α 2 , α 3 ) ⩽ r ( β 1 , β 2 , β 3 ) β 1 , β 2 , β 3 \beta _1, \beta _2, \beta _3 β 1 , β 2 , β 3 α 1 , α 2 , α 3 \alpha _1, \alpha _2, \alpha _3 α 1 , α 2 , α 3 r ( α 1 , α 2 , α 3 ) < r ( β 1 , β 2 , β 3 ) r\left( \alpha _1, \alpha _2, \alpha _3\right)<r\left( \beta _1, \beta _2, \beta _3\right) r ( α 1 , α 2 , α 3 ) < r ( β 1 , β 2 , β 3 ) r ( β 1 , β 2 , β 3 ) ⩽ 3 r\left( \beta _1, \beta _2, \beta _3\right) \leqslant 3 r ( β 1 , β 2 , β 3 ) ⩽ 3 r ( α 1 r\left( \alpha _1\right. r ( α 1 α 2 , α 3 ) < 3 \left.\alpha _2, \alpha _3\right)<3 α 2 , α 3 ) < 3 ∣ α 1 , α 2 , α 3 ∣ = 0 \left| \alpha _1, \alpha _2, \alpha _3\right|=0 ∣ α 1 , α 2 , α 3 ∣ = 0 a = 1 a=1 a = 1 a = − 2 a=-2 a = − 2
当 a = 1 a=1 a = 1 α 1 = α 2 = α 3 = β 1 = [ 1 , 1 , 1 ] ⊤ \alpha _1= \alpha _2= \alpha _3= \beta _1=[1,1,1]^{\top} α 1 = α 2 = α 3 = β 1 = [ 1 , 1 , 1 ] ⊤ α 1 , α 2 , α 3 \alpha _1, \alpha _2, \alpha _3 α 1 , α 2 , α 3 β 1 , β 2 , β 3 \beta _1, \beta _2, \beta _3 β 1 , β 2 , β 3 β 2 = \beta _2= β 2 = [ − 2 , 1 , 4 ] ⊤ [-2,1,4]^{\top} [ − 2 , 1 , 4 ] ⊤ a 1 , a 2 , a 3 a _1, a _2, a _3 a 1 , a 2 , a 3 a = 1 a=1 a = 1
当 a = − 2 a=-2 a = − 2
[ 1 − 2 − 2 1 1 − 2 1 − 2 − 2 1 − 2 1 − 2 4 − 2 − 2 1 1 ] ∼ [ 1 − 2 − 2 1 1 − 2 0 0 − 6 0 3 − 3 0 0 0 0 − 3 3 ] \left[\begin{array}{ccc:ccc}
1 & -2 & -2 & 1 & 1 & -2 \\
1 & -2 & -2 & 1 & -2 & 1 \\
-2 & 4 & -2 & -2 & 1 & 1
\end{array}\right]
\sim
\left[\begin{array}{ccc:ccc}
1 & -2 & -2 & 1 & 1 & -2 \\
0 & 0 & -6 & 0 & 3 & -3 \\
0 & 0 & 0 & 0 & -3 & 3
\end{array}\right] 1 1 − 2 − 2 − 2 4 − 2 − 2 − 2 1 1 − 2 1 − 2 1 − 2 1 1 ∼ 1 0 0 − 2 0 0 − 2 − 6 0 1 0 0 1 3 − 3 − 2 − 3 3 可知 r ( β 1 , β 2 , β 3 ) = 2 r\left( \beta _1, \beta _2, \beta _3\right)=2 r ( β 1 , β 2 , β 3 ) = 2 r ( [ β 1 , β 2 , β 3 , α 2 ] ) = 3 r\left(\left[ \beta _1, \beta _2, \beta _3, \alpha _2\right]\right)=3 r ( [ β 1 , β 2 , β 3 , α 2 ] ) = 3 a 2 a _2 a 2 β 1 , β 2 , β 3 \beta _1, \beta _2, \beta _3 β 1 , β 2 , β 3 a = − 2 a=-2 a = − 2
综上所述,a = 1 a=1 a = 1
向量组等价的性质 向量组间的等价具有:
(1)反身性 .即每个向量组与它自身等价.
(2)对称性 .即若向量组(I) α 1 , α 2 , ⋯ , α \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha} α 1 , α 2 , ⋯ , α β 1 , β 2 , ⋯ , β \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta} β 1 , β 2 , ⋯ , β 传递性 .即若向量组(I) α 1 , α 2 , ⋯ , α s \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_s α 1 , α 2 , ⋯ , α s β 1 , β 2 , ⋯ , β 1 \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_1 β 1 , β 2 , ⋯ , β 1 β 1 , β 2 , ⋯ , β 1 \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_1 β 1 , β 2 , ⋯ , β 1 γ 1 , γ 2 , ⋯ , γ r \gamma_1, \gamma_2, \cdots, \gamma_{\text {r }} γ 1 , γ 2 , ⋯ , γ r
证明:略。
由传递性可见,向量组的线性表示是有传递性的,即若向量组 (I)可由向量组(II)线性表示,向量组(II)可由向量组(III)线性表示,则向量组( I )也可由向量组(III)线性表示.
常见问答 问:两个矩阵的等价与两个向量组的等价有什么区别和联系?
答 矩阵 A A A B B B A A A B B B A : α = A: \alpha = A : α = ( 1 1 ) \binom{1}{1} ( 1 1 ) B : { β = k ( 1 1 ) ∣ k ∈ R } B:\left\{\left. \beta =k\binom{1}{1} \right\rvert\, k \in R \right\} B : { β = k ( 1 1 ) k ∈ R }
两矩阵的等价与两向量组的等价两者的联系在于:
(1) 若矩阵 A A A B B B A A A B B B A A A B B B A A A C C C A A A C C C A A A C C C A A A D D D A A A D D D A A A D D D ⊕ \oplus ⊕ m m m n × m n \times m n × m n n n
向量组 A : ( 1 2 ) , ( 2 4 ) A:\binom{1}{2},\binom{2}{4} A : ( 2 1 ) , ( 4 2 ) B : ( 1 2 ) , ( 0 0 ) B:\binom{1}{2},\binom{0}{0} B : ( 2 1 ) , ( 0 0 ) A = A= A = ( 1 2 2 4 ) \left(\begin{array}{ll}1 & 2 \\ 2 & 4\end{array}\right) ( 1 2 2 4 ) B = ( 1 0 2 0 ) B =\left(\begin{array}{ll}1 & 0 \\ 2 & 0\end{array}\right) B = ( 1 2 0 0 ) A A A B B B
类似地, 若两个含向量个数相同的行向量组等价, 则它们对应的两矩阵行等价, 从而一定等价, 但不一定列等价.
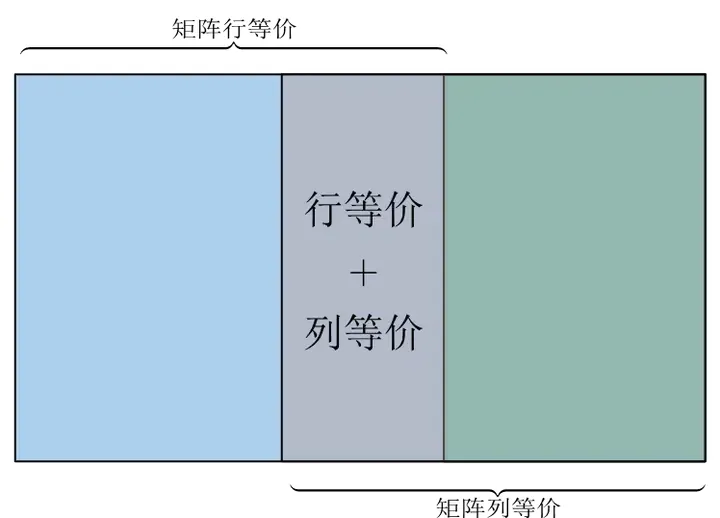
在同阶矩阵下,上面的结论大致可用下图表示
如果把矩阵等价看成是图中的整个大框,大框里面有两个小框,这两个小框分别对应矩阵行等价和列等价,如图中标示的那样;这两个小框之间还有交叠部分,这部分可以理解为两矩阵既可以行等价也可以列等价。换句话说也就是两个矩阵等价的情况,可以是行等价而列不等价;也可以是列等价但是行不等价;还有可能行和列都等价。
矩阵等价的要求是:同一维度就可以了。比如三维矩阵你只要都映射到二维,我们就说矩阵等价。向量组等价的要求是:必须是同一维度的同一空间。比如三维映射到二维就必须映射到同一个平面上。一个映射到 xOz,一个映射到xOy ,我们不说你等价。
 {width=300px}
{width=300px}