向量组的秩与矩阵的秩的关系通俗解释 矩阵的秩 等于 行向量组的秩 等于 列向量组的秩
矩阵的秩反应的是方程组有效的方程的个数,而向量组的秩,反应的是向量组成的空间维度。
从方程理解1 如下一个方程组
{ x 1 + x 2 = 0 2 x 2 + 2 x 2 = 0 \left\{
\begin{array}{c}
x_1 +x_2= 0 \\
2x_2+2 x_2=0
\end{array}
\right. { x 1 + x 2 = 0 2 x 2 + 2 x 2 = 0 ①写出他的系数矩阵,可以得到他的秩为1.
而如果我们从方程看,虽然这里有2个方程,但是第二个方程是第一个方程的2倍,所以,第二个方程是滥竽充数的。因此方程有效的个数是1.
因此,我们得到一个结论:矩阵的秩,本质上反映的是有效方程的个数。详见矩阵的秩
②仍然以上面方程为例,写出向量为 ( 1 , 2 ) (1,2) ( 1 , 2 ) ( 1 , 2 ) (1,2) ( 1 , 2 ) 向量组的等价
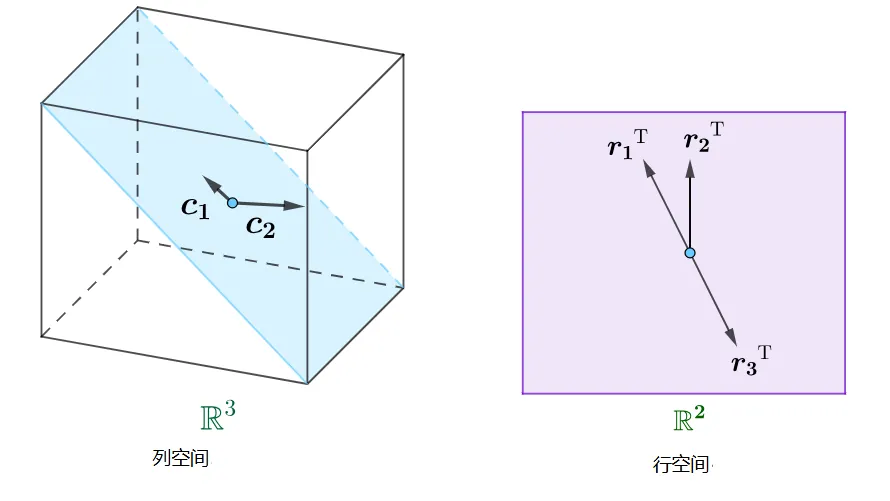
从几何理解2 假设有一个矩阵 A = ( − 1 2 0 2 1 − 2 ) \boldsymbol{A}=\left(\begin{array}{cc}-1 & 2 \\ 0 & 2 \\ 1 & -2\end{array}\right) A = − 1 0 1 2 2 − 2
以列视角看,他有2个列向量,这2个向量张成了一个平面。
以行视角看,他有3个行向量,这3个行向量也张成了一个平面
数学推导 定理 设 A \boldsymbol{A} A m × n m \times n m × n A \boldsymbol{A} A α 1 , α 2 , ⋯ , α n \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n α 1 , α 2 , ⋯ , α n A \boldsymbol{A} A A \boldsymbol{A} A A \boldsymbol{A} A
证明:我们分两步证明这个定理.
(1)先证明,若矩阵 A \boldsymbol{A} A r r r A \boldsymbol{A} A r r r r ( A ) = r r(\boldsymbol{A})=r r ( A ) = r A \boldsymbol{A} A r r r D r ≠ 0 D_r \neq 0 D r = 0 D r D_r D r A \boldsymbol{A} A j 1 , j 2 , ⋯ , j r j_1, j_2, \cdots, j_r j 1 , j 2 , ⋯ , j r
j 1 < j 2 < ⋯ < j r . j_1<j_2<\cdots<j_r . j 1 < j 2 < ⋯ < j r . 由 A \boldsymbol{A} A r r r α j 1 , α j 2 , ⋯ , α j r \boldsymbol{\alpha}_{j_1}, \boldsymbol{\alpha}_{j_2}, \cdots, \boldsymbol{\alpha}_{j_r} α j 1 , α j 2 , ⋯ , α j r A 1 \boldsymbol{A}_1 A 1 r ( A 1 ) = r r\left(\boldsymbol{A}_1\right)=r r ( A 1 ) = r α 1 , α 2 , ⋯ , α m \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m α 1 , α 2 , ⋯ , α m r ( A ) < m r(\boldsymbol{A})<m r ( A ) < m α 1 , α 2 , ⋯ , α m \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m α 1 , α 2 , ⋯ , α m r ( A ) = m r(\boldsymbol{A})=m r ( A ) = m α j 1 , α j 2 , ⋯ , α j r \boldsymbol{\alpha}_{j_1}, \boldsymbol{\alpha}_{j_2}, \cdots, \boldsymbol{\alpha}_{j_r} α j 1 , α j 2 , ⋯ , α j r A \boldsymbol{A} A α j \boldsymbol{\alpha}_j α j r r r
事实上,若 α j \boldsymbol{\alpha}_j α j α j 1 , α j 2 , ⋯ , α j r \boldsymbol{\alpha}_{j_1}, \boldsymbol{\alpha}_{j_2}, \cdots, \boldsymbol{\alpha}_{j_r} α j 1 , α j 2 , ⋯ , α j r α j \boldsymbol{\alpha}_j α j α j 1 , α j 2 , ⋯ , α j \boldsymbol{\alpha}_{j_1}, \boldsymbol{\alpha}_{j_2}, \cdots, \boldsymbol{\alpha}_j α j 1 , α j 2 , ⋯ , α j α j \boldsymbol{\alpha}_j α j α j 1 , α j 2 , ⋯ , α j r \boldsymbol{\alpha}_{j_1}, \boldsymbol{\alpha}_{j_2}, \cdots, \boldsymbol{\alpha}_{j_r} α j 1 , α j 2 , ⋯ , α j r j 1 < j 2 < ⋯ < j i < j < j i + 1 < ⋯ < j r j_1< j_2<\cdots<j_i<j<j_{i+1}<\cdots<j_r j 1 < j 2 < ⋯ < j i < j < j i + 1 < ⋯ < j r
A 2 = ( α j 1 , α j 2 , ⋯ , α j i , α j , α j i + 1 , ⋯ , α j r ) A_2=\left(\alpha_{j_1}, \alpha_{j_2}, \cdots, \alpha_{j_i}, \alpha_j, \alpha_{j_{i+1}}, \cdots, \alpha_{j_r}\right) A 2 = ( α j 1 , α j 2 , ⋯ , α j i , α j , α j i + 1 , ⋯ , α j r ) 是矩阵 A \boldsymbol{A} A r ( A 2 ) ⩽ r ( A ) = r < r + 1 r\left(\boldsymbol{A}_2\right) \leqslant r(\boldsymbol{A})=r<r+1 r ( A 2 ) ⩽ r ( A ) = r < r + 1 α 1 , α 2 , ⋯ , α m \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m α 1 , α 2 , ⋯ , α m r ( A ) < m r(\boldsymbol{A})<m r ( A ) < m α 1 , α 2 , ⋯ , α m \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_m α 1 , α 2 , ⋯ , α m r ( A ) = m r(\boldsymbol{A})=m r ( A ) = m A 2 A_2 A 2 α j \boldsymbol{\alpha}_j α j α j 1 , α j 2 , ⋯ , α j r \boldsymbol{\alpha}_{j_1}, \boldsymbol{\alpha}_{j_2}, \cdots, \boldsymbol{\alpha}_{j_r} α j 1 , α j 2 , ⋯ , α j r
综合(1)(2)可知, α j 1 , α j 2 , ⋯ , α j r \boldsymbol{\alpha}_{j_1}, \boldsymbol{\alpha}_{j_2}, \cdots, \boldsymbol{\alpha}_{j_r} α j 1 , α j 2 , ⋯ , α j r A \boldsymbol{A} A
r ( α 1 , α 2 , ⋯ , α n ) = r = r ( A ) . r\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right)=r=r(\boldsymbol{A}) . r ( α 1 , α 2 , ⋯ , α n ) = r = r ( A ) . 由于 r ( A ) = r ( A T ) r(\boldsymbol{A})=r\left(\boldsymbol{A}^{\mathrm{T}}\right) r ( A ) = r ( A T ) A \boldsymbol{A} A A T \boldsymbol{A}^{\mathrm{T}} A T A \boldsymbol{A} A
r ( A ) = A r(\boldsymbol{A})=\boldsymbol{A} r ( A ) = A = A =\boldsymbol{A} = A
证毕
上述定理的证明过程给出了求向量组的秩及其找一个极大无关组的方法:向量组排成列做成矩阵 A \boldsymbol{A} A r ( A ) = r r(\boldsymbol{A})=r r ( A ) = r r r r A \boldsymbol{A} A r r r r r r r r r A \boldsymbol{A} A r r r A \boldsymbol{A} A
例 设有向量组
α 1 = ( 1 − 2 1 ) , α 2 = ( 2 − 4 2 ) , α 3 = ( 1 0 3 ) , α 4 = ( 0 − 4 − 4 ) , \boldsymbol{\alpha}_1=\left(\begin{array}{r}
1 \\
-2 \\
1
\end{array}\right), \quad \boldsymbol{\alpha}_2=\left(\begin{array}{r}
2 \\
-4 \\
2
\end{array}\right), \quad \boldsymbol{\alpha}_3=\left(\begin{array}{l}
1 \\
0 \\
3
\end{array}\right), \quad \boldsymbol{\alpha}_4=\left(\begin{array}{r}
0 \\
-4 \\
-4
\end{array}\right), α 1 = 1 − 2 1 , α 2 = 2 − 4 2 , α 3 = 1 0 3 , α 4 = 0 − 4 − 4 , 求该向量组的秩和它的一个极大无关组,并将其余向量用所求的极大无关组线性表示。
解:构造矩阵 A = ( α 1 , α 2 , α 3 , α 4 ) \boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_4\right) A = ( α 1 , α 2 , α 3 , α 4 ) A \boldsymbol{A} A
A = ( 1 2 1 0 − 2 − 4 0 − 4 1 2 3 − 4 ) → 初等行变换 ( 1 2 0 2 0 0 1 − 2 0 0 0 0 ) = B . \boldsymbol{A}=\left(\begin{array}{rrrr}
1 & 2 & 1 & 0 \\
-2 & -4 & 0 & -4 \\
1 & 2 & 3 & -4
\end{array}\right) \xrightarrow{\text { 初等行变换 }}\left(\begin{array}{rrrr}
1 & 2 & 0 & 2 \\
0 & 0 & 1 & -2 \\
0 & 0 & 0 & 0
\end{array}\right)=\boldsymbol{B} . A = 1 − 2 1 2 − 4 2 1 0 3 0 − 4 − 4 初等行变换 1 0 0 2 0 0 0 1 0 2 − 2 0 = B . 显然,r ( A ) = r ( B ) = 2 r(\boldsymbol{A})=r(\boldsymbol{B})=2 r ( A ) = r ( B ) = 2 r ( α 1 , α 2 , α 3 , α 4 ) = 2 r\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_4\right)=2 r ( α 1 , α 2 , α 3 , α 4 ) = 2 B \boldsymbol{B} B B = ( β 1 , β 2 , β 3 , β 4 ) \boldsymbol{B}=\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3, \boldsymbol{\beta}_4\right) B = ( β 1 , β 2 , β 3 , β 4 ) β 1 , β 3 \boldsymbol{\beta}_1, \boldsymbol{\beta}_3 β 1 , β 3 B \boldsymbol{B} B A 1 = ( α 1 , α 3 ) \boldsymbol{A}_1=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_3\right) A 1 = ( α 1 , α 3 ) α 1 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_3 α 1 , α 3 A \boldsymbol{A} A
令 α 2 = k 1 α 1 + k 3 α 3 , α 4 = l 1 α 1 + l 3 α 3 \boldsymbol{\alpha}_2=k_1 \boldsymbol{\alpha}_1+k_3 \boldsymbol{\alpha}_3, \boldsymbol{\alpha}_4=l_1 \boldsymbol{\alpha}_1+l_3 \boldsymbol{\alpha}_3 α 2 = k 1 α 1 + k 3 α 3 , α 4 = l 1 α 1 + l 3 α 3 B \boldsymbol{B} B
k 1 = 2 , k 3 = 0 ; l 1 = 2 , l 3 = − 2. k_1=2, k_3=0 ; l_1=2, l_3=-2 . k 1 = 2 , k 3 = 0 ; l 1 = 2 , l 3 = − 2. 所以
α 2 = 2 α 1 , α 4 = 2 α 1 − 2 α 3 . \alpha_2=2 \alpha_1, \quad \alpha_4=2 \alpha_1-2 \alpha_3 . α 2 = 2 α 1 , α 4 = 2 α 1 − 2 α 3 . 提示 值得注意的是 α 2 \boldsymbol{\alpha}_2 α 2 α 1 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_3 α 1 , α 3 α 4 \boldsymbol{\alpha}_4 α 4 α 1 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_3 α 1 , α 3 2 , − 2 2,-2 2 , − 2 B \boldsymbol{B} B α 2 = k 1 α 1 + k 3 α 3 \boldsymbol{\alpha}_2=k_1 \boldsymbol{\alpha}_1+k_3 \boldsymbol{\alpha}_3 α 2 = k 1 α 1 + k 3 α 3 β 2 = k 1 β 1 + k 3 β 3 \boldsymbol{\beta}_2=k_1 \boldsymbol{\beta}_1+k_3 \boldsymbol{\beta}_3 β 2 = k 1 β 1 + k 3 β 3 B \boldsymbol{B} B B \boldsymbol{B} B B \boldsymbol{B} B α 4 = l 1 α 1 + l 3 α 3 \boldsymbol{\alpha}_4= l_1 \boldsymbol{\alpha}_1+l_3 \boldsymbol{\alpha}_3 α 4 = l 1 α 1 + l 3 α 3
更详细解释清参考 向量组的等价
例 设 A , B \boldsymbol{A}, \boldsymbol{B} A , B m × n m \times n m × n
r ( A + B ) ⩽ r ( A ) + r ( B ) . r(\boldsymbol{A}+\boldsymbol{B}) \leqslant r(\boldsymbol{A})+r(\boldsymbol{B}) . r ( A + B ) ⩽ r ( A ) + r ( B ) . 证明:设 A = ( α 1 , α 2 , ⋯ , α n ) \boldsymbol{A}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n\right) A = ( α 1 , α 2 , ⋯ , α n ) B = ( β 1 , β 2 , ⋯ , β n ) \boldsymbol{B}=\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_n\right) B = ( β 1 , β 2 , ⋯ , β n )
A + B = ( α 1 + β 1 , α 2 + β 2 , ⋯ , α n + β n ) . \boldsymbol{A}+\boldsymbol{B}=\left(\boldsymbol{\alpha}_1+\boldsymbol{\beta}_1, \boldsymbol{\alpha}_2+\boldsymbol{\beta}_2, \cdots, \boldsymbol{\alpha}_n+\boldsymbol{\beta}_n\right) . A + B = ( α 1 + β 1 , α 2 + β 2 , ⋯ , α n + β n ) . 再设 A \boldsymbol{A} A B \boldsymbol{B} B
α i 1 , α i 2 , ⋯ , α i s 与 β j 1 , β j 2 , ⋯ , β j t , \boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_s} \text { 与 } \boldsymbol{\beta}_{j_1}, \boldsymbol{\beta}_{j_2}, \cdots, \boldsymbol{\beta}_{j_t} \text {, } α i 1 , α i 2 , ⋯ , α i s 与 β j 1 , β j 2 , ⋯ , β j t , 则矩阵 A \boldsymbol{A} A B \boldsymbol{B} B α i 1 , α i 2 , ⋯ , α i 3 \boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_3} α i 1 , α i 2 , ⋯ , α i 3 β j 1 , β j 2 , ⋯ , β j 1 \boldsymbol{\beta}_{j_1}, \boldsymbol{\beta}_{j_2}, \cdots, \boldsymbol{\beta}_{j_1} β j 1 , β j 2 , ⋯ , β j 1
α p = k 1 α i 1 + k 2 α i 2 + ⋯ + k s α i s β p = l 1 β j 1 + l 2 β j 2 + ⋯ + l t β j t . \begin{gathered}
\boldsymbol{\alpha}_p=k_1 \boldsymbol{\alpha}_{i_1}+k_2 \boldsymbol{\alpha}_{i_2}+\cdots+k_s \boldsymbol{\alpha}_{i_s} \\
\boldsymbol{\beta}_p=l_1 \boldsymbol{\beta}_{j_1}+l_2 \boldsymbol{\beta}_{j_2}+\cdots+l_t \boldsymbol{\beta}_{j_t} .
\end{gathered} α p = k 1 α i 1 + k 2 α i 2 + ⋯ + k s α i s β p = l 1 β j 1 + l 2 β j 2 + ⋯ + l t β j t . 因而
α p + β p = k 1 α i 1 + k 2 α i 2 + ⋯ + k s α i s + l 1 β j 1 + l 2 β j 2 + ⋯ + l t β j t , p = 1 , 2 , ⋯ , n , \boldsymbol{\alpha}_p+\boldsymbol{\beta}_p=k_1 \boldsymbol{\alpha}_{i_1}+k_2 \boldsymbol{\alpha}_{i_2}+\cdots+k_s \boldsymbol{\alpha}_{i_s}+l_1 \boldsymbol{\beta}_{j_1}+l_2 \boldsymbol{\beta}_{j_2}+\cdots+l_t \boldsymbol{\beta}_{j_t}, p=1,2, \cdots, n, α p + β p = k 1 α i 1 + k 2 α i 2 + ⋯ + k s α i s + l 1 β j 1 + l 2 β j 2 + ⋯ + l t β j t , p = 1 , 2 , ⋯ , n , 即矩阵 A + B \boldsymbol{A}+\boldsymbol{B} A + B C = ( α i 1 , α i 2 , ⋯ , α i s , β j 1 , β j 2 , ⋯ \boldsymbol{C}=\left(\boldsymbol{\alpha}_{i_1}, \boldsymbol{\alpha}_{i_2}, \cdots, \boldsymbol{\alpha}_{i_s}, \boldsymbol{\beta}_{j_1}, \boldsymbol{\beta}_{j_2}, \cdots\right. C = ( α i 1 , α i 2 , ⋯ , α i s , β j 1 , β j 2 , ⋯ β j t ) \left.\boldsymbol{\beta}_{j_t}\right) β j t )
r ( A + B ) ⩽ r ( C ) ⩽ s + t = r ( A ) + r ( B ) r(\boldsymbol{A}+\boldsymbol{B}) \leqslant r(\boldsymbol{C}) \leqslant s+t=r(\boldsymbol{A})+r(\boldsymbol{B}) r ( A + B ) ⩽ r ( C ) ⩽ s + t = r ( A ) + r ( B ) 类似地可以证明
max { r ( A ) , r ( B ) } ⩽ r ( A B ) ⩽ r ( A ) + r ( B ) , \max \{r(\boldsymbol{A}), r(\boldsymbol{B})\} \leqslant r(\boldsymbol{A} \boldsymbol{B}) \leqslant r(\boldsymbol{A})+r(\boldsymbol{B}), max { r ( A ) , r ( B )} ⩽ r ( A B ) ⩽ r ( A ) + r ( B ) , 其中 A \boldsymbol{A} A m × p m \times p m × p B \boldsymbol{B} B m × q m \times q m × q ( A , B ) (\boldsymbol{A}, \boldsymbol{B}) ( A , B ) m × ( p + q ) m \times(p+q) m × ( p + q )
例 证明
r ( A B ) ⩽ min { r ( A ) , r ( B ) } , r(\boldsymbol{A B}) \leqslant \min \{r(\boldsymbol{A}), r(\boldsymbol{B})\}, r ( AB ) ⩽ min { r ( A ) , r ( B )} , 其中 A \boldsymbol{A} A m × p m \times p m × p B \boldsymbol{B} B p × n p \times n p × n
A = ( a i j ) m × p = ( α 1 , α 2 , ⋯ , α p ) , B = ( b i j ) p × n , A B = ( γ 1 , γ 2 , ⋯ , γ n ) \boldsymbol{A}=\left(a_{i j}\right)_{m \times p}=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_p\right), \boldsymbol{B}=\left(b_{i j}\right)_{p \times n}, \boldsymbol{A} \boldsymbol{B}=\left(\boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2, \cdots, \boldsymbol{\gamma}_n\right) A = ( a ij ) m × p = ( α 1 , α 2 , ⋯ , α p ) , B = ( b ij ) p × n , A B = ( γ 1 , γ 2 , ⋯ , γ n ) 则
A B = ( γ 1 , γ 2 , ⋯ , γ n ) = ( α 1 , α 2 , ⋯ , α p ) B . A B=\left(\boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2, \cdots, \boldsymbol{\gamma}_n\right)=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_p\right) \boldsymbol{B} . A B = ( γ 1 , γ 2 , ⋯ , γ n ) = ( α 1 , α 2 , ⋯ , α p ) B . 这说明, γ 1 , γ 2 , ⋯ , γ n \boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2, \cdots, \boldsymbol{\gamma}_n γ 1 , γ 2 , ⋯ , γ n α 1 , α 2 , ⋯ , α p \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_p α 1 , α 2 , ⋯ , α p
r ( A B ) = r ( γ 1 , γ 2 , ⋯ , γ n ) ⩽ r ( α 1 , α 2 , ⋯ , α p ) = r ( A ) . r(\boldsymbol{A} \boldsymbol{B})=r\left(\boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2, \cdots, \boldsymbol{\gamma}_n\right) \leqslant r\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_p\right)=r(\boldsymbol{A}) . r ( A B ) = r ( γ 1 , γ 2 , ⋯ , γ n ) ⩽ r ( α 1 , α 2 , ⋯ , α p ) = r ( A ) . 又因为 ( A B ) T = B T A T (\boldsymbol{A} \boldsymbol{B})^{\mathrm{T}}=\boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}} ( A B ) T = B T A T
r ( B T A T ) ⩽ r ( B T ) r\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}\right) \leqslant r\left(\boldsymbol{B}^{\mathrm{T}}\right) r ( B T A T ) ⩽ r ( B T ) 而 r ( B ) = r ( B T ) , r ( A B ) = r ( B T A T ) r(\boldsymbol{B})=r\left(\boldsymbol{B}^{\mathrm{T}}\right), r(\boldsymbol{A B})=r\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}\right) r ( B ) = r ( B T ) , r ( AB ) = r ( B T A T )
r ( A B ) ⩽ r ( B ) r(\boldsymbol{A} \boldsymbol{B}) \leqslant r(\boldsymbol{B}) r ( A B ) ⩽ r ( B ) 因而
r ( A B ) ⩽ min { r ( A ) , r ( B ) } . r(\boldsymbol{A} \boldsymbol{B}) \leqslant \min \{r(\boldsymbol{A}), r(\boldsymbol{B})\} . r ( A B ) ⩽ min { r ( A ) , r ( B )} . 例求向量组 α 1 = ( 1 2 3 0 ) , α 2 = ( − 1 − 1 − 3 1 ) , α 3 = ( 5 0 15 − 10 ) , α 4 = ( − 2 1 − 6 5 ) , α 5 = ( 2 0 5 − 4 ) \alpha _1=\left(\begin{array}{l}1 \\ 2 \\ 3 \\ 0\end{array}\right), \alpha _2=\left(\begin{array}{c}-1 \\ -1 \\ -3 \\ 1\end{array}\right), \alpha _3=\left(\begin{array}{c}5 \\ 0 \\ 15 \\ -10\end{array}\right), \alpha _4=\left(\begin{array}{c}-2 \\ 1 \\ -6 \\ 5\end{array}\right), \alpha _5=\left(\begin{array}{c}2 \\ 0 \\ 5 \\ -4\end{array}\right) α 1 = 1 2 3 0 , α 2 = − 1 − 1 − 3 1 , α 3 = 5 0 15 − 10 , α 4 = − 2 1 − 6 5 , α 5 = 2 0 5 − 4
解 令矩阵
A = ( α 1 , α 2 , α 3 , α 4 , α 5 ) ,对矩阵 A 实施初等行变换化为行最简形矩阵 R : A = ( α 1 , α 2 , α 3 , α 4 , α 5 ) = ( 1 − 1 5 − 2 2 2 − 1 0 1 0 3 − 3 15 − 6 5 0 1 − 10 5 − 4 ) → ( 1 − 1 5 − 2 2 0 1 − 10 5 − 4 0 0 0 0 − 1 0 1 − 10 5 − 4 ) → ( 1 0 − 5 3 0 0 1 − 10 5 0 0 0 0 0 1 0 0 0 0 0 ) = ( β 1 , β 2 , β 3 , β 4 , β 5 ) = R \begin{aligned}
& A =\left( \alpha _1, \alpha _2, \alpha _3, \alpha _4, \alpha _5\right) \text { ,对矩阵 } A \text { 实施初等行变换化为行最简形矩阵 } R \text { :}\\
&A =\left( \alpha _1, \alpha _2, \alpha _3, \alpha _4, \alpha _5\right)=\left(\begin{array}{ccccc}
1 & -1 & 5 & -2 & 2 \\
2 & -1 & 0 & 1 & 0 \\
3 & -3 & 15 & -6 & 5 \\
0 & 1 & -10 & 5 & -4
\end{array}\right) \rightarrow\left(\begin{array}{ccccc}
1 & -1 & 5 & -2 & 2 \\
0 & 1 & -10 & 5 & -4 \\
0 & 0 & 0 & 0 & -1 \\
0 & 1 & -10 & 5 & -4
\end{array}\right) \rightarrow\left(\begin{array}{ccccc}
1 & 0 & -5 & 3 & 0 \\
0 & 1 & -10 & 5 & 0 \\
0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0
\end{array}\right)=\left( \beta _1, \beta _2, \beta _3, \beta _4, \beta _5\right)= R
\end{aligned} A = ( α 1 , α 2 , α 3 , α 4 , α 5 ) ,对矩阵 A 实施初等行变换化为行最简形矩阵 R : A = ( α 1 , α 2 , α 3 , α 4 , α 5 ) = 1 2 3 0 − 1 − 1 − 3 1 5 0 15 − 10 − 2 1 − 6 5 2 0 5 − 4 → 1 0 0 0 − 1 1 0 1 5 − 10 0 − 10 − 2 5 0 5 2 − 4 − 1 − 4 → 1 0 0 0 0 1 0 0 − 5 − 10 0 0 3 5 0 0 0 0 1 0 = ( β 1 , β 2 , β 3 , β 4 , β 5 ) = R 由 R ( R ) = 3 R( R )=3 R ( R ) = 3 R ( A ) = 3. R R( A )=3 . R R ( A ) = 3. R ∣ 1 0 0 0 1 0 0 0 1 ∣ = 1 ≠ 0 \left|\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right|=1 \neq 0 1 0 0 0 1 0 0 0 1 = 1 = 0 β 1 , β 2 , β 5 \beta _1, \beta _2, \beta _5 β 1 , β 2 , β 5 R R R
β 3 = − 5 β 1 − 10 β 2 + 0 ⋅ β 5 , β 4 = 3 β 1 + 5 β 2 + 0 ⋅ β 5 \beta _3=-5 \beta _1-10 \beta _2+0 \cdot \beta _5, \quad \beta _4=3 \beta _1+5 \beta _2+0 \cdot \beta _5 β 3 = − 5 β 1 − 10 β 2 + 0 ⋅ β 5 , β 4 = 3 β 1 + 5 β 2 + 0 ⋅ β 5 由于向量组 α 1 , α 2 , α 3 , α 4 , α 5 \alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5 α 1 , α 2 , α 3 , α 4 , α 5 β 1 , β 2 , β 3 , β 4 , β 5 \beta _1, \beta _2, \beta _3, \beta _4, \beta _5 β 1 , β 2 , β 3 , β 4 , β 5 α 1 , α 2 , α 5 \alpha_1, \alpha_2, \alpha_5 α 1 , α 2 , α 5 α 1 , α 2 , α 3 , α 4 , α 5 \alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5 α 1 , α 2 , α 3 , α 4 , α 5
且有
α 3 = − 5 α 1 − 10 α 2 + 0 ⋅ α 5 , α 4 = 3 α 1 + 5 α 2 + 0 ⋅ α 5 . \alpha _3=-5 \alpha _1-10 \alpha _2+0 \cdot \alpha _5, \quad \alpha _4=3 \alpha _1+5 \alpha _2+0 \cdot \alpha _5 . α 3 = − 5 α 1 − 10 α 2 + 0 ⋅ α 5 , α 4 = 3 α 1 + 5 α 2 + 0 ⋅ α 5 . 在上面的计算里,有些同学可能不太明白表达式的系数是矩阵例值,这不是偶然的,具体原因可以在 极大线性无关性 例2 例解释。
 {width=500px}
{width=500px}