为什么要引入特征值与特征向量 我们在研究线性变换时. 特别关心这样一个问题:对给定线性空间 R n R^n R n R n R^n R n 表示矩阵 ,他具有特别简单的形状 . 比如, 若我们能找到 R n R^n R n { e 1 , e 2 , ⋯ , e n } \left\{e_1, e_2, \cdots, e_n\right\} { e 1 , e 2 , ⋯ , e n } φ \varphi φ
( a 1 a 2 ⋱ a n ) . \left(\begin{array}{llll}
a_1 & & & \\
& a_2 & & \\
& & \ddots & \\
& & & a_n
\end{array}\right) . a 1 a 2 ⋱ a n . 这时, 若 α = k 1 e 1 + k 2 e 2 + ⋯ + k n e n \boldsymbol{\alpha}=k_1 \boldsymbol{e}_1+k_2 \boldsymbol{e}_2+\cdots+k_n \boldsymbol{e}_n α = k 1 e 1 + k 2 e 2 + ⋯ + k n e n
φ ( α ) = a 1 k 1 e 1 + a 2 k 2 e 2 + ⋯ + a n k n e n \boldsymbol{\varphi}(\boldsymbol{\alpha})=a_1 k_1 \boldsymbol{e}_1+a_2 k_2 \boldsymbol{e}_2+\cdots+a_n k_n \boldsymbol{e}_n φ ( α ) = a 1 k 1 e 1 + a 2 k 2 e 2 + ⋯ + a n k n e n 线性变换 φ \varphi φ φ \varphi φ a 1 , a 2 , ⋯ , a r a_1, a_2, \cdots, a_r a 1 , a 2 , ⋯ , a r a r + 1 = ⋯ = a n = 0 a_{r+1}=\cdots=a_n=0 a r + 1 = ⋯ = a n = 0 φ \boldsymbol{\varphi} φ r r r Im φ \operatorname{Im} \boldsymbol{\varphi} Im φ { e 1 , e 2 , ⋯ , e r } \left\{e_1, e_2, \cdots, e_r\right\} { e 1 , e 2 , ⋯ , e r } Ker φ \operatorname{Ker} \varphi Ker φ { e r + 1 , ⋯ , e n } \left\{e_{r+1}, \cdots, e_n\right\} { e r + 1 , ⋯ , e n }
我们已经知道, 一个线性变换在不同基下的表示矩阵是相似的. 因此用矩阵的语言重述上面提到的问题就是: 能否找到一类特别简单的矩阵, 使任一矩阵与这类矩阵中的某一个相似?比如,我们可以问:是否所有的矩阵都相似于对角阵? 若不然, 哪一类矩阵可以相似于对角阵?
在分块矩阵里,我们曾经学过,每一个矩阵都可以按列进行分块,我们自然想到:我们提取矩阵的某一列作为行向量α \alpha α A A A λ \lambda λ A α = λ α A \alpha= \lambda \alpha A α = λ α
从因式分解的角度或许更容易理解特征值与特征向量? 比如,老师让我们求 25 ∗ 12 25 * 12 25 ∗ 12 12 12 12 12 = 4 ∗ 3 12=4 * 3 12 = 4 ∗ 3 25 ∗ 12 = 25 ∗ 4 ∗ 3 = 100 ∗ 3 = 300 25 * 12 = 25 * 4 * 3= 100 *3 =300 25 ∗ 12 = 25 ∗ 4 ∗ 3 = 100 ∗ 3 = 300 25 ∗ 4 = 100 25 * 4 =100 25 ∗ 4 = 100
同样,给我们一个对称矩阵A A A A = P Λ P − 1 A=P \Lambda P^{-1} A = P Λ P − 1
从线性空间角度理解坐标 以经典的 A x = b A x=b A x = b A A A n × n \mathrm{n} \times n n × n x x x b b b n × 1 {n} \times 1 n × 1
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] , x = [ x 1 x 2 ⋮ x n ] , b = [ b 1 b 2 ⋮ b n ] A=\left[\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1 n} \\
a_{21} & a_{22} & \cdots & a_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n 1} & a_{n 2} & \cdots & a_{n n}
\end{array}\right], x=\left[\begin{array}{c}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{array}\right], b=\left[\begin{array}{c}
b_1 \\
b_2 \\
\vdots \\
b_n
\end{array}\right] A = a 11 a 21 ⋮ a n 1 a 12 a 22 ⋮ a n 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a nn , x = x 1 x 2 ⋮ x n , b = b 1 b 2 ⋮ b n 不难看出,矩阵就是由一列列向量组成的,所以在说矩阵之前我们再来简单说一下向量。
向量有长度有方向,但这个长度方向要有意义,或者说可度量,这就必须要有参考系,也就是坐标系。坐标系不是唯一的,但我们有一个标准坐标,叫笛卡尔坐标,简称 I I I
(1)矩阵是一个变换 ,仔细盯着A x = b A x=b A x = b A A A x x x b b b b b b I I I A A A
(2)矩阵本身就是一个坐标系 。这个不难理解,我们常见的 I I I ( 1 , 0 ) , ( 0 , 1 ) (1,0) ,(0,1) ( 1 , 0 ) , ( 0 , 1 )
那一个矩阵乘以一个向量,比如 A x A x A x A A A A A A A A A x x x A A A x x x
A x = [ a 11 a 12 ⋯ ε 1 n a 21 a 22 ⋯ ε 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] [ x 1 x 2 ⋮ x n ] = x 1 [ a 11 a 21 ⋮ a n 1 ] + x 2 [ a 12 a 2 c ⋮ a n 2 ] + ⋯ + x n [ a 1 n a 2 n ⋮ a n n ] \begin{aligned}
& A x=\left[\begin{array}{cccc}
a_{11} & a_{12} & \cdots & \varepsilon_{1 n} \\
a_{21} & a_{22} & \cdots & \varepsilon_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n 1} & a_{n 2} & \cdots & a_{n n}
\end{array}\right]\left[\begin{array}{c}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{array}\right]=x_1\left[\begin{array}{c}
a_{11} \\
a_{21} \\
\vdots \\
a_{n 1}
\end{array}\right]+x_2\left[\begin{array}{c}
a_{12} \\
a_{2 c} \\
\vdots \\
a_{n 2}
\end{array}\right]+\cdots
& +x_n\left[\begin{array}{c}
a_{1 n} \\
a_{2 n} \\
\vdots \\
a_{n n}
\end{array}\right]
\end{aligned} A x = a 11 a 21 ⋮ a n 1 a 12 a 22 ⋮ a n 2 ⋯ ⋯ ⋱ ⋯ ε 1 n ε 2 n ⋮ a nn x 1 x 2 ⋮ x n = x 1 a 11 a 21 ⋮ a n 1 + x 2 a 12 a 2 c ⋮ a n 2 + ⋯ + x n a 1 n a 2 n ⋮ a nn 我们再来看 A x = b A x=b A x = b b b b I I I b b b I I I A x = I b A x=I b A x = I b A x A x A x A A A x , I b x , I b x , I b I I I b b b x x x b b b
来看个数学上的例子
A = [ 1 − 1 1 1 ] , x = [ 2 1 ] , I = [ 1 0 0 1 ] , b = [ 1 3 ] A=\left[\begin{array}{cc}
1 & -1 \\
1 & 1
\end{array}\right], x=\left[\begin{array}{l}
2 \\
1
\end{array}\right], I=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right], b=\left[\begin{array}{l}
1 \\
3
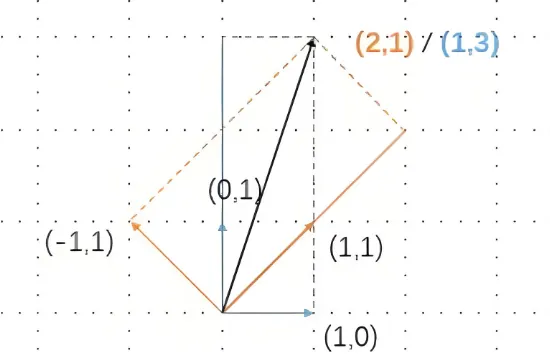
\end{array}\right] A = [ 1 1 − 1 1 ] , x = [ 2 1 ] , I = [ 1 0 0 1 ] , b = [ 1 3 ] 如果你计算,你会发现上面这个矩阵乘法 A x = I b = b Ax=Ib=b A x = I b = b ( 2 , 1 ) (2,1) ( 2 , 1 ) ( 1 , 3 ) (1,3) ( 1 , 3 ) A A A I I I
再看一个简单的类比,
( 5 ) ∗ 1 = 5 ∗ 1 (5)*1=5*1 ( 5 ) ∗ 1 = 5 ∗ 1 ( 5 ) (5) ( 5 ) 5 5 5 ( 5 ) ∗ 2 = 10 ∗ 1 (5)*2=10*1 ( 5 ) ∗ 2 = 10 ∗ 1
上式还可以简单类比,一件东西需要10元钱,我以1元人民币为单位,给他10次就可以了。但是我也可以以5元人民币为单位,只要给他2次就可以了。
通过物理对上面进行解释 在高中学过运动,比如:甲在路边,乙在飞船上,一辆汽车以v 汽 v_汽 v 汽 A A A v A v_A v A 这里的参照物可以理解为线性代数里的基坐标 )。比如甲在地面上,以地面为参照物,v A = v 汽 + v A − 汽 v_A=v_\text{汽} +v_{A-\text{汽}} v A = v 汽 + v A − 汽 v A = v 飞船 + v 汽-船 + v A − 汽 v_A=v_{\text{飞船}} + v_\text{汽-船} +v_{A-\text{汽}} v A = v 飞船 + v 汽 - 船 + v A − 汽
再仔细的盯着上面这张图(如下)
现在把上图想象为物体的运动:蓝色单位坐标系 ( 1 , 0 0 , 1 ) \left(\begin{array}{cc}1,0 \\0,1\end{array} \right) ( 1 , 0 0 , 1 ) 宇宙飞船 ,他的单位坐标系是( − 1 , 1 1 , 1 ) \left(\begin{array}{cc}-1,1 \\1,1\end{array} \right) ( − 1 , 1 1 , 1 )
在蓝色坐标系里,甲看到的汽车运动速度( 1 , 3 ) (1,3) ( 1 , 3 ) ( 2 , 1 ) (2,1) ( 2 , 1 )
现在的问题是:我们能否把橙色坐标系里的运动,都用类蓝色坐标系表示,为何?因为简单 。比如上图里,假设蓝色坐标系里看到的汽车速度为( 5 , 7 ) (5,7) ( 5 , 7 ) x x x y y y A A A A = B C D A=BCD A = BC D B B B
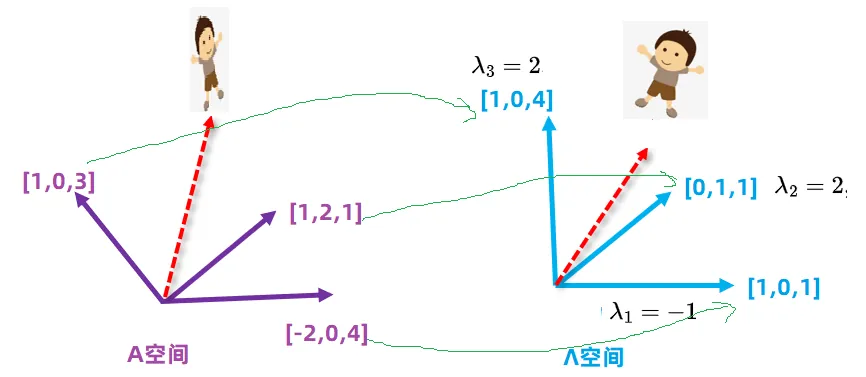
特征值与特征向量的设计 在找寻特征向量的过程其实就是找寻新的坐标基的过程 ,如何寻找呢?矩阵作用与向量,通常使得向量旋转和缩放,但是在这些方向里,有一些向量只缩放,不旋转,那么我们就使用那种不旋转的向量作为新的坐标基 。但是有一个大前提,对于一个n n n n n n A = ( − 2 1 1 0 2 0 − 4 1 3 ) A=\left(\begin{array}{lll}-2 & 1 & 1 \\0 & 2 & 0 \\-4 & 1 & 3 \end{array}\right) A = − 2 0 − 4 1 2 1 1 0 3 Λ = ( 1 0 1 0 1 0 1 1 4 ) \Lambda=\left(\begin{array}{lll}1 & 0 & 1 \\0 & 1 & 0 \\1 & 1 & 4 \end{array}\right) Λ = 1 0 1 0 1 1 1 0 4 A A A Λ \Lambda Λ
因为小男孩的移动最多可以沿着x , y , z x,y,z x , y , z
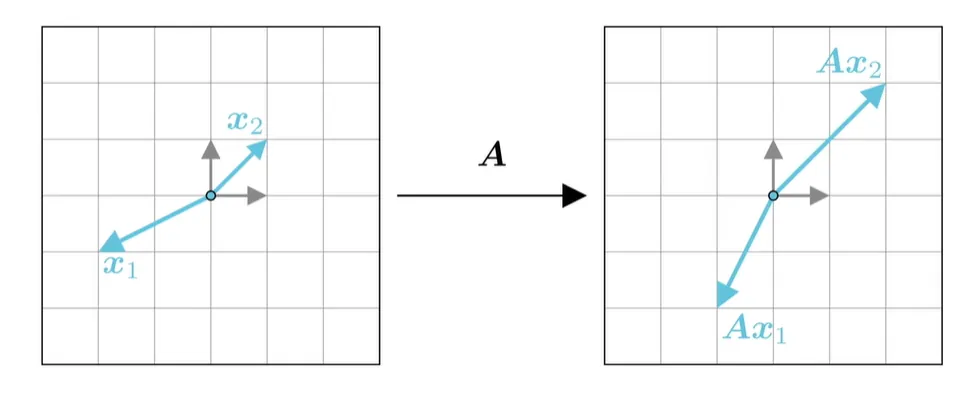
矩阵作用于向量的具体实现 上面说过,一个矩阵A A A x 1 \boldsymbol{x_1} x 1 A A A x 1 → A x 1 \boldsymbol{x_1} \to A \boldsymbol{x_1} x 1 → A x 1
但是,也有部分向量,只进行了缩放,而不进行旋转,如下图 x 2 → A x 2 \boldsymbol{x_2} \to A \boldsymbol{x_2} x 2 → A x 2
既然 x 2 \boldsymbol{x_2} x 2 x 2 → λ x 2 \boldsymbol{x_2} \to \lambda \boldsymbol{x_2} x 2 → λ x 2
因此,我们只要令 A x 2 = λ x 2 A \boldsymbol{x_2}= \lambda \boldsymbol{x_2} A x 2 = λ x 2 λ \lambda λ x 2 \boldsymbol{x_2} x 2
注意:如果A A A A A A A A T AA^T A A T
特征值与特征向量的定义 数学上定义当 A x = λ x A x=\lambda x A x = λ x x x x A A A λ \lambda λ A A A 事实上,这里的x x x
我们用坐标系的角度来理解,那么 A x = λ x A x=\lambda x A x = λ x A A A x x x I I I x x x λ \lambda λ
举一个例子,
A = [ 3 1 2 2 ] , λ = 4 , α 1 = [ 1 1 ] , α 2 = [ 1 2 ] A=\left[\begin{array}{cc}
3 & 1 \\
2 & 2
\end{array}\right],
\lambda=4,
\alpha_1=\left[\begin{array}{ll}
1 \\
1
\end{array}\right],
\alpha_2=\left[\begin{array}{l}
1 \\
2
\end{array}\right] A = [ 3 2 1 2 ] , λ = 4 , α 1 = [ 1 1 ] , α 2 = [ 1 2 ] 计算得到
A α 1 = [ 3 1 2 2 ] [ 1 1 ] = [ 4 4 ] = 4 α 1 A \alpha_1=\left[\begin{array}{cc}
3 & 1 \\
2 & 2
\end{array}\right] \left[\begin{array}{ll}
1 \\
1
\end{array}\right]=\left[\begin{array}{ll}
4 \\
4
\end{array}\right]=4 \alpha_1 A α 1 = [ 3 2 1 2 ] [ 1 1 ] = [ 4 4 ] = 4 α 1 A α 2 = [ 3 1 2 2 ] [ 1 2 ] = [ 5 6 ] ≠ 4 α 2 A \alpha_2=\left[\begin{array}{cc}
3 & 1 \\
2 & 2
\end{array}\right] \left[\begin{array}{ll}
1 \\
2
\end{array}\right]=\left[\begin{array}{ll}
5 \\
6
\end{array}\right] \ne 4 \alpha_2 A α 2 = [ 3 2 1 2 ] [ 1 2 ] = [ 5 6 ] = 4 α 2 从这个计算里可以看到,α 1 \alpha_1 α 1 4 4 4 α 2 \alpha_2 α 2 α 1 \alpha_1 α 1
如果A A A A A A
对角形矩阵 只有主对角线还有元素,其余都是0的矩阵,是对角型矩阵,下面是一个二阶对角矩阵:
A = [ 2 0 0 10 ] A=\left[\begin{array}{cc}
2 & 0 \\
0 & 10
\end{array}\right] A = [ 2 0 0 10 ] 它互相独立的标准化特征向量有 2 个,
x 1 = [ 1 0 ] , x 2 = [ 0 1 ] x_1=\left[\begin{array}{l}
1 \\
0
\end{array}\right], x_2=\left[\begin{array}{l}
0 \\
1
\end{array}\right] x 1 = [ 1 0 ] , x 2 = [ 0 1 ] 他们的特征值分别是 2 2 2 10 10 10
可以看到,如果一个矩阵是对角形矩阵,他们可以直接使用单位矩阵E E E A A A A A A x x x y y y z z z
如下图,在上面说过,一个矩阵就相当于一个坐标系单位(注意不是坐标系里向量的值),既然 笛卡尔坐标系 ( 1 , 0 0 , 1 ) \left(\begin{array}{cc}1,0 \\0,1\end{array} \right) ( 1 , 0 0 , 1 )
那一个向量它在 I I I ( 1 , 1 ) (1,1) ( 1 , 1 ) A A A ( 2 , 10 ) (2,10) ( 2 , 10 ) ( 1 , 1 ) (1, 1) ( 1 , 1 ) ( 2 , 10 ) (2,10) ( 2 , 10 )
我们把( 1 , 1 ) (1,1) ( 1 , 1 ) 1 , 0 1,0 1 , 0 0 , 1 0,1 0 , 1 ( 2 , 10 ) (2,10) ( 2 , 10 ) ( 2 , 0 ) (2,0) ( 2 , 0 ) ( 0 , 10 ) (0,10) ( 0 , 10 )
这样,只要把水平方向扩大2倍,垂直方向扩大10倍,就可以把 ( 1 , 1 ) (1,1) ( 1 , 1 ) ( 2 , 10 ) (2,10) ( 2 , 10 ) 2 2 2 10 10 10 特征值 ,而对应的( 1 , 0 ) (1,0) ( 1 , 0 ) ( 0 , 1 ) (0,1) ( 0 , 1 ) 特征向量 。
特别的,我们把2,10叫做 矩阵的迹 ,他描述的是线性变换本身固有的、独立于所选择基底的属性。无论你用什么坐标系来描述同一个线性变换,它的迹是不变性 。
到这里可以发现,如果一个矩阵能化为对角形矩阵,那么只要以主对角线为坐标单位,就可以很容易化为标准坐标系。而主对角线里的值正好是矩阵的特征值。
对角矩阵的好处 再看一个例子,如果一个变换可以写成对角矩阵,那么它的特征值就是它对角线上的元素,而特征向量就是相应的基。例如矩阵:
A = [ 2 0 0 0 2 0 0 0 4 ] A =\left[\begin{array}{lll}2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 4\end{array}\right] A = 2 0 0 0 2 0 0 0 4 ( a , b , 0 ) T (a, b, 0)^T ( a , b , 0 ) T ( 0 , 0 , c ) T (0,0, c)^T ( 0 , 0 , c ) T A A A { 2 , 4 } \{2,4\} { 2 , 4 }
普通矩阵的相似 我们定义
P − 1 A P = B . . . ( 1 ) \boxed{
P^{-1} A P= B ...(1)
} P − 1 A P = B ... ( 1 ) 则称呼A A A B B B 矩阵相似 ,如果把(1)稍微变形一下,左乘P P P P − 1 P^{-1} P − 1
A = P B P − 1 . . . ( 2 ) \boxed{
A=PBP^{-1}...(2)
} A = PB P − 1 ... ( 2 ) 这表明一个矩阵A A A 矩阵相似的几何意义
普通矩阵的的对角化 上面(2)式表明一个矩阵可以分解为三个矩阵,现在我们“得寸进尺”提高要求,我们希望这里的B B B
A = P Λ P − 1 . . . ( 3 ) \boxed{
A=P\Lambda P^{-1}...(3)
} A = P Λ P − 1 ... ( 3 ) 就像因式分解一样,假设矩阵A A A Λ \Lambda Λ A 3 A^3 A 3 A = P Λ P − 1 A = P \Lambda P ^{-1} A = P Λ P − 1
A 3 = P Λ P − 1 ⋅ P Λ P − 1 ⋅ P Λ P − 1 A^3 = P \Lambda P ^{-1} \cdot P \Lambda P ^{-1} \cdot P \Lambda P ^{-1} A 3 = P Λ P − 1 ⋅ P Λ P − 1 ⋅ P Λ P − 1 再利用结合律,即得
A 3 = P Λ 3 P − 1 A^3 = P \Lambda^3 P ^{-1} A 3 = P Λ 3 P − 1 这样计算A 3 A^3 A 3 此处 例子。
现在假如(3)式已经实现, 左乘P − 1 P^{-1} P − 1 P P P
P − 1 A P = Λ . . . ( 4 ) \boxed{
P^{-1} A P= \Lambda ...(4)
} P − 1 A P = Λ... ( 4 ) 我们称矩阵A A A 。
其实,对于(4)式,对普通矩阵还真没多大使用价值。但是,如果这个普通矩阵又是对称矩阵,就立刻发挥他强大的价值,利用对称矩阵的特征值相当于给我们找到了一个正交矩阵,这里最重要的一个结论是:对称矩阵的特征向量是互相垂直的 。
特征分解(Eigendecomposition) 对于(3)式,即
A = P Λ P − 1 \boxed{A = P \Lambda P ^{-1}} A = P Λ P − 1 可以看到矩阵A变成三个矩阵相乘的形式,我们称呼这种乘法为:特征分解。特征分解揭示了矩阵 A 的内在缩放特性。它表明矩阵 A 对向量的作用可以分解为:先将向量转换到特征向量定义的坐标系下,特征向量就是这个新坐标系的基底,然后在各个特征向量方向上进行缩放,最后再转换回原始坐标系。
从几何上理解特征值与特征向量 在上面介绍了特征值与特征向量,这里进一步从广义的视角介绍其集合意义。
方阵乘以一个向量的结果仍是一个同维向量, 矩阵乘法对应了一个变换, 把一个向量变成同维数的另一个向量。在这个变换的过程中, 向量会发生旋转、伸缩或镜像的变化。矩阵不同,向量变化的结果也会不同。如果矩阵对某一个向量或某些向量只发生伸缩变换, 不对这些向量产生旋转效果, 那么这些向量就是这个矩阵的特征向量 , 伸缩的比例就是特征值; 如果伸缩的比例值是负值, 原向量的方向改变为反方向, 原向量仍然是这个矩阵的特征向量。
比如二维逆时针旋转 π / 2 \pi / 2 π /2 π / 2 \pi / 2 π /2
再返回来盯着特征向量的定义 “ A a = λ a \boldsymbol{A a}=\boldsymbol{\lambda} \boldsymbol{a} Aa = λ a A \boldsymbol{A} A ⋯ ⋯ ⋅ \cdots \cdots \cdot ⋯⋯ ⋅ λ a \lambda \boldsymbol{a} λ a A \boldsymbol{A} A a \boldsymbol{a} a λ a \lambda \boldsymbol{a} λ a a \boldsymbol{a} a λ \lambda λ a \boldsymbol{a} a
例如, 设某矩阵 A \boldsymbol{A} A a = ( − 1 1 ) 、 b = ( 2 1 ) \boldsymbol{a}=\left(\begin{array}{c}-1 \\ 1\end{array}\right) 、 \boldsymbol{b}=\left(\begin{array}{l}2 \\ 1\end{array}\right) a = ( − 1 1 ) 、 b = ( 2 1 ) a ′ = A a = ( − 5 − 1 ) \boldsymbol{a}^{\prime}=\boldsymbol{A} \boldsymbol{a}=\left(\begin{array}{l}-5 \\ -1\end{array}\right) a ′ = A a = ( − 5 − 1 ) b ′ = A b = ( 4 2 ) \boldsymbol{b}^{\prime}=\boldsymbol{A} \boldsymbol{b}=\left(\begin{array}{l}4 \\ 2\end{array}\right) b ′ = A b = ( 4 2 ) b \boldsymbol{b} b A \boldsymbol{A} A A b = 2 b \boldsymbol{A} \boldsymbol{b}=2 \boldsymbol{b} A b = 2 b b \boldsymbol{b} b A \boldsymbol{A} A
对于矩阵 A \boldsymbol{A} A a \boldsymbol{a} a A a = λ a \boldsymbol{A} \boldsymbol{a}=\boldsymbol{\lambda} \boldsymbol{a} A a = λ a a \boldsymbol{a} a a \boldsymbol{a} a A a \boldsymbol{A} \boldsymbol{a} A a a \boldsymbol{a} a λ \lambda λ A \boldsymbol{A} A
因此, 从矩阵的几何意义来看, 矩阵 A \boldsymbol{A} A a \boldsymbol{a} a A \boldsymbol{A} A A \boldsymbol{A} A λ \lambda λ a \boldsymbol{a} a
从代数的角度看特征值与特征向量 定义一个算子 T ∈ R 3 T \in R^3 T ∈ R 3 ( x , y , z ) ∈ R 3 (x, y, z) \in R ^3 ( x , y , z ) ∈ R 3
T ( x , y , z ) = ( 7 x + 3 z , 3 x + 6 y + 9 z , − 6 y ) . T(x, y, z)=(7 x+3 z, 3 x+6 y+9 z,-6 y) . T ( x , y , z ) = ( 7 x + 3 z , 3 x + 6 y + 9 z , − 6 y ) . 那么 T ( 3 , 1 , − 1 ) = ( 18 , 6 , − 6 ) = 6 ( 3 , 1 , − 1 ) T(3,1,-1)=(18,6,-6)=6(3,1,-1) T ( 3 , 1 , − 1 ) = ( 18 , 6 , − 6 ) = 6 ( 3 , 1 , − 1 ) T T T
总结 前面说,矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
实际上,上述的一段话既讲了矩阵变换特征值及特征向量的几何意义(图形变换),也讲了其物理含义。物理含义就是运动的图景:特征向量在一个矩阵的作用下作伸缩运动,伸缩的幅度由特征值确定。特征值大于 1 ,所有属于此特征值的特征向量身形暴长;特征值大于 0 小于 1 ,特征向量身形猛缩;特征值小于 0 ,特征向量缩过了界,反方向到 0 点那边去了。
关于特征值和特征向量,这里请注意两个亮点:一个是线性不变量的含义,一个是振动的谱含义。
1.特征向量是线性不变量
有一个著名的布劳维尔(Brouwer)不动点定理,在经济分析中常用于求解市场均衡点的问题。不动点就是一种不变量。不动点的定义如下:
设 σ : M → M \sigma: M \rightarrow M σ : M → M M M M x ∗ ∈ M x^* \in M x ∗ ∈ M
σ ( x ∗ ) = x ∗ \sigma\left(x^*\right)=x^* σ ( x ∗ ) = x ∗ 则称 x ∗ x ^* x ∗ σ \sigma σ
我们现在讲的线性变换或矩阵变换同样具有不动点的概念。线性空间里的元素 x x x x x x λ x ∗ \lambda \boldsymbol { x } ^ { * } λ x ∗
σ ( x ∗ ) = λ x ∗ \sigma\left(x^*\right)=\lambda x^* σ ( x ∗ ) = λ x ∗ ( λ \lambda λ σ \sigma σ
不过,我们参考上节的引例 理解-凸透镜成像原理理解不变量的意义
2.特征值是振动的谱
在理解关于振动的特征值和特征向量的过程中,需要加入复特征值或复向量抑或复矩阵的概念,因为在实际应用中实特征值们是干不了多少事的。机械振动和电振动有频谱,振动的某个频率具有某个幅度,那么矩阵也有矩阵的谱,矩阵的谱就是矩阵特征值的概念,是矩阵所固有的特性,所有的特征值形成了矩阵的一个频谱,每个特征值是矩阵的一个 "谐振频点"。
美国数学家斯特朗(G.Strang)在其经典教材《线性代数及其应用》中这样介绍了特征值作为频率的物理意义,他说:
大概最简单的例子(我从不相信其真实性,虽然据说 1831 年有一桥梁毁于此因)是一对士兵通过桥梁的例子。传统上,他们要停止齐步前进而要散步通过。这个理由是因为他们可能以等于桥的特征值之一的频率齐步行进,从而将发生共振。就像孩子的秋千那样,你一旦注意到一个秋千的频率,和此频率相配,你就使频率荡得更高。一个工程师总是试图使他的桥梁或他的火箭的自然频率远离风的频率或液体燃料的频率;而在另一种极端情况,一个证券经纪人则尽毕生精力与努力到达市场的自然频率线。特征值是几乎任何一个动力系统的最重要的特征。
其实,这个矩阵之所以能形成"频率的谱",就是因为矩阵在特征向量所指的方向上具有对向量产生恒定的变换作用:周期性地增强(或减弱)特征向量的作用。进一步地,如果矩阵持续地叠代作用于向量,那么特征向量就会凸现出来。
在《线性代数的几何意义》里,作者说,一个线性物理系统,其特性可以被一个矩阵所描述,那么这个系统的物理特性就可以被这个矩阵的特征值所决定,各种不同的信号(向量)进入这个系统中后,系统输出的信号 (向量)就会发生相位超前或滞后、幅度放大或缩小等各种纷乱的变化。但只有特征信号(特征向量)被稳定地发生放大(或缩小)的变化。如果把系统的输出端口接入输入端口,那么只有特征信号(特征向量)第二次被放大(或缩小)了,其他信号继续其纷乱的不稳定变化幅度得不到增强……经过 n n n
 {width=300px}
{width=300px}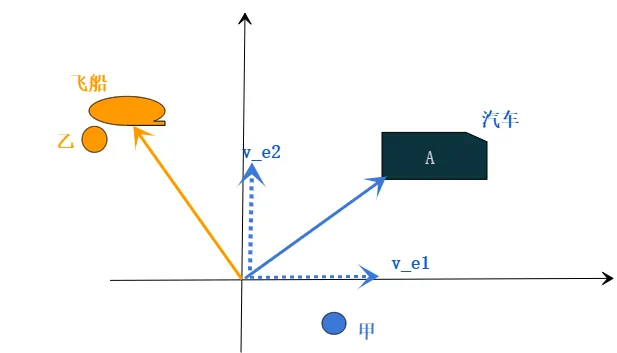 {width=380px}
{width=380px}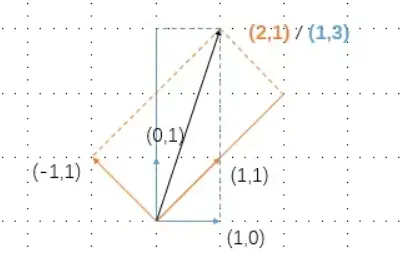
 {width=500px}
{width=500px}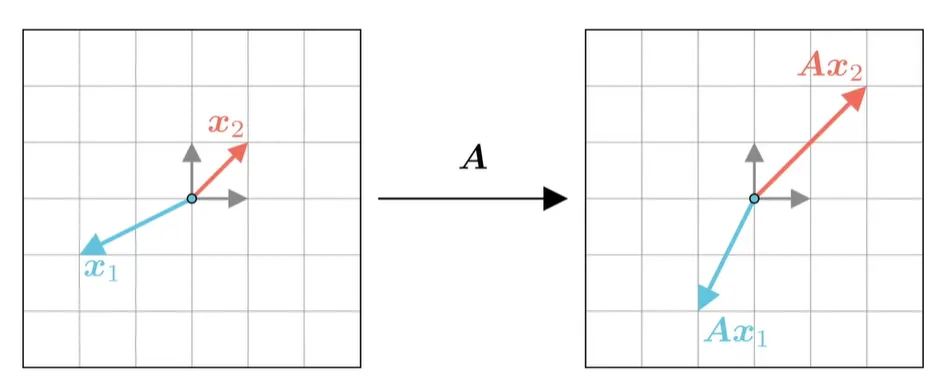 {width=500px}
{width=500px}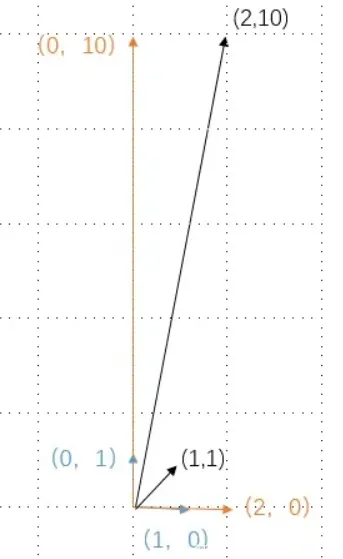 {width=200px}
{width=200px}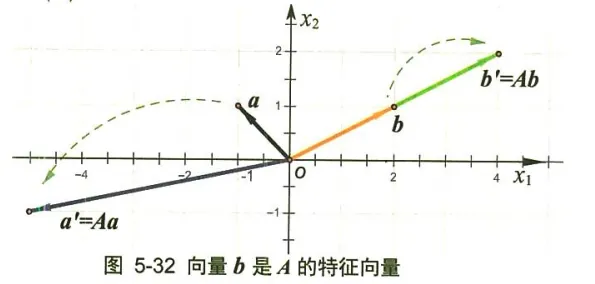 显然, 只有向量 被矩阵 同方向拉长了 2 倍, 即 , 因此向量 是矩阵 的特征向量, 特征值为 2 。
显然, 只有向量 被矩阵 同方向拉长了 2 倍, 即 , 因此向量 是矩阵 的特征向量, 特征值为 2 。